04-矩阵乘法与线性变换复合

据我的经验，如果丢掉矩阵的话，那些涉及矩阵的证明可以缩短一半。

​ —埃尔米‧阿廷

线性变换复合

• 很多时候你会发现你想描述这样一种作用：进行一个变换之后再进行另一个变换

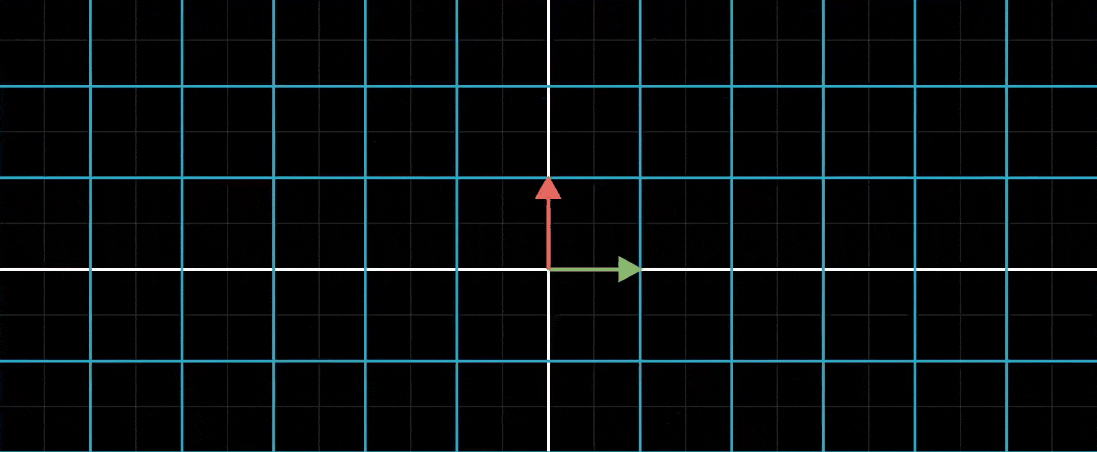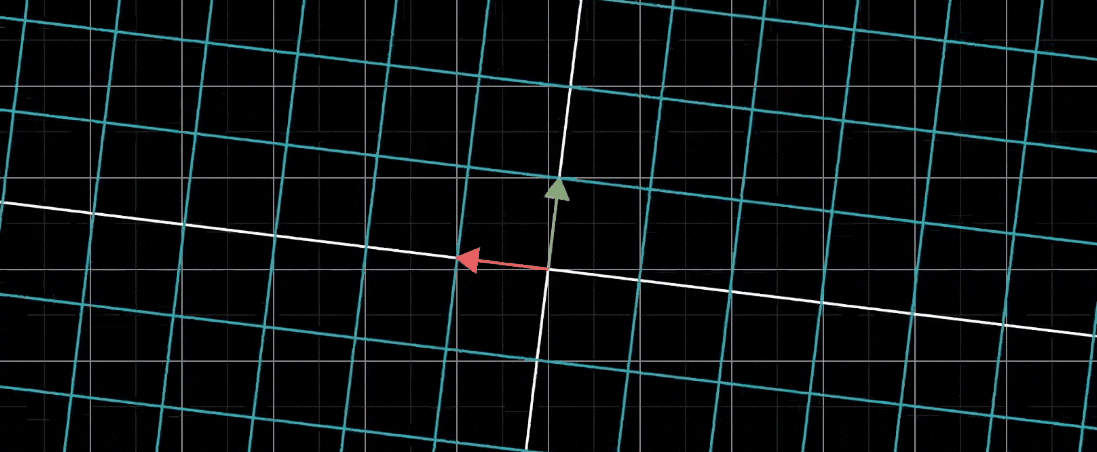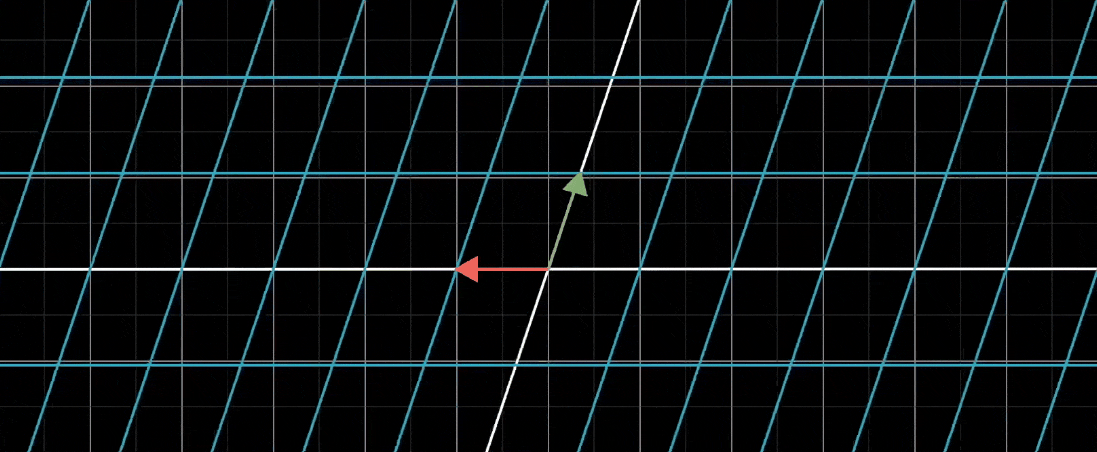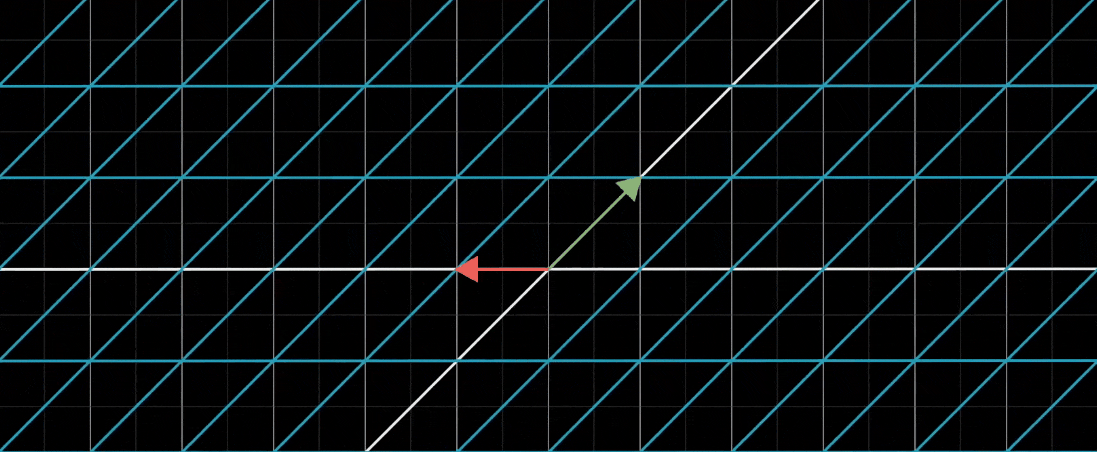
• 比如说，你想描述将整个平面逆时针旋转90度后，再进行一次剪切变换会发生什么

• 从头到尾的总体作用是另一个线性变换，它和旋转和剪切明显不同。这个新的线性变换通常被称为前两个独立变换的 “复合变换”

• 和其他线性变换一样，我们也能通过追踪i帽和j帽，并用矩阵完全描述这个复合变换

• 在这个例子中，i帽在两个线性变换之后的最终落点是（1，1），我们将它作为矩阵的第一列；类似地，j帽最终落在（-1，0），我们将它作为矩阵的第二列

• 这一新的矩阵捕捉到了旋转然后剪切的总体效应，但它是一个单独的作用，而不是两个相继作用的合成

• 这里有种方法来考虑这个新矩阵，如果你有一个向量，将它进行旋转然后剪切，一个麻烦的计算方法是：首先将它左乘旋转矩阵，然后将得到的结果再左乘剪切矩阵。从数值角度看，这意味着对一个给定向量进行旋转然后剪切。但是无论所选向量是什么，结果都应该与复合变换作用的结果完全相同，因为新矩阵应当捕捉到了旋转然后剪切的相同总体效应

• 根据这里写下的内容，可以认为将这个新矩阵称为最初两个矩阵的积是合理的

时刻记得，两个矩阵相乘有着几何意义，也就是两个线性变换相继作用

注意，这个乘积需要从右向左读，首先应用右侧矩阵所描述的变换，然后再应用左侧矩阵所描述的变换。它起源于函数的记号，因为我们将函数写在变量左侧，所以每次将两个函数复合时，总是要从右向左读

矩阵乘法

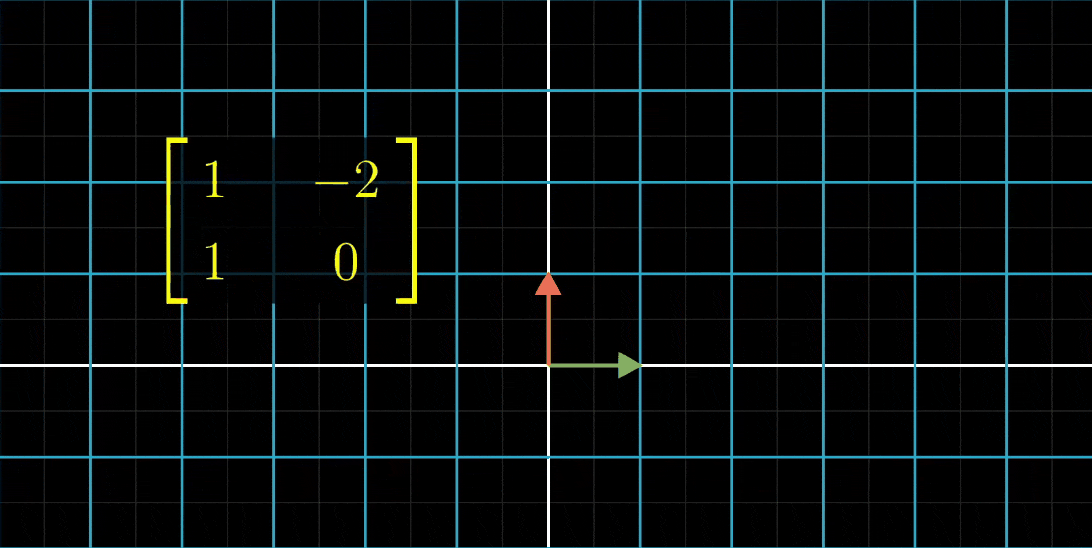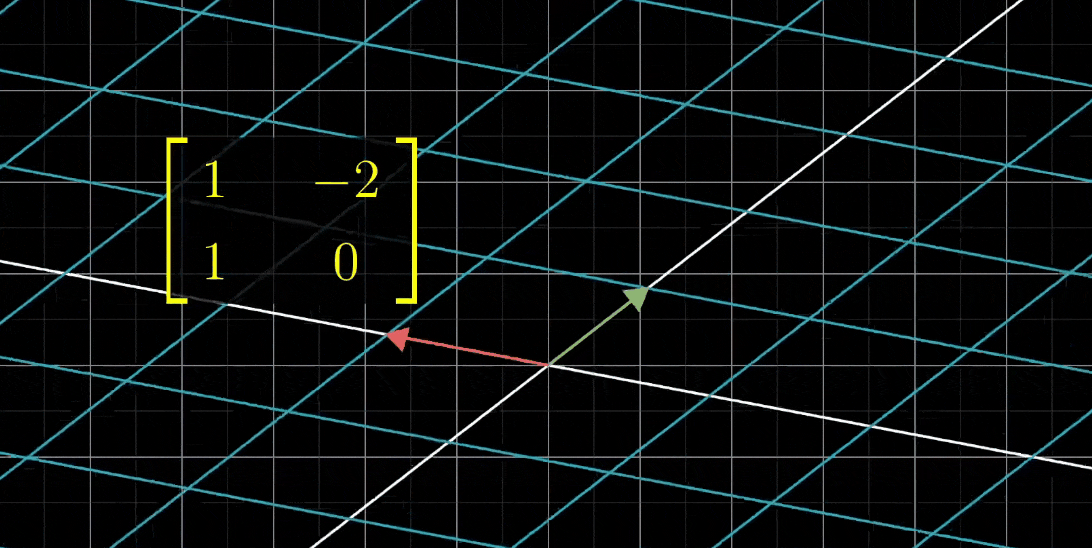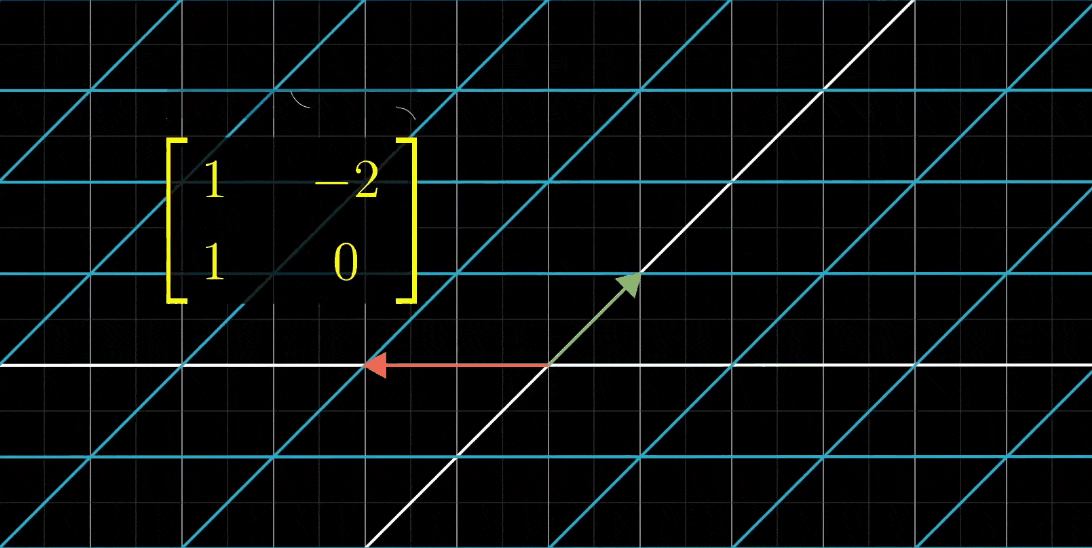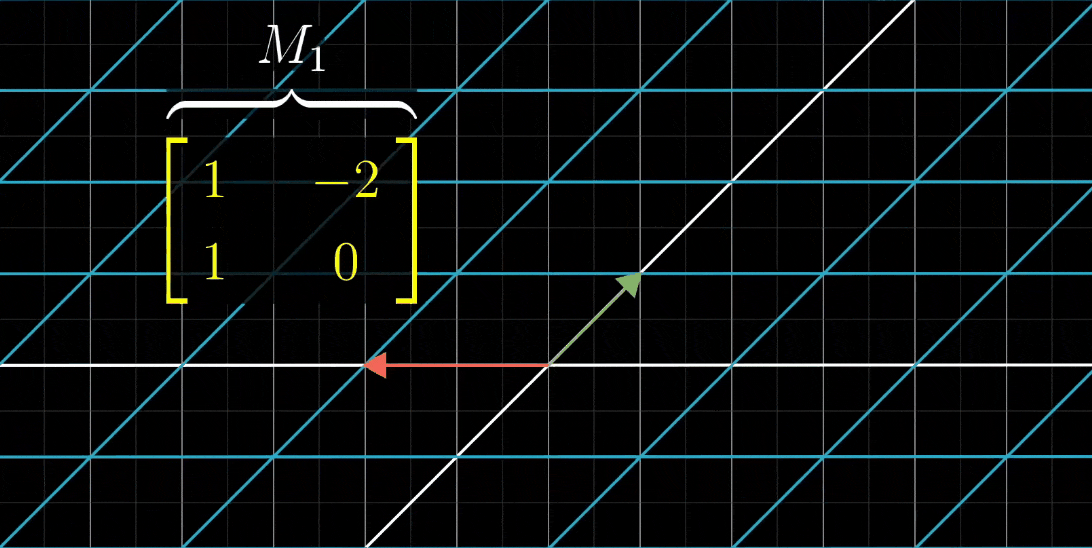
• 我们再看一个例子，两列为（1，1）和（-2，0）它所代表的变换长这样，我们称它为M1

• 另一个矩阵，两列为（0，1）和（2，0），它所代表的变换长这样，我们称它为M2

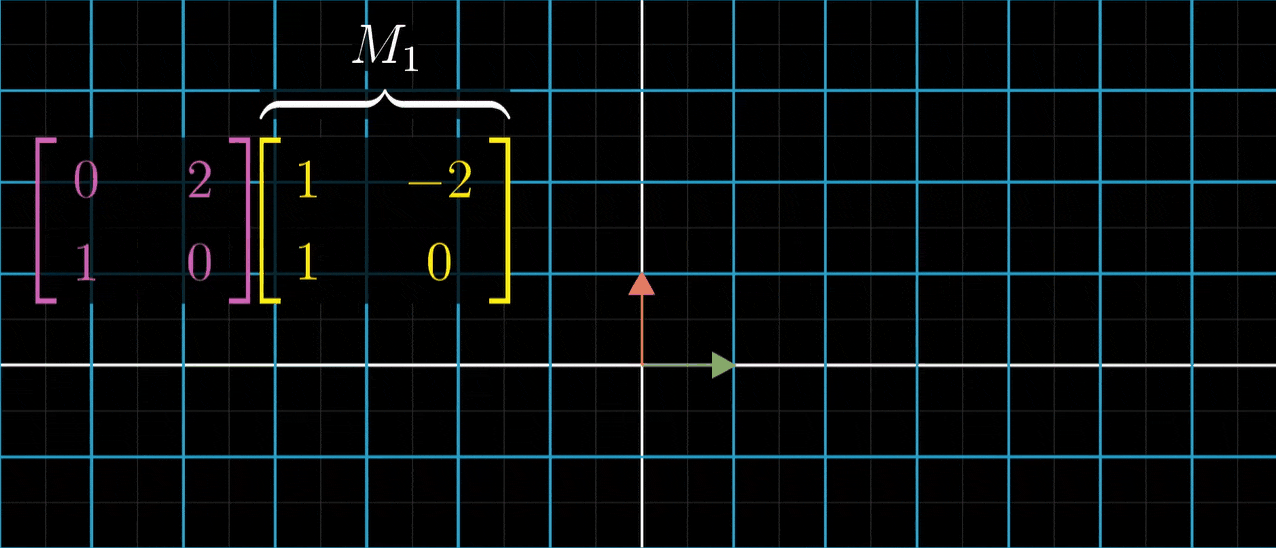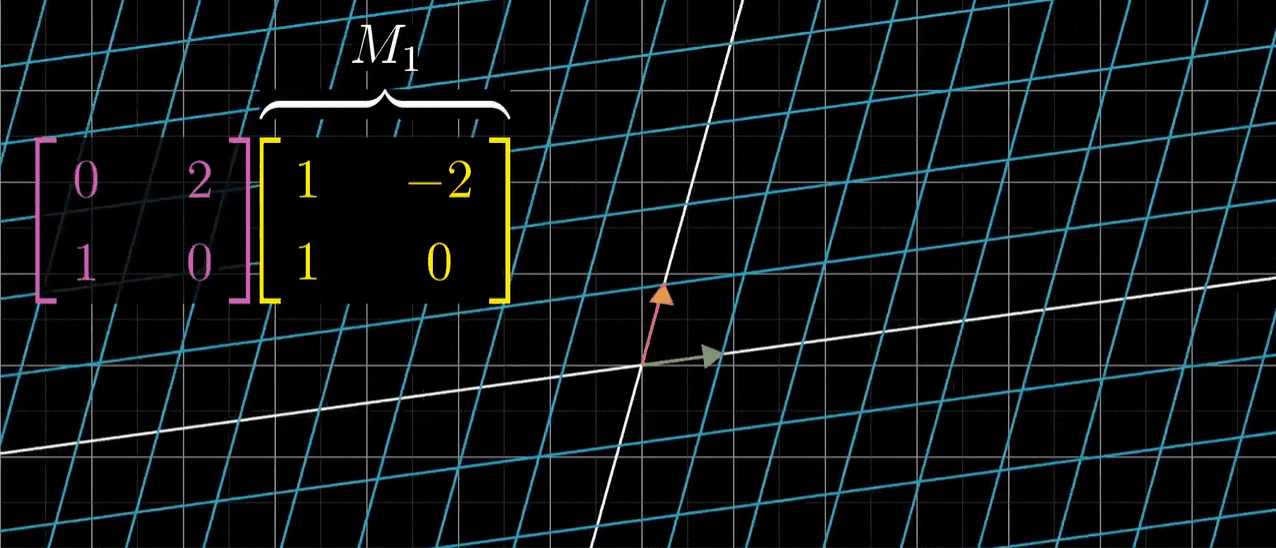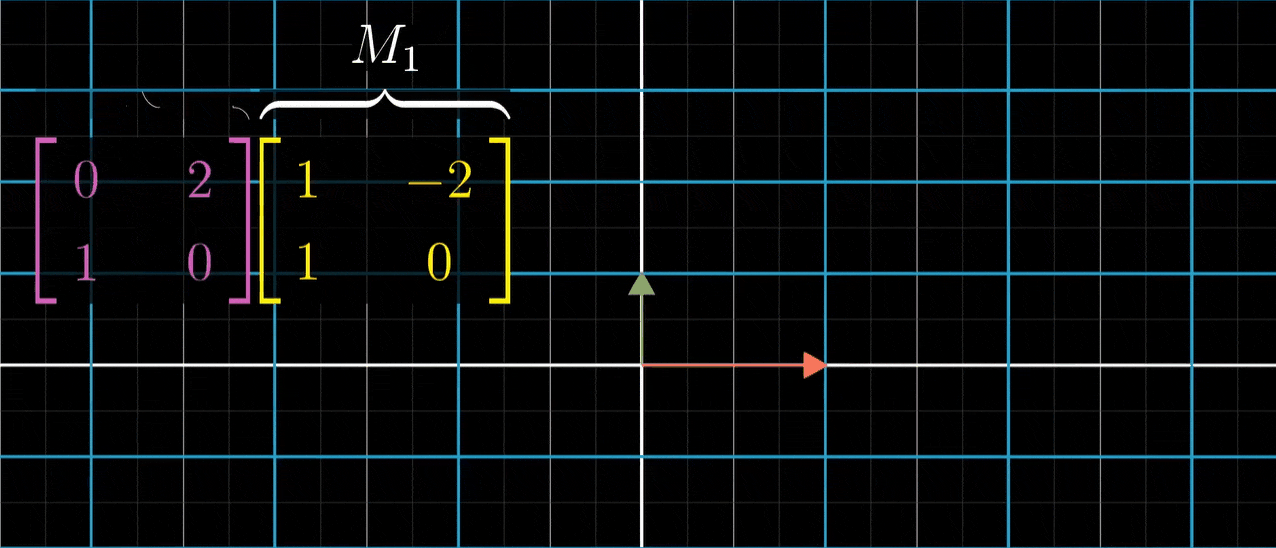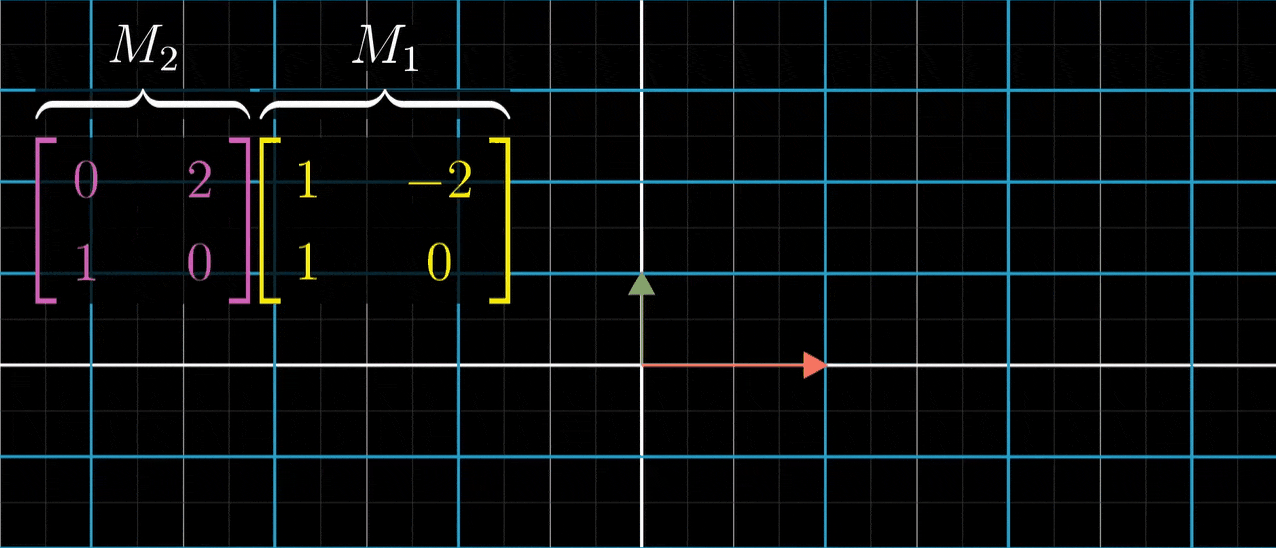
• M1和M2先后作用，总体效果是一个新的变换，我们来求解它的矩阵。但是这一次，我们来尝试一下不通过观看动画，只使用每个矩阵的数值来求解

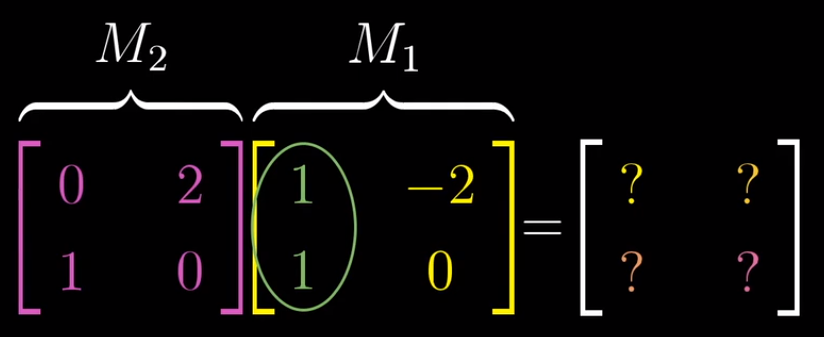
• 首先，我们得算出i帽的去向。在M1作用之后，按照定义，i帽的新坐标由M1的第一列给出，也就是（1，1）；要看看M2作用之后会发生什么，将矩阵M2乘以向量（1，1）；根据矩阵向量乘法计算得到向量（2，1），这就是复合矩阵的第一列

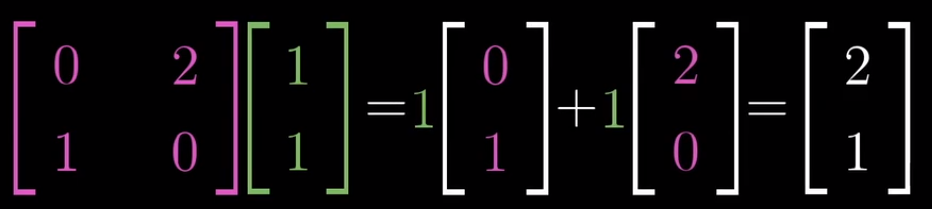
• 类似地，M1的第二列告诉我们j帽首先落在（-2，0），然后将M2作用于这个向量，根据矩阵向量乘法计算得到（0，-2），这就是复合矩阵的第二列

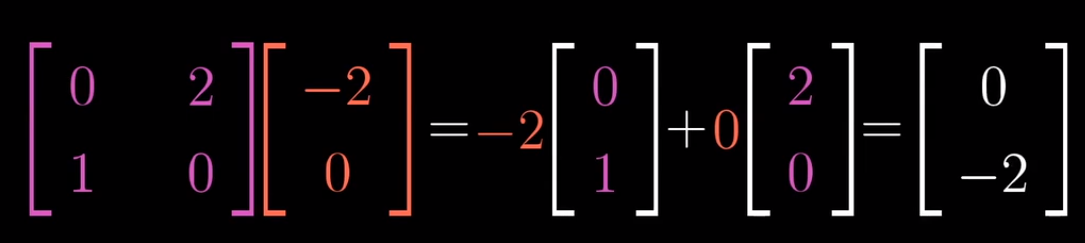
• 再重复一次同样的过程，不过这次我们用变量代替数值，只是为了说明这一推理过程对于任意矩阵都适用
• 要跟踪i帽的去向，首先找右侧矩阵的第一列，因为这是i帽首先到达的地方，将这一列左乘左侧的矩阵，结果就是i帽在第二个变换作用后的结果，所以复合矩阵的第一列，就是左侧矩阵与右侧矩阵第一列的乘积；类似地，j帽首先落在右侧矩阵第二列所代表的位置上，左侧矩阵与这一列相乘就能得到j帽的最终位置，因此这一乘积就是复合矩阵的第二列

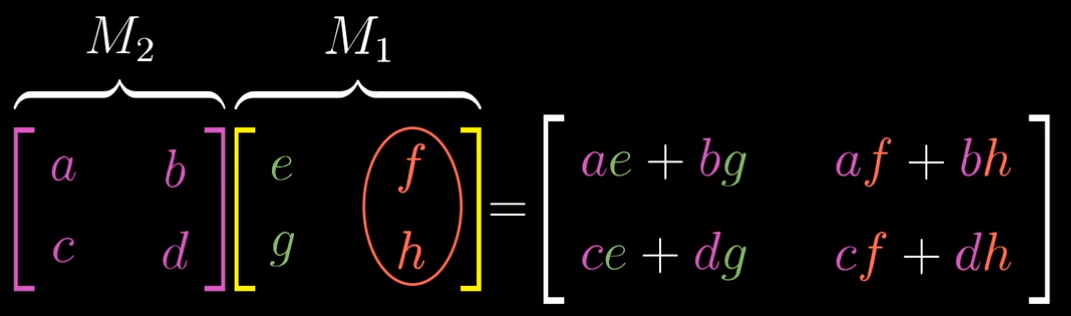
注意，应该养成思考矩阵乘法意义的习惯，也就是两个变换相继作用

• 比如说下面这个问题，矩阵相乘时，它们的先后顺序影响结果吗？

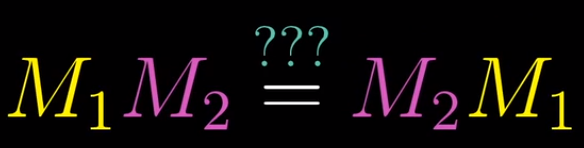
• 用一个简单的例子，比如之前提到的，一个是剪切，它保持i帽不变，将j帽挤到右边；另一个是90度旋转

• 如果你首先剪切，然后旋转，你会发现i帽落在（0，1），j帽落在（-1，1），它们彼此靠的很近

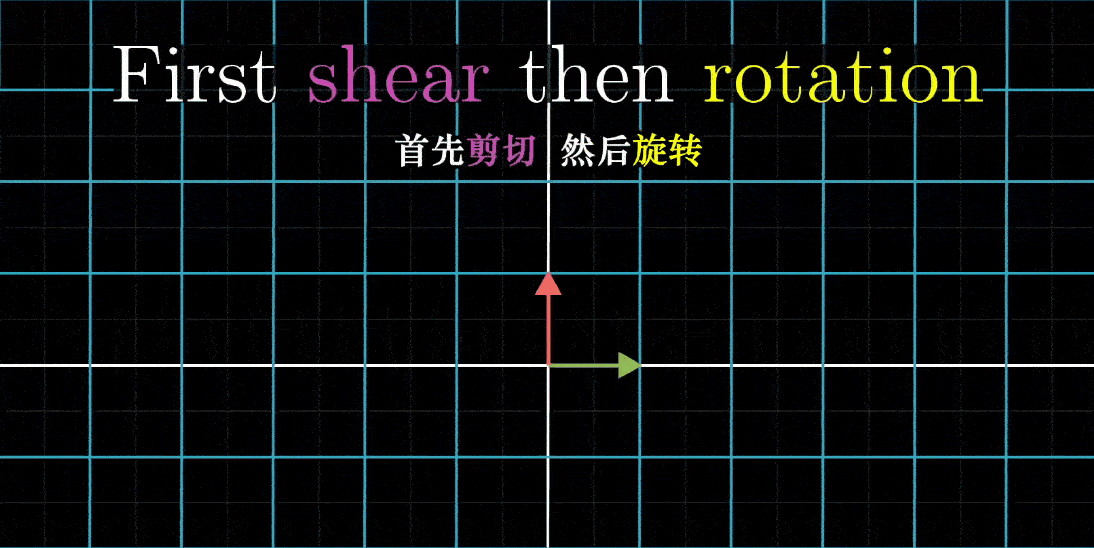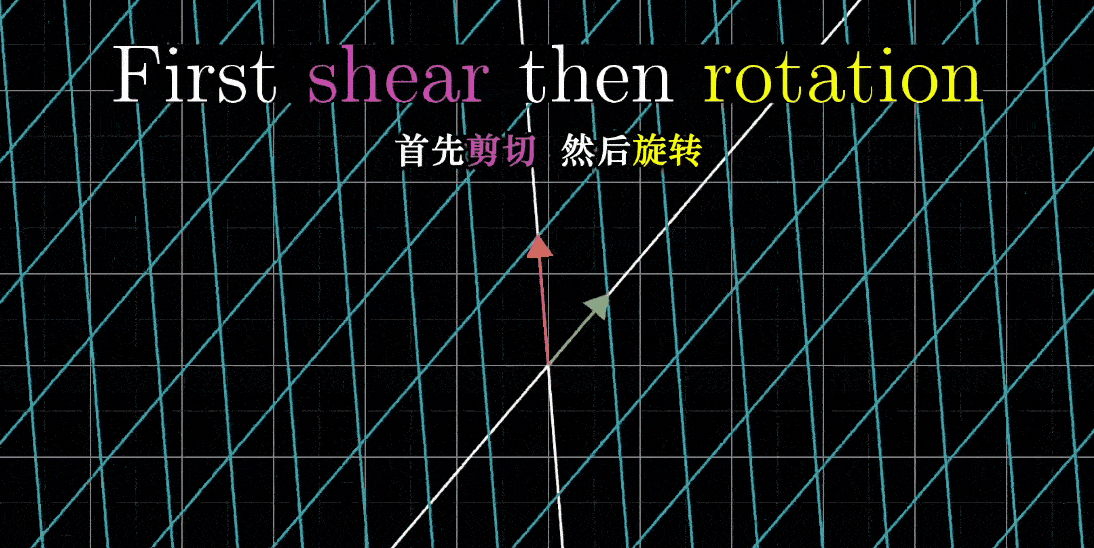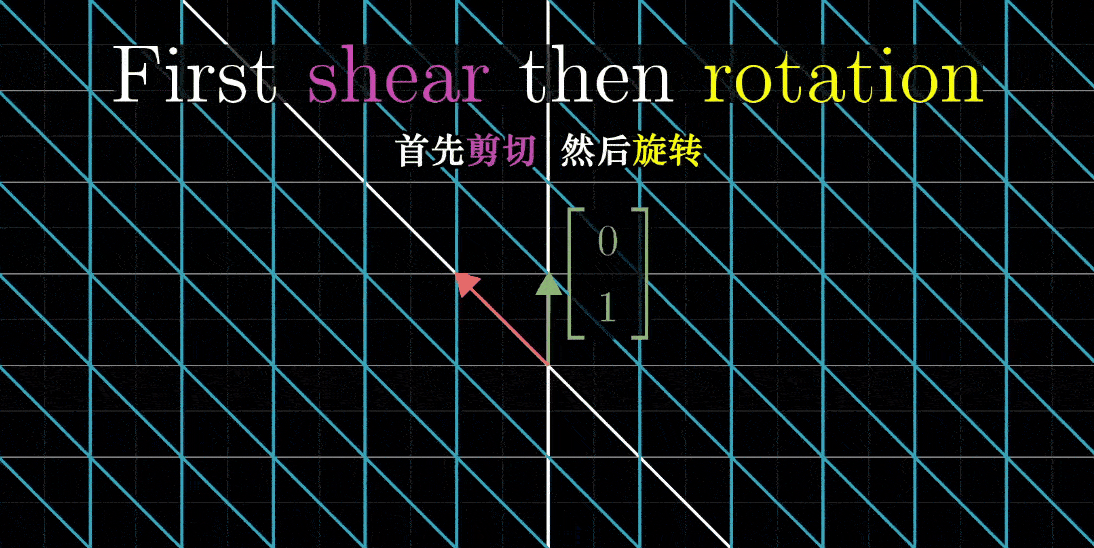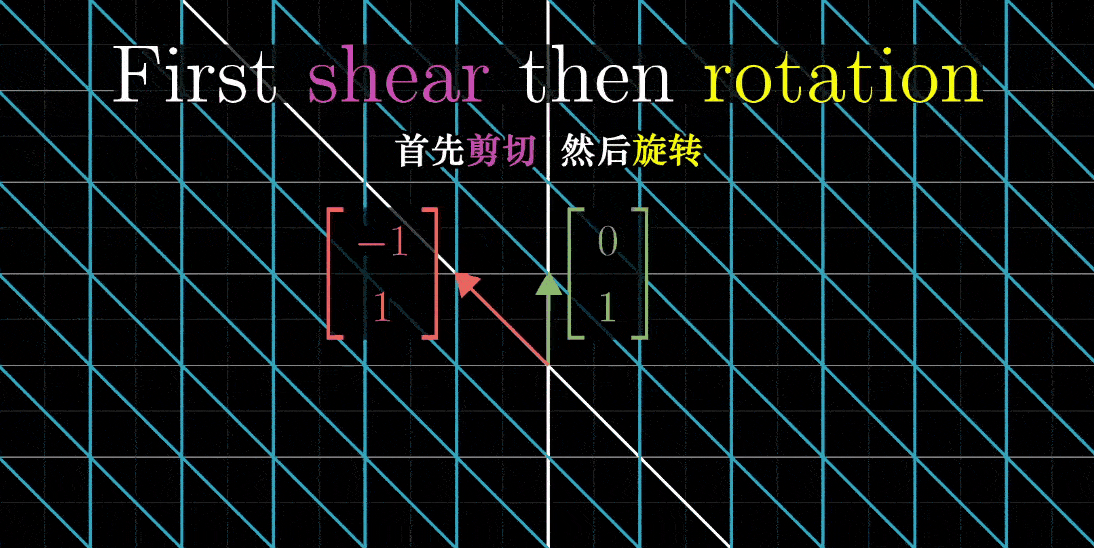
• 如果你首先旋转，然后剪切，i帽落在（1，1），而j帽落在一个不同的地方（-1，0），它们的指向分隔很远

• 二者的总体效应明显不同，所以乘积顺序显然会有影响

注意，我们在用变换来思考，这一过程可以在脑中形象地进行，完全不需要做矩阵乘法

结合律

• 矩阵乘法具有结合性
• 这是在说，如果你有三个矩阵A B C，然后将它们相乘，无论是首先计算A乘以B，然后将结果乘以C，还是先算B乘以C，然后将结果左乘A，二者的结果应该相同；换句话说，添不添加括号与结果无关

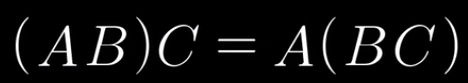
• 用变换相继作用的思想去考虑矩阵乘积
• 这是在说，首先应用C变换与B变换，然后应用A变换，与先应用C变换，然后应用B变换和A变换的结果相同，完全没有需要证明的东西，只是将同样的三个变换用同样的顺序依次作用而已