03-矩阵与线性变换
很遗憾,Matrix(矩阵)是什么是说不清的。你必须得自己亲眼看看。
—墨菲斯
线性变换
-
“变换” 本质上是 “函数” 的一种花哨的说法,它接收输入内容,并输出对应结果。特别地,在线性代数的情况下,我们考虑的是接收一个向量并且输出一个向量的变换
-
既然 “变换” 和 “函数“ 意义相同,为什么还要使用前者而不是后者?因为使用“变换”是在暗示以特定方式来可视化这一输入-输出关系
-
一种理解 “向量的函数” 的方法是使用运动。如果一个变换接收一个向量并输出一个向量,我们想象这个输入向量移动到输出向量的位置

- 接下来,要理解整个变换,我们可以想象每一个输入向量都移动到对应输出向量的位置
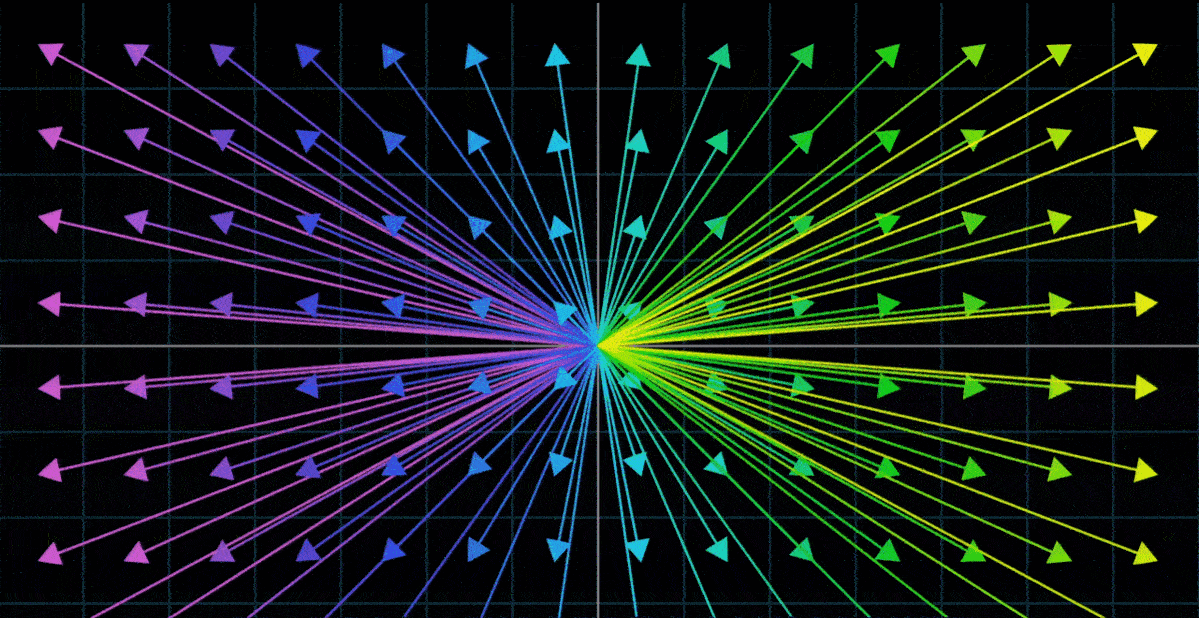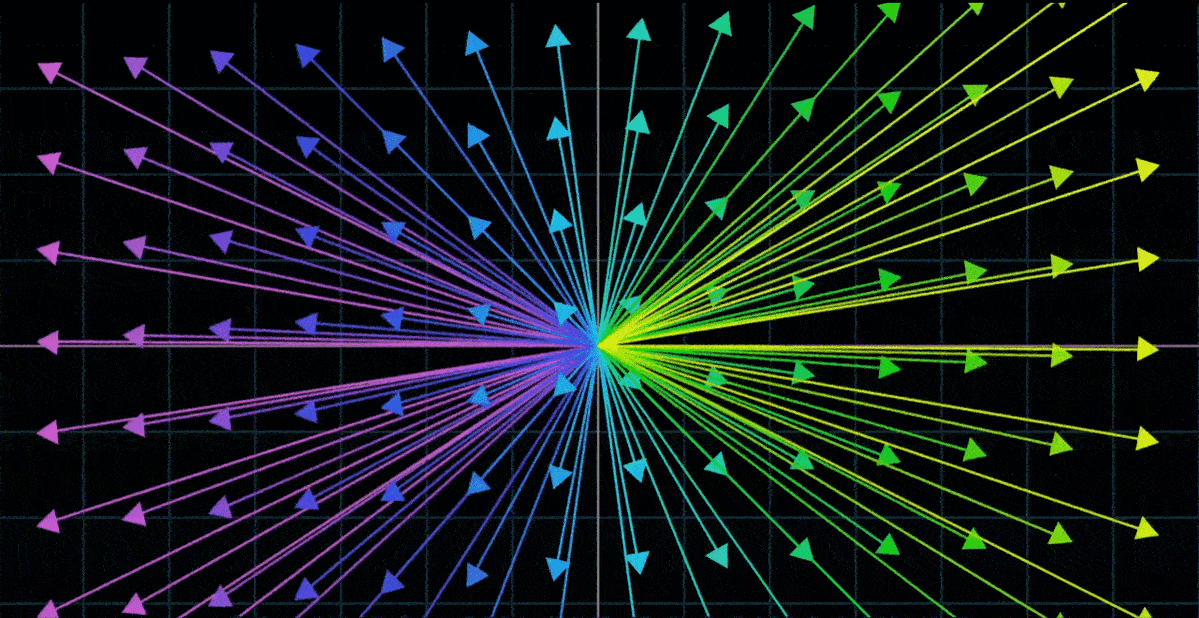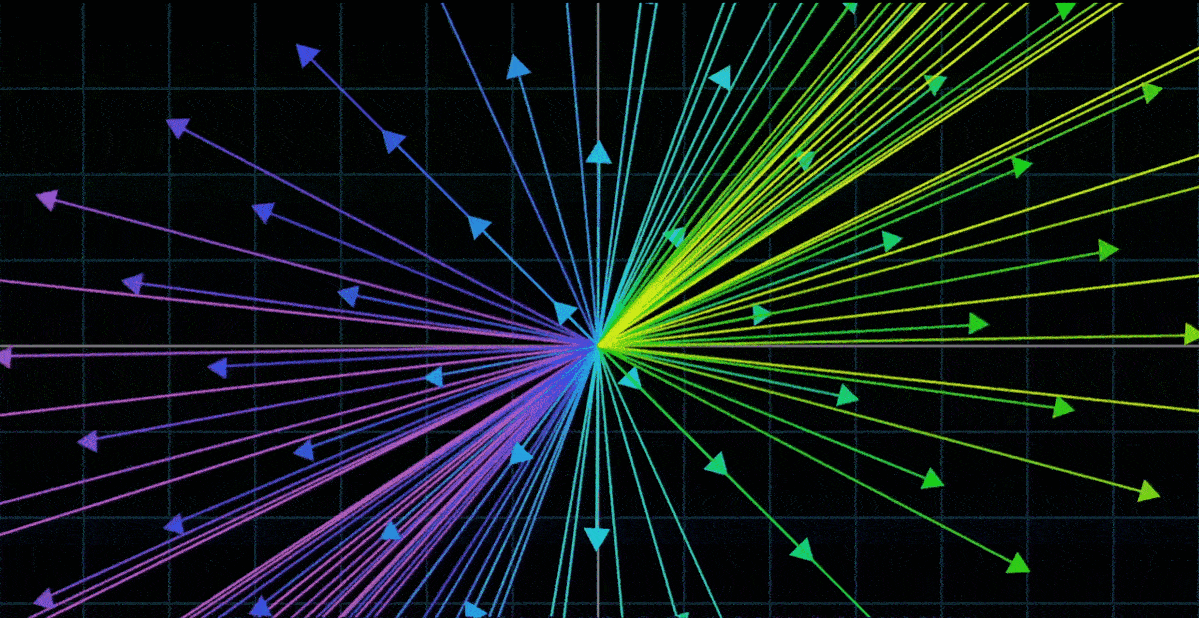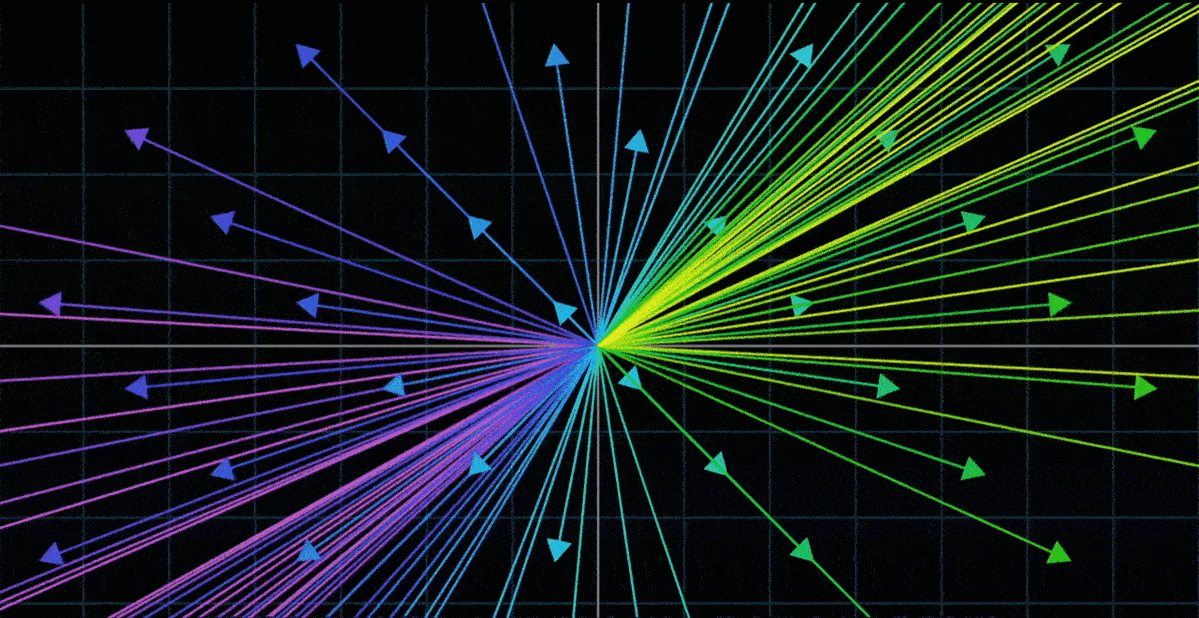
- 因为将向量看作箭头时,同时考虑所有二维向量会变得非常拥挤,所以将每一个向量看作它的终点,而不是一个箭头。用这种方法考虑所有输入向量都移动到对应输出向量的位置时,我们只用看空间中的所有点移动到其他点的位置
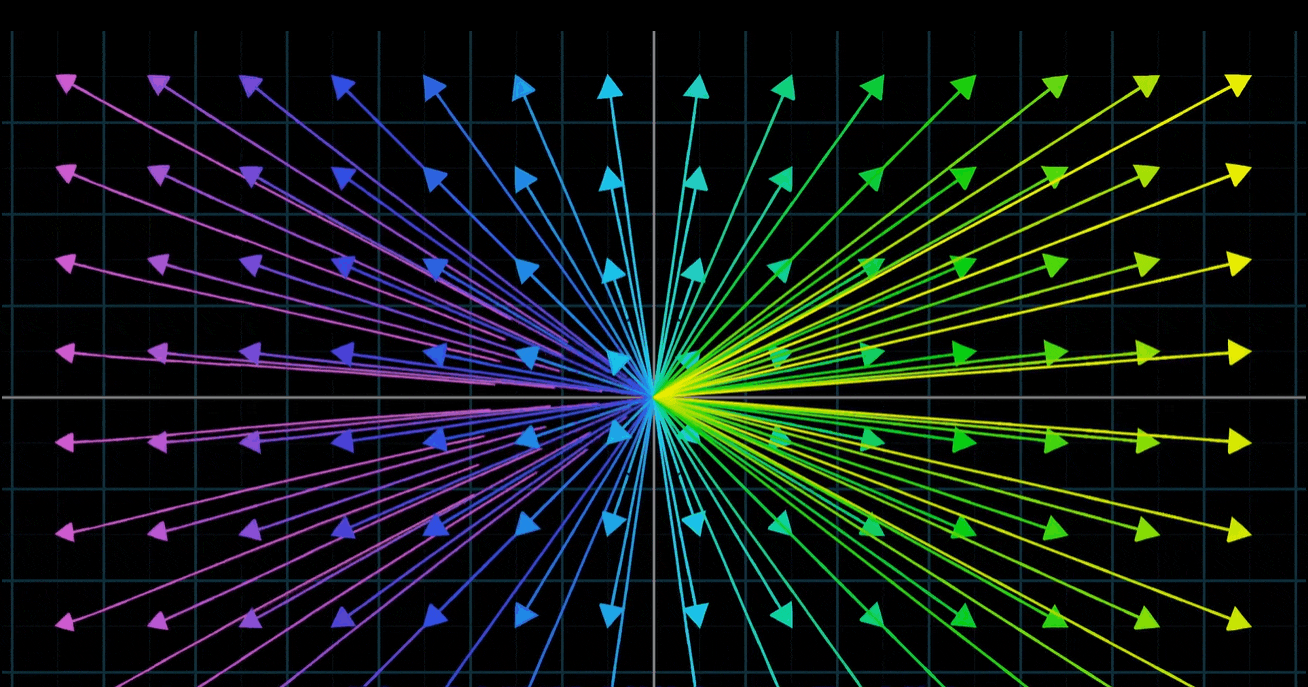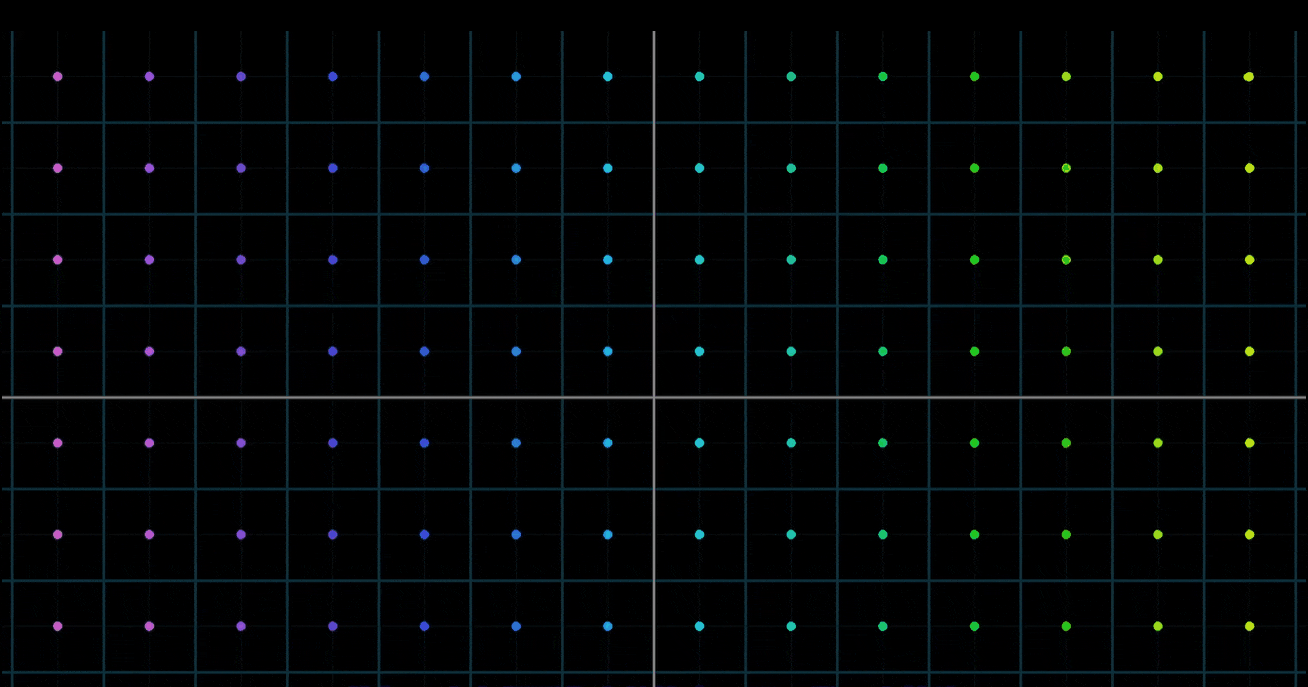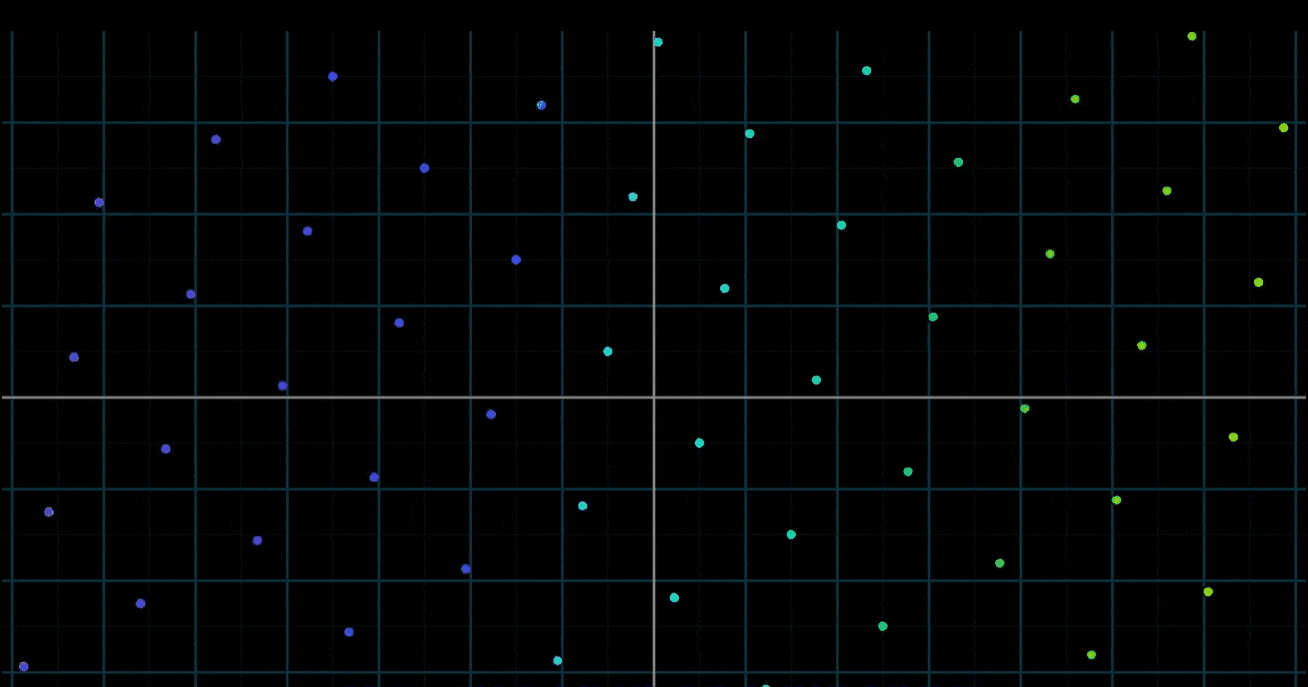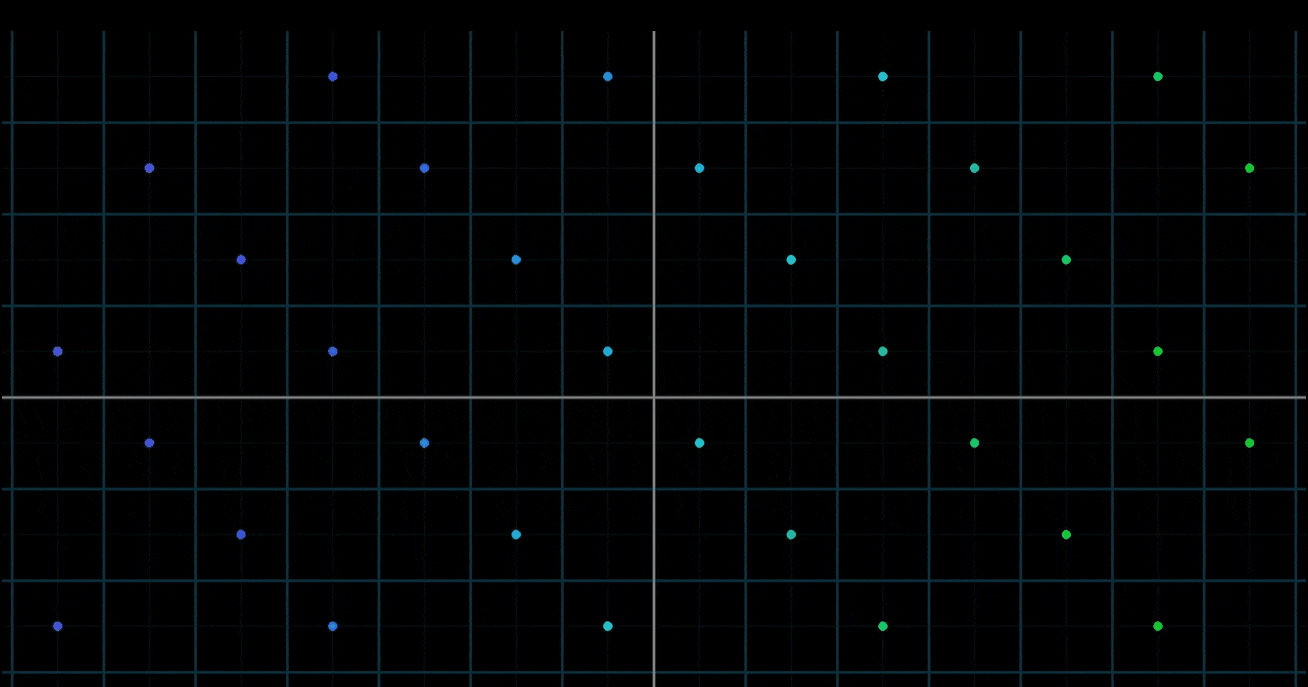
- 二维空间变换这种情况下,为了更好地体会整个空间形状上的改变,可以对无限网络上的所有点同时做变换;也可以在背景中保留原始网格的副本,以便追踪终点与起点的相对关系
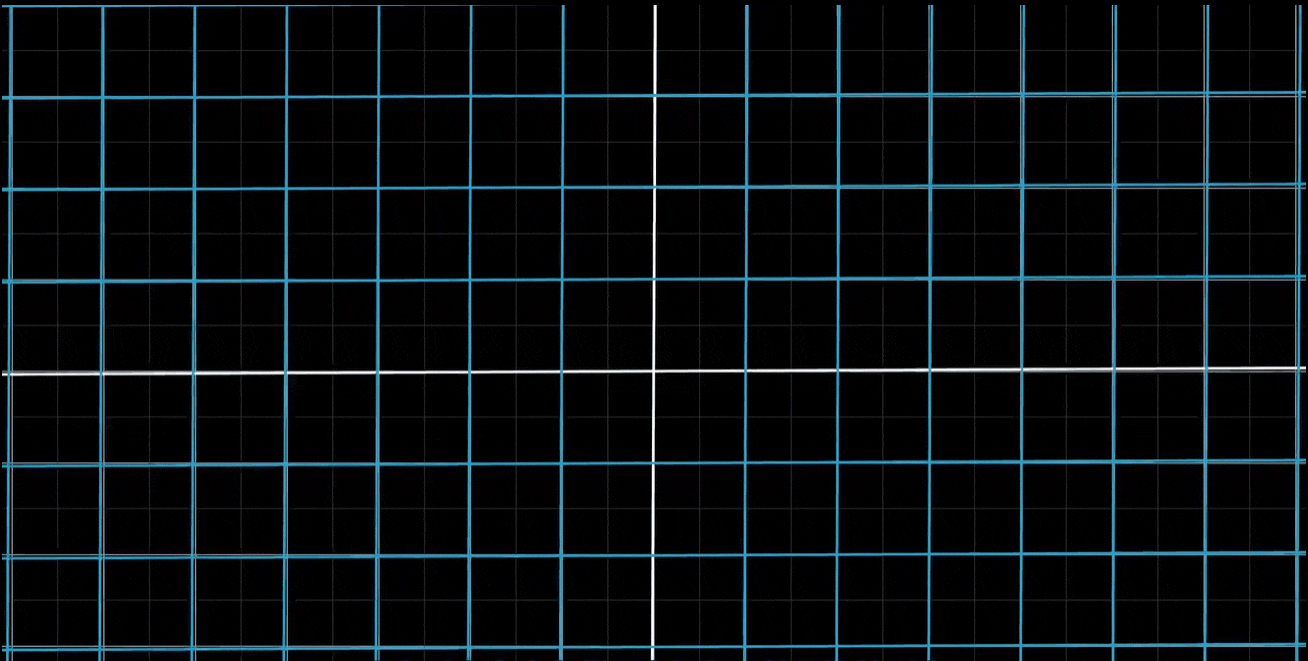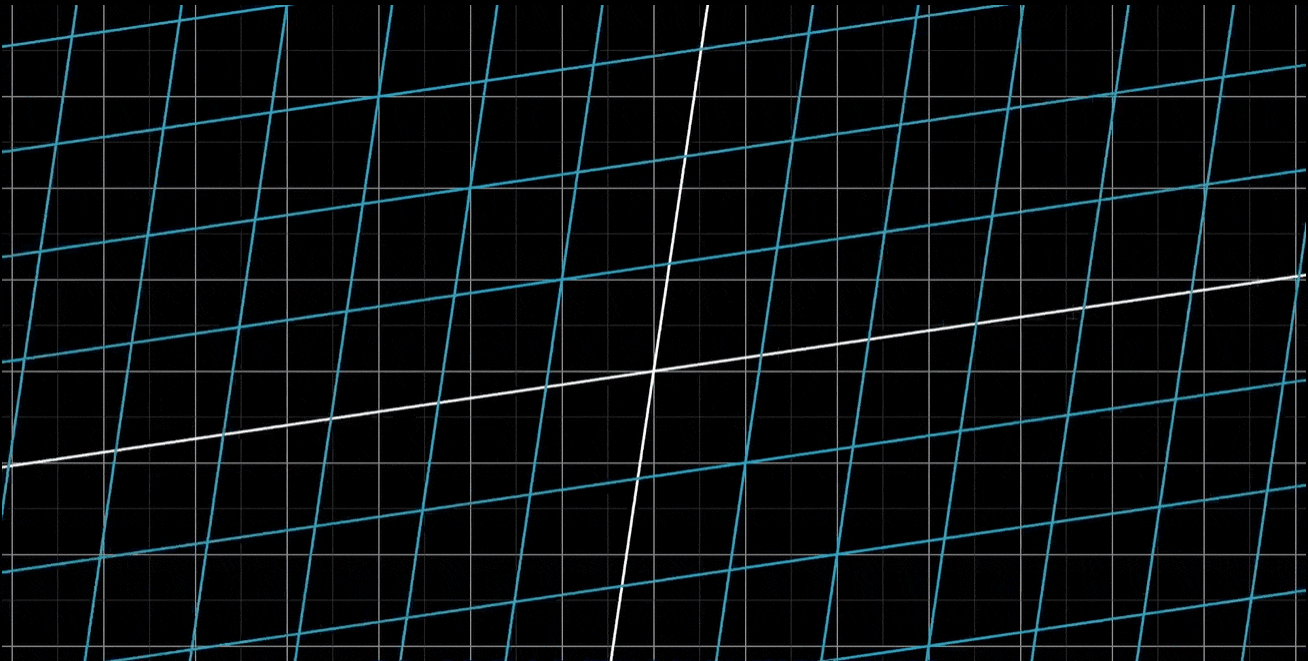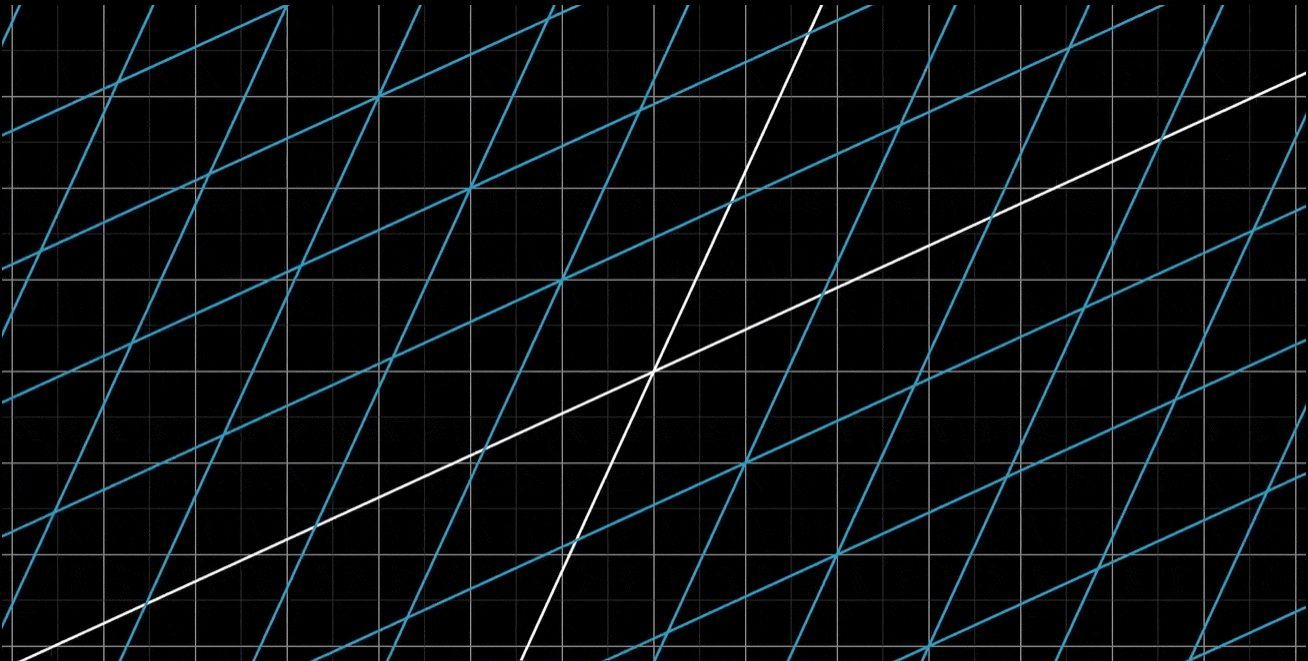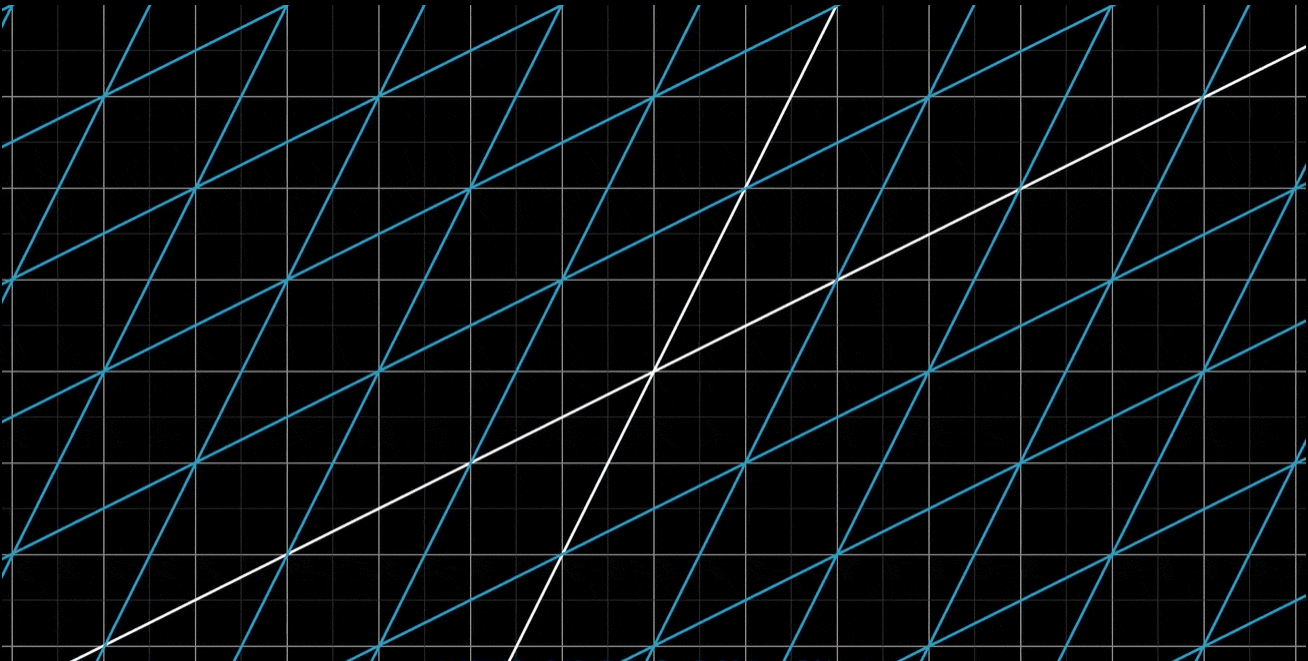
-
任意一个对空间的变换可以非常复杂,但幸运的是,线性代数限制在一种特殊类型的变换上,这种变换更容易理解,称为“线性变换”
-
直观地说,如果一个变换具有以下两条性质,我们就称它是线性的
-
一是直线在变换后仍然保持为直线,不能有所弯曲
-
二是原点必须保持固定
-
-
总的来说,应该把线性变换看作是 “保持网格线平行且等距分布” 的变换
矩阵
- 如何用数值描述线性变换?应该给计算机什么样的计算公式,使得你给它一个向量的坐标,它能给你变换后向量的坐标呢?

- 实际结果是,只需要记录两个基向量i帽和j帽变换后的位置,其他向量都会随之而动
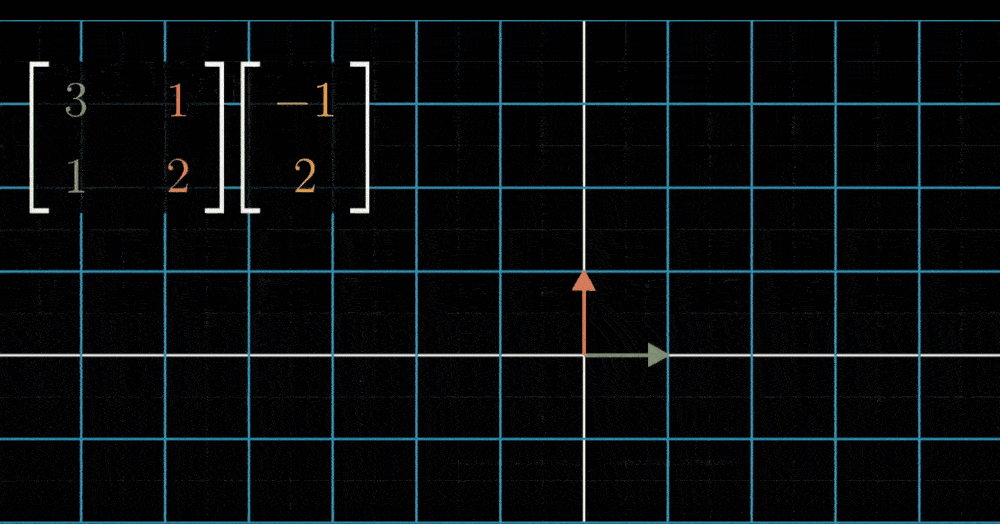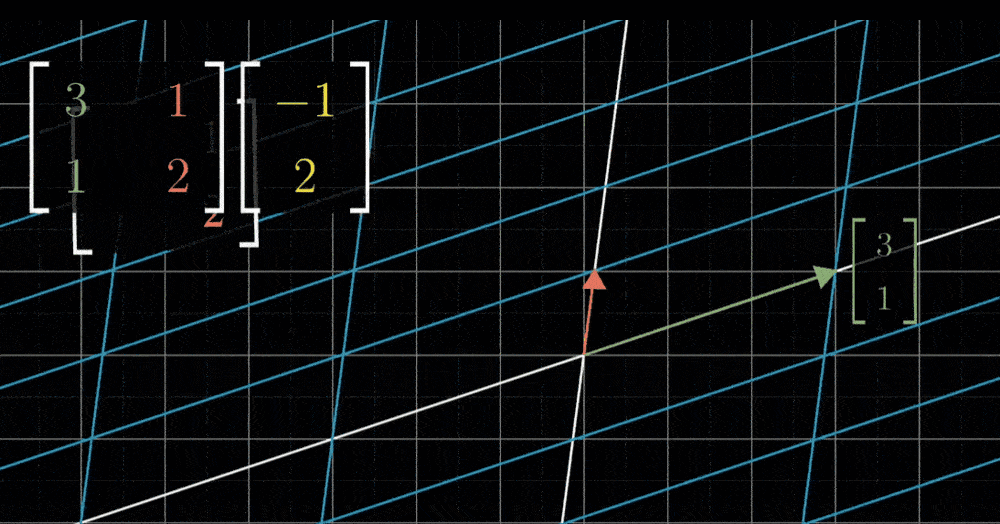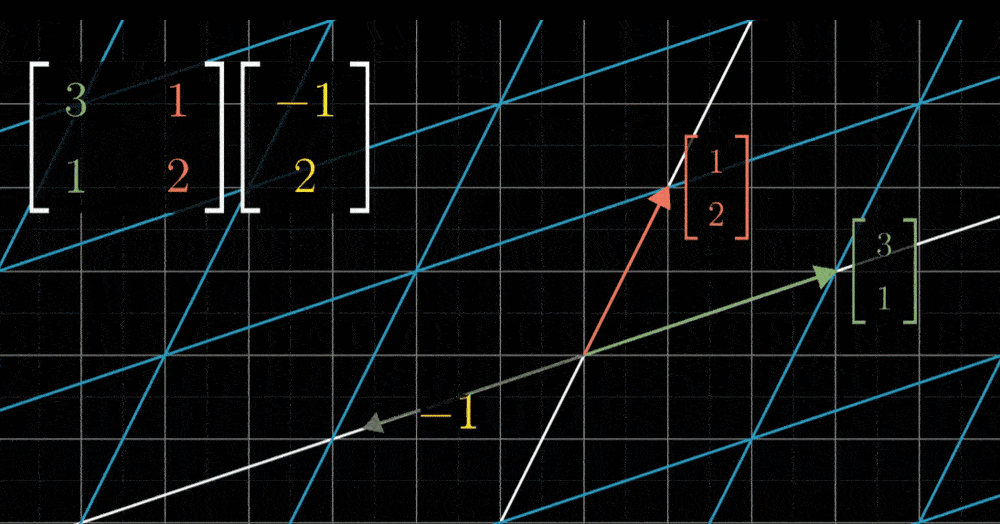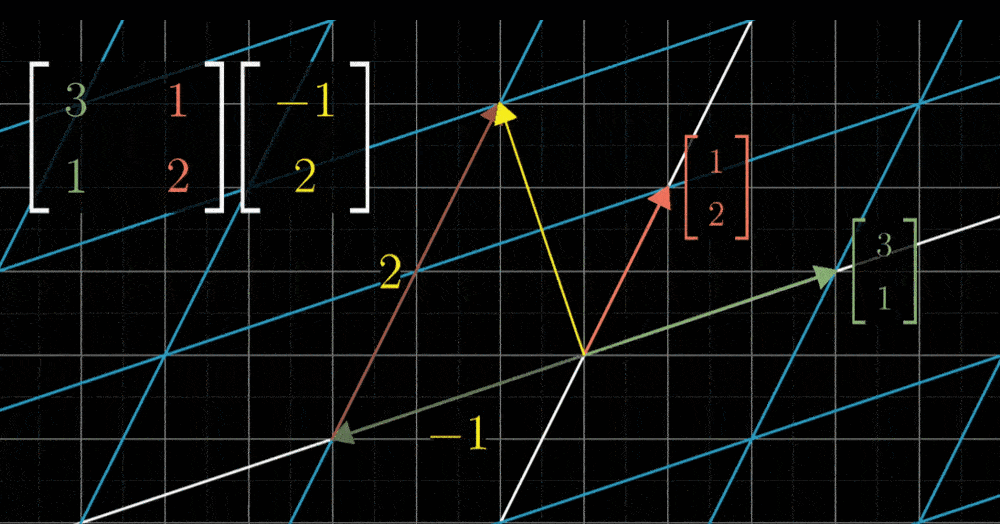
- 例如,考虑坐标为(-1,2)的向量v,这个向量就是-1与i帽之积和2与j帽之积的和
-
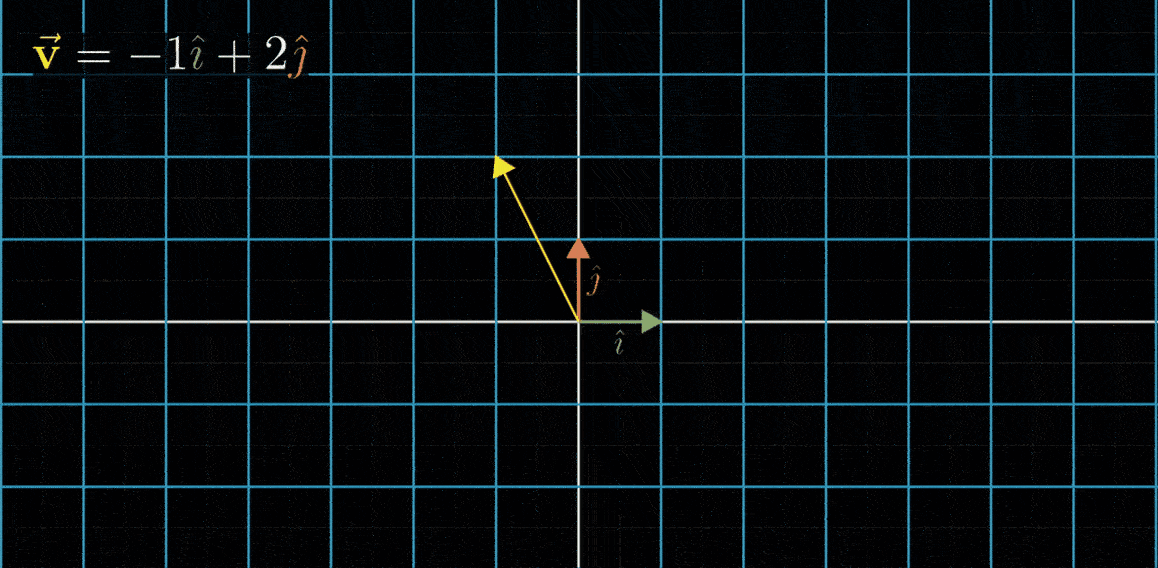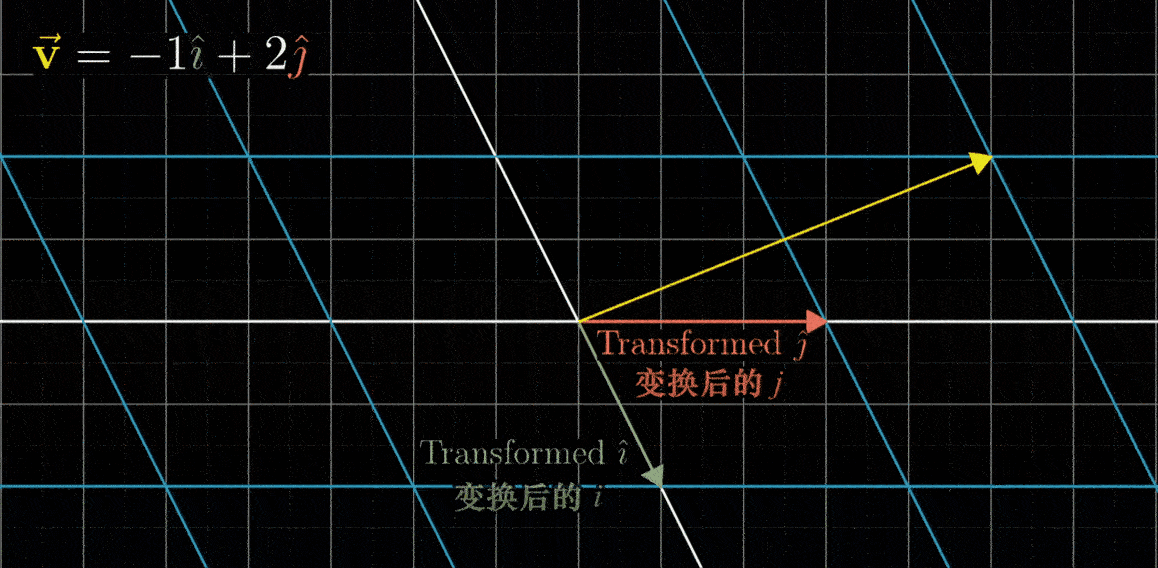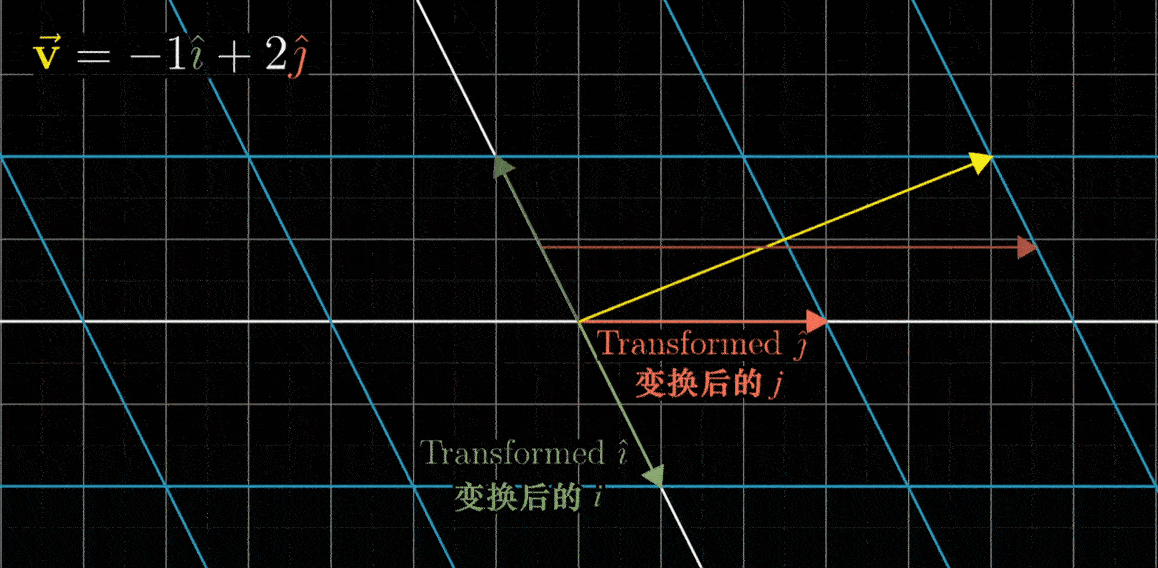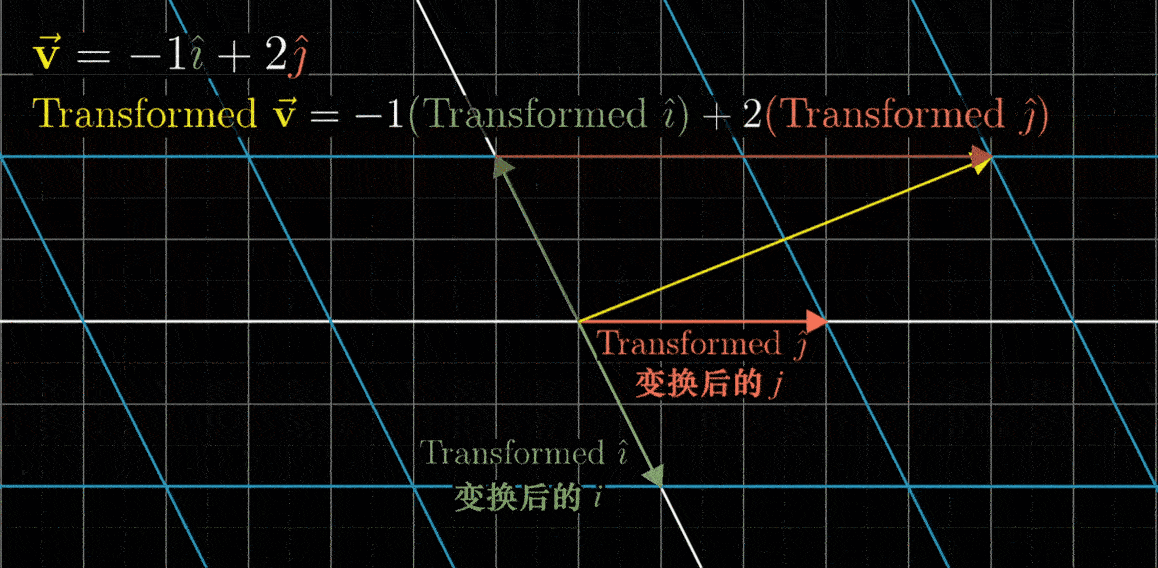
网格线保持平行且等距分布的性质有一个重要的推论:变换后的向量v的位置,是-1与变换后的i帽之积,加上2与变换后的j帽之积。换句话说,如果向量v是i帽和j帽的一个特定线性组合,那么变换后的向量v也是变换后i帽和j帽的同样的线性组合。这意味着,可以只根据变换后的i帽和j帽,就推断出变换后的v。这也是在背景中保留原始网格的副本的原因
-
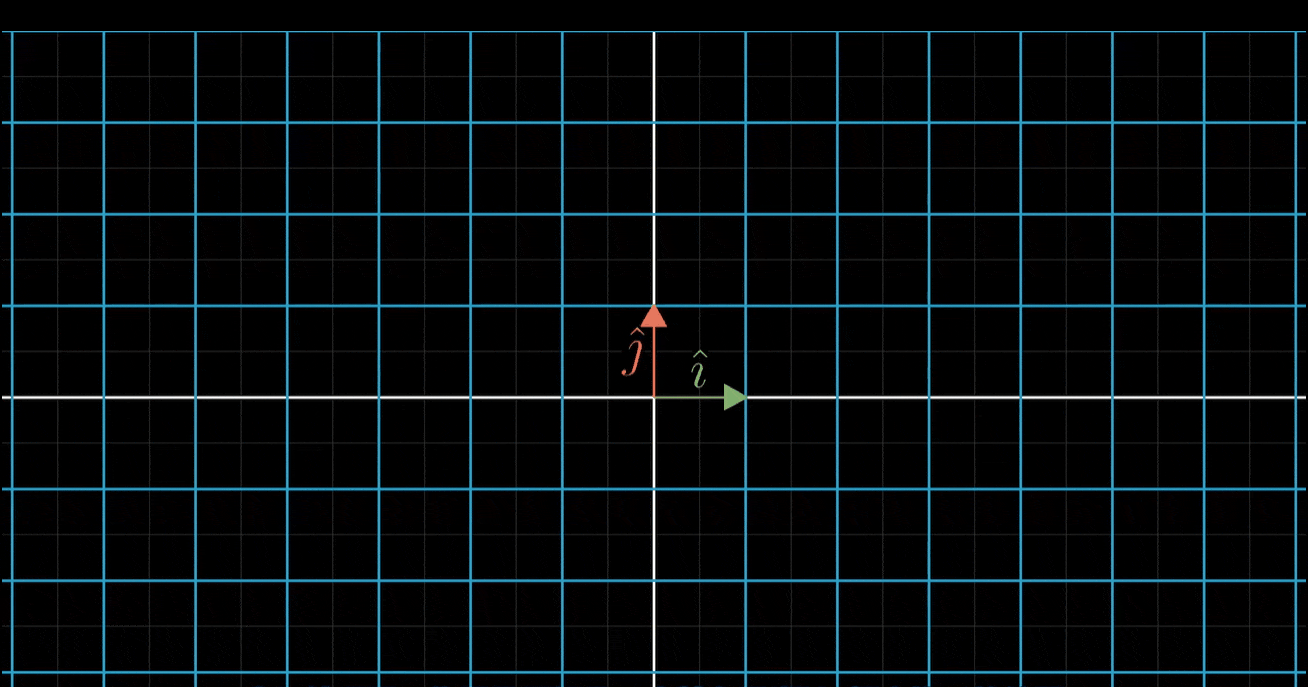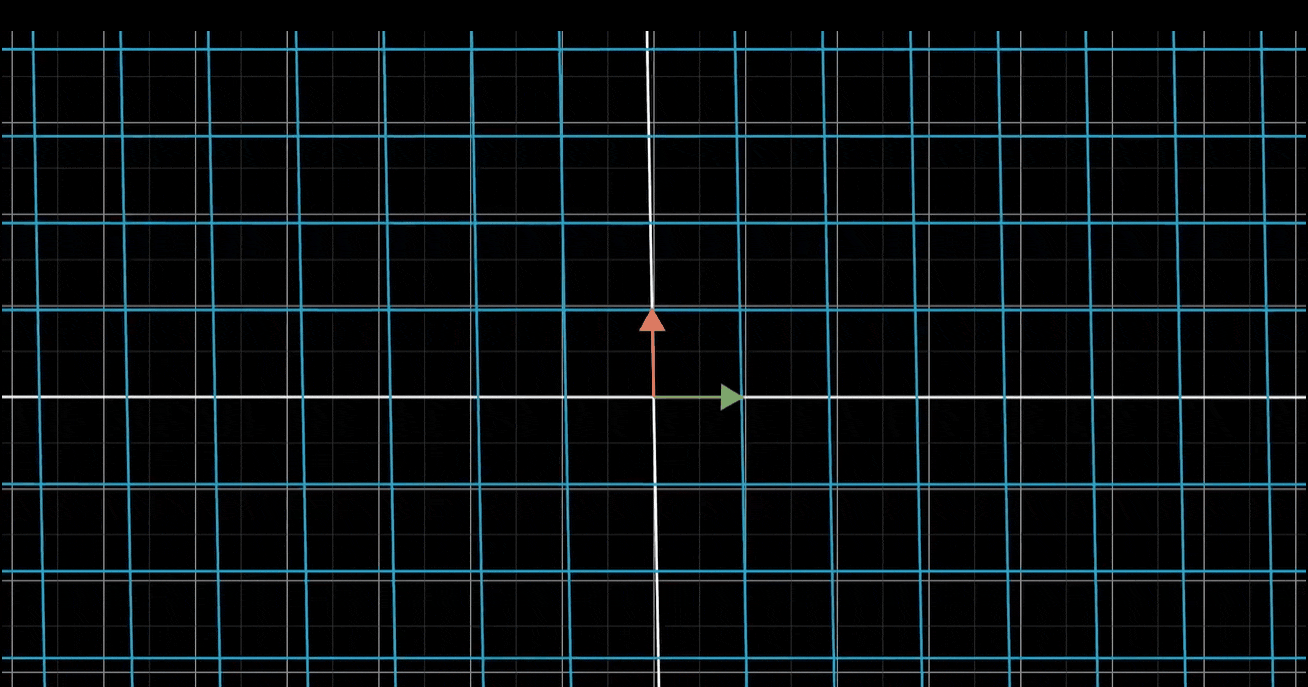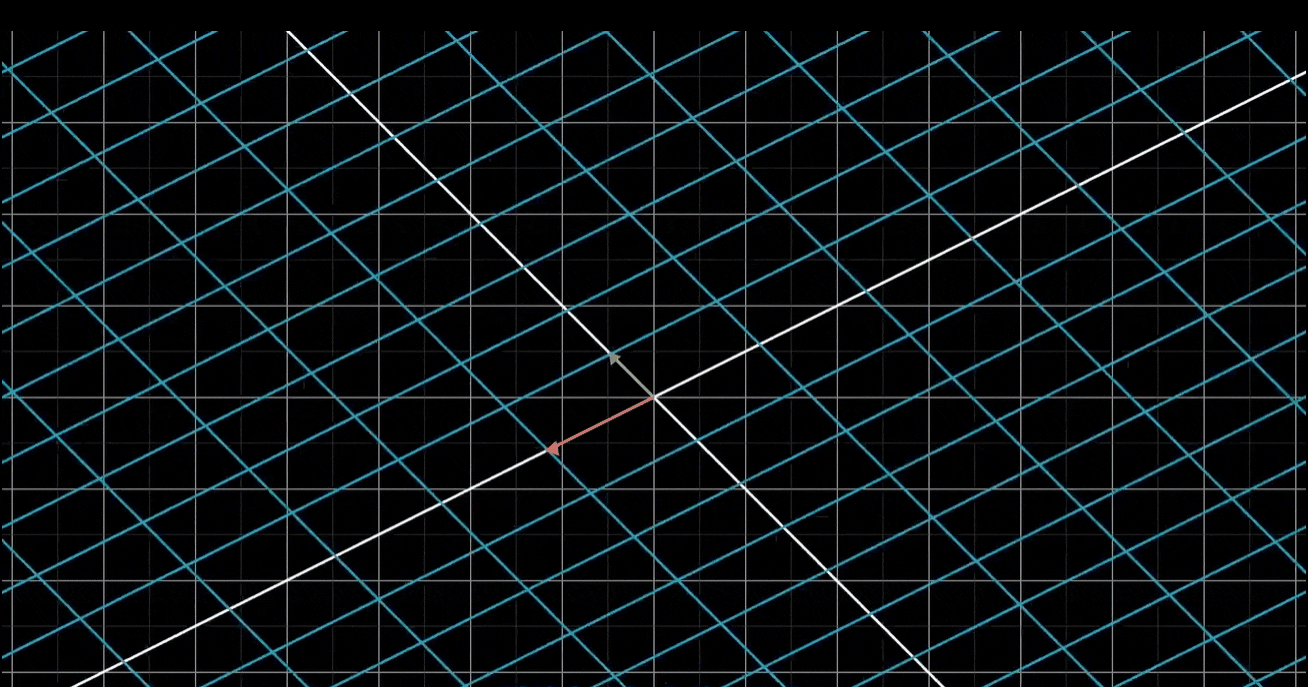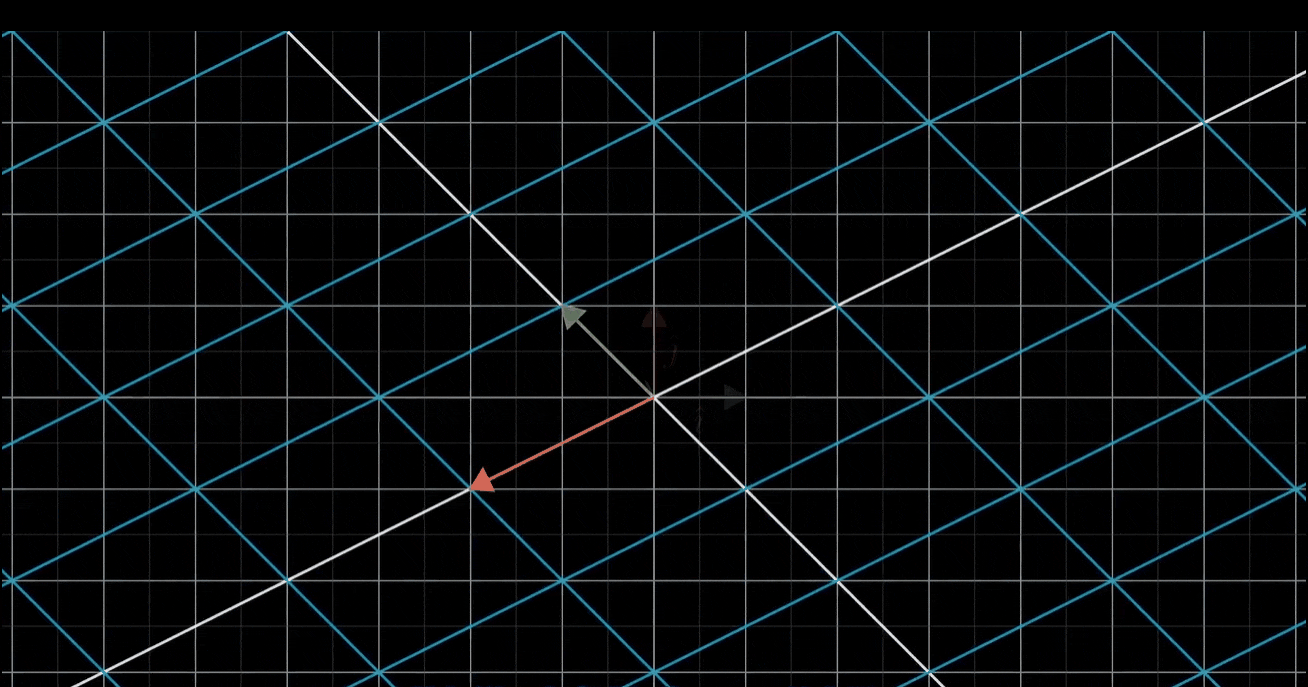
对于现在所示的变换,我们可以看出i帽落在坐标(1,-2)上,j帽落在x轴上,坐标为(3,0),也就是说,-1乘以i帽加上2乘以j帽所代表的向量,会落在-1乘以向量(1,-2)加上2乘以向量(3,0)的位置上,简单运算之后,就能推断出向量v一定落在向量(5,2)上

-
一般情况下,一个向量的坐标是(x,y),变换后的这个向量就是x乘以变换后的i帽(1,-2),加上y乘以变换后的j帽(3,0),简单运算之后你就可以知道它落在坐标(1x + 3y,-2x + 0y)上。运用这个公式,我给你任意一个向量,你都能告诉我它在变换后的位置
-
只要记录了变换后的i帽和j帽,我们就可以推断出任意向量在变换之后的位置,完全不必观察变换本身是什么样
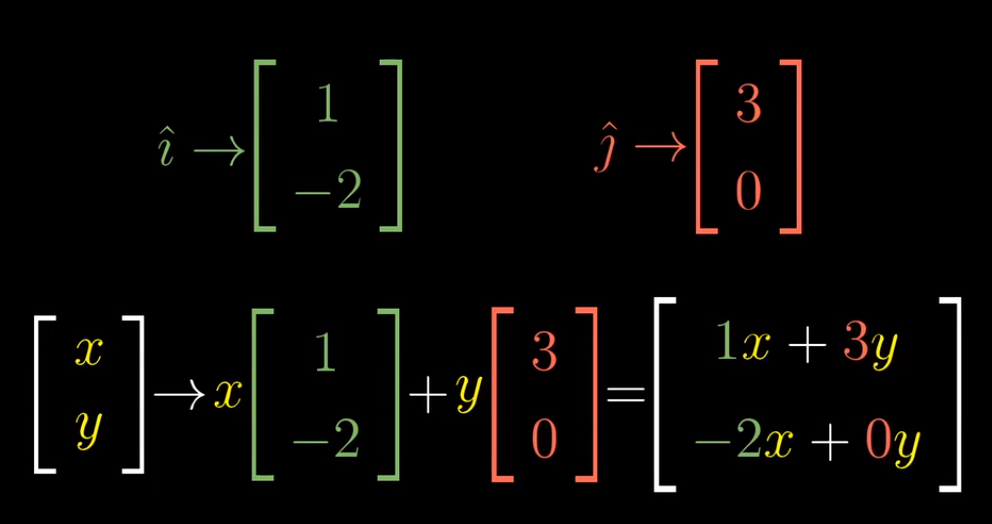
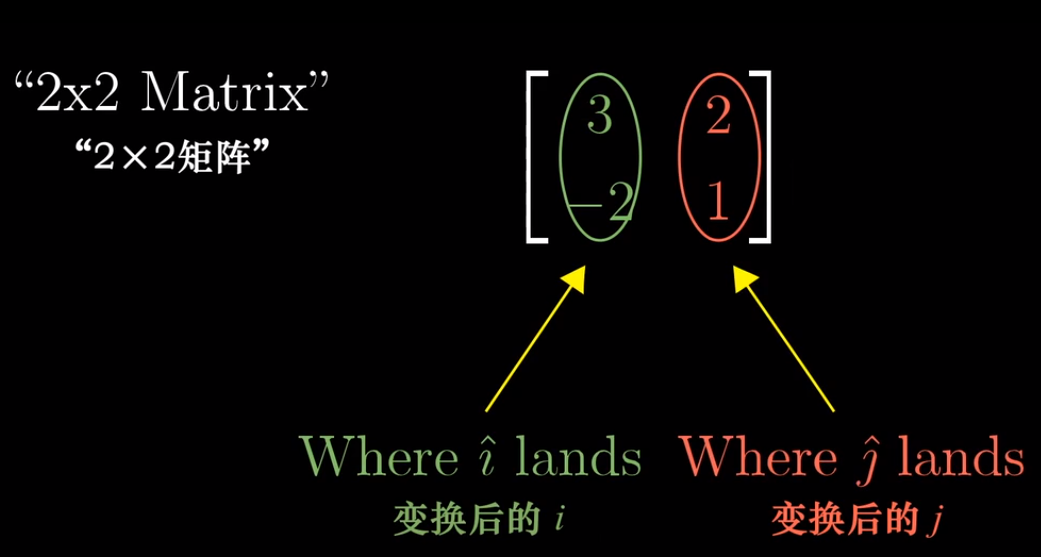
- 以上内容是在说,一个二维线性变换仅由四个数字完全确定,变换后i帽的两个坐标与变换后j帽的两个坐标。通常我们将这些坐标包装在一个2 x 2的格子中,称它为2 x 2矩阵。你可以把它的列理解为两个特殊的向量,即变换后的i帽和j帽
- 如果你有一个描述线性变换的2 x 2矩阵,以及一个给定向量,你想了解线性变换对这个向量的作用,你只需要取出向量的坐标,将它们分别与矩阵的特定列相乘,然后将结果相加即可,这与 “缩放基向量再相加” 的思想一致
- 更一般的情况下,我们来看看矩阵是[ [a,b],[c,d] ]时会发生什么。记住,矩阵在这里只是一个记号,它含有描述一个线性变换的信息,把第一列(a,c)看作是变换后的第一个基向量,把第二列(b,d)看作是变换后的第二个基向量,我们让这个变换作用于向量(x,y),结果是什么?那就应该是x乘以(a,c)加上y乘以(b,d),合并之后,得到向量(ax + by,cx + dy),你甚至可以把它定义为矩阵向量乘法,这里矩阵放在向量左边,类似一个函数
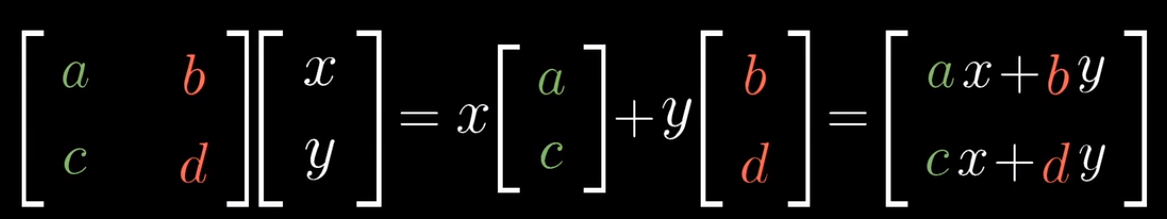
- 但是我们完全可以把矩阵的列看作变换后的基向量,把矩阵向量乘法看作它们的线性组合
拾遗
-
接下来练习用矩阵描述一些线性变换,比如说,将整个空间逆时针旋转90度,那么i帽落在坐标(0,1)上,j帽落在坐标(-1,0),那么这个矩阵的列就分别是(0,1)和(-1,0),如果想算出任意向量在逆时针旋转90度后的位置,只需要把它与矩阵相乘即可
-
这里还有一个有趣的变换,它有个特殊的名称叫“剪切”,在这个变换里,i帽保持不变,所以矩阵第一列为(1,0),但是j帽移动到了坐标(1,1),所以矩阵第二列为(1,1),为了计算给出定向量在剪切变换后的位置,只需要将矩阵与这个向量相乘即可
-
反过来看看问题,从一个矩阵出发,比如说一个以(1,2)和(3,1)为列的矩阵,如何推测出它代表的线性变换是什么样的?这里给出一种方法:首先将i帽子移动到(1,2),然后将j帽移动到(3,1),空间其他剩余部分随二者一起移动,以保持网格线平行且等距分布
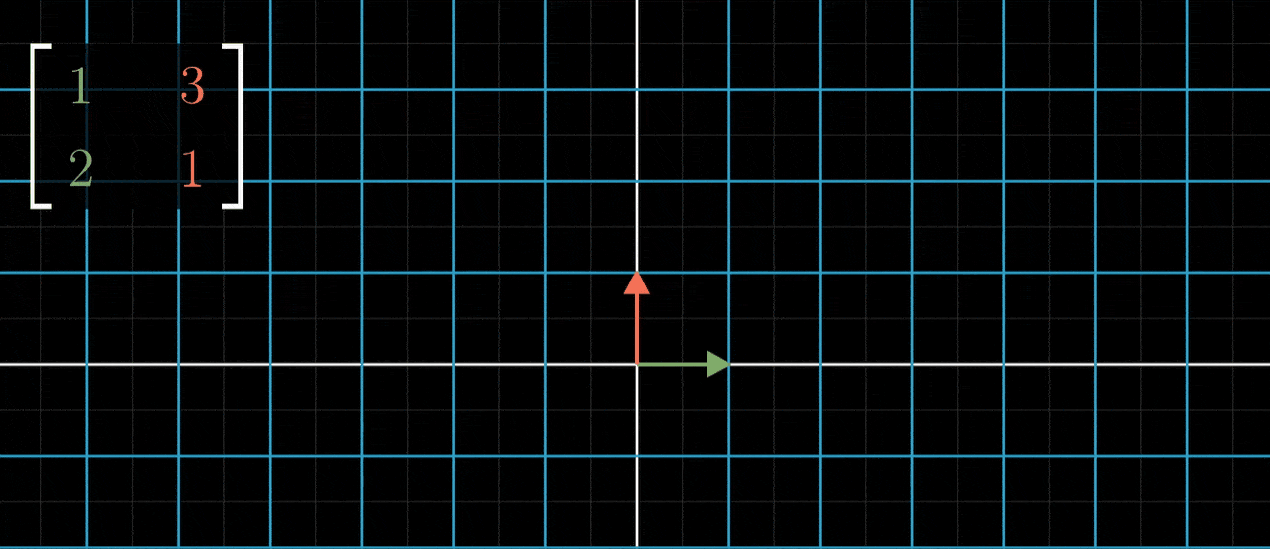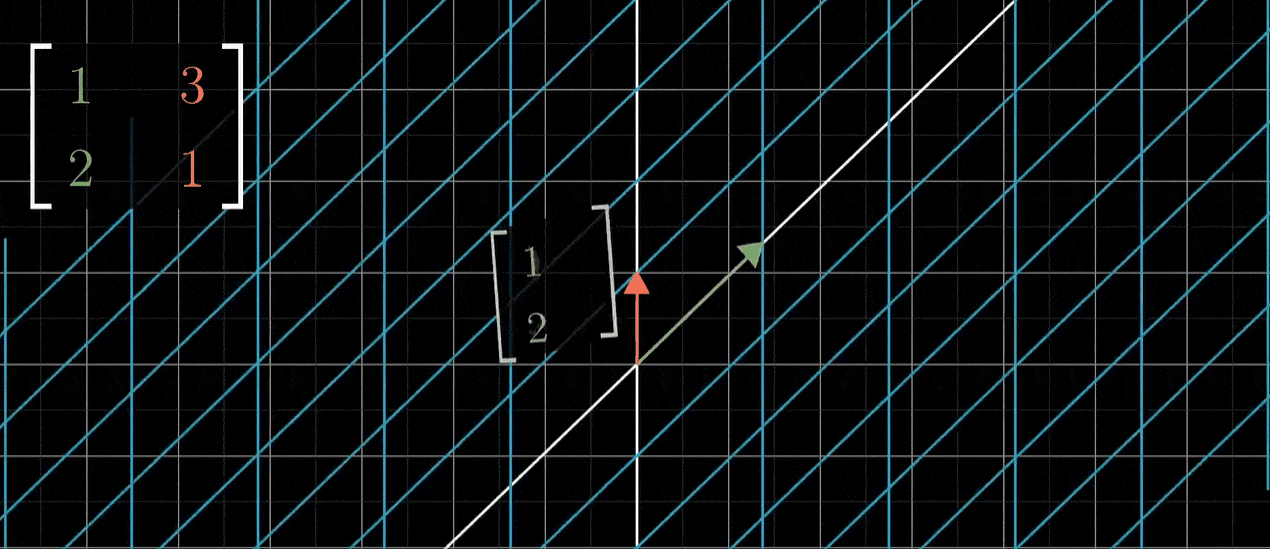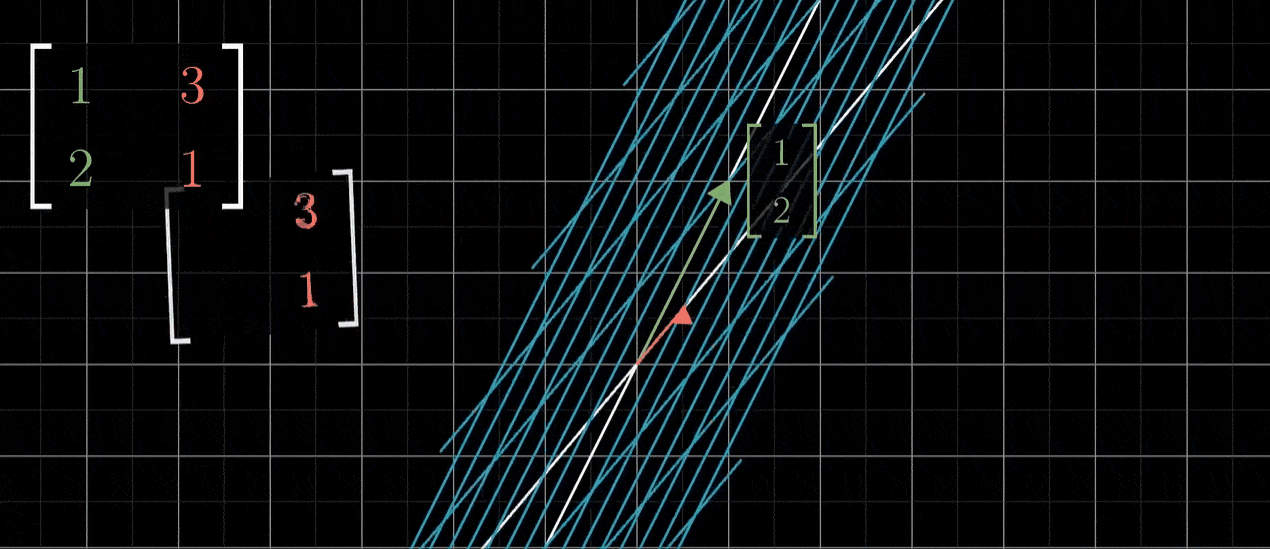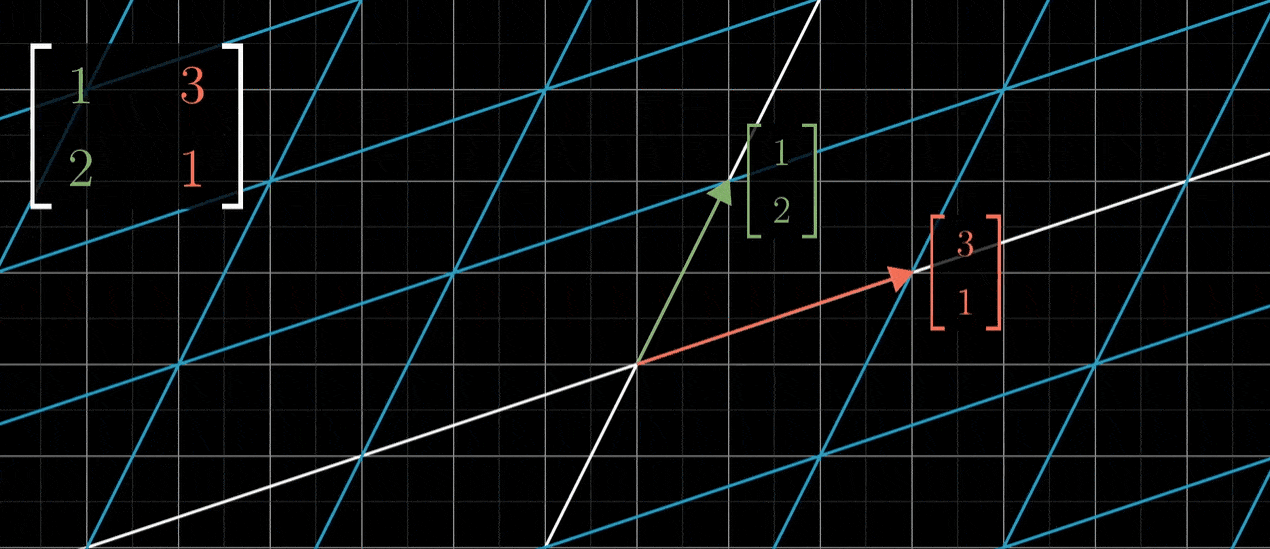
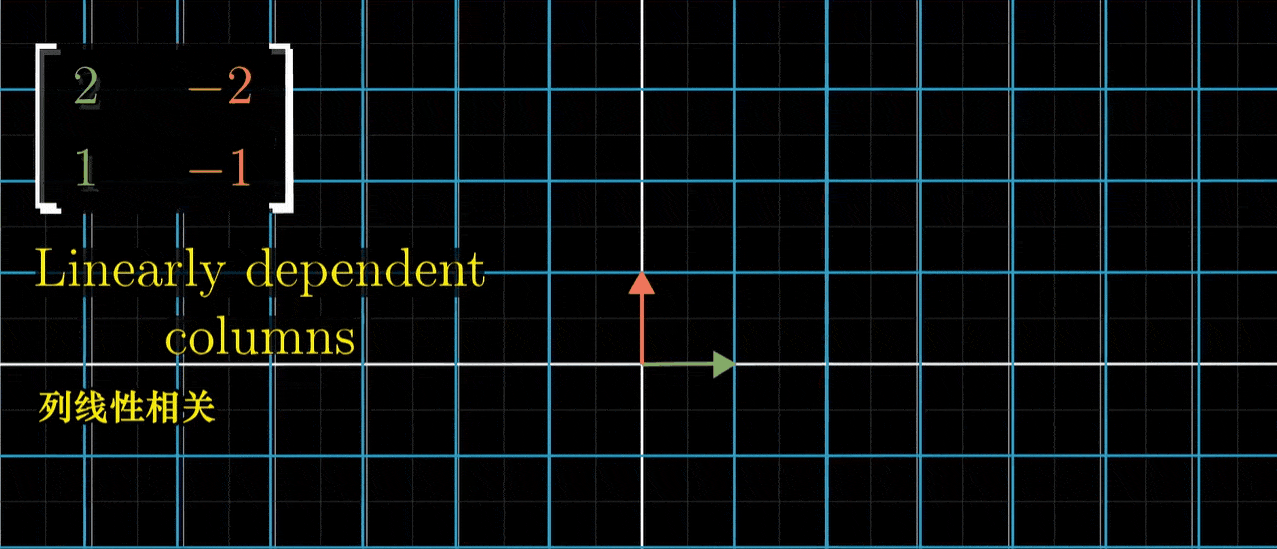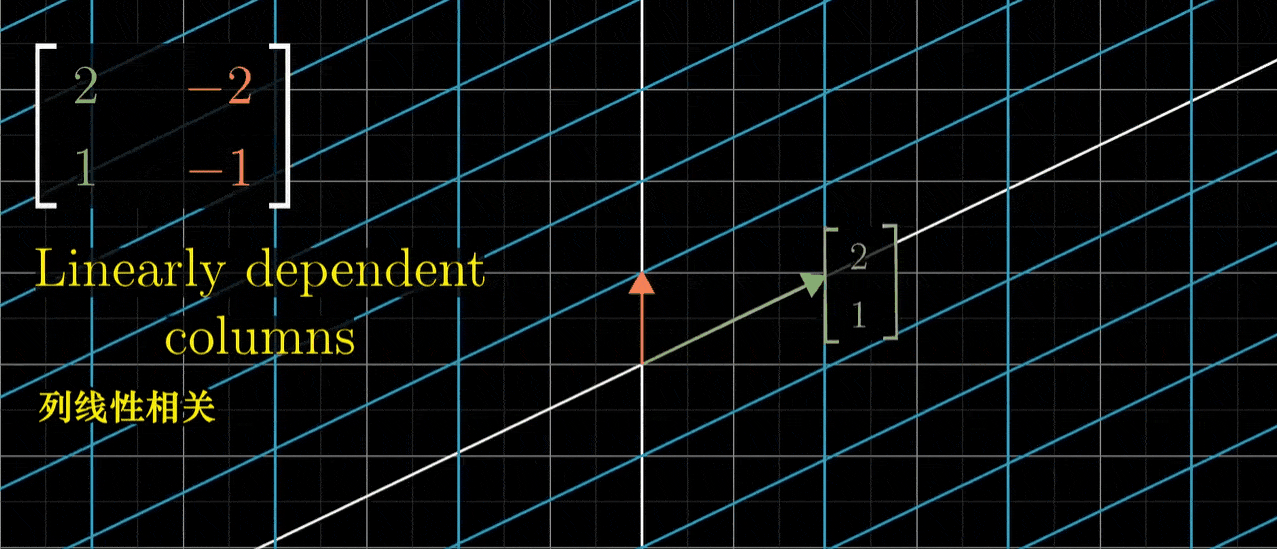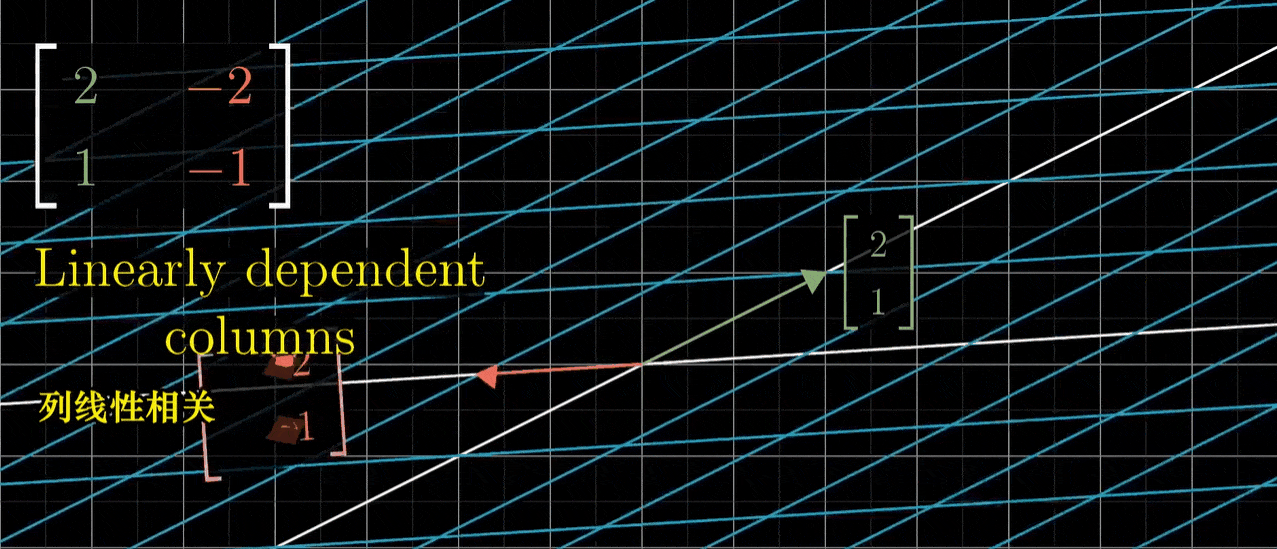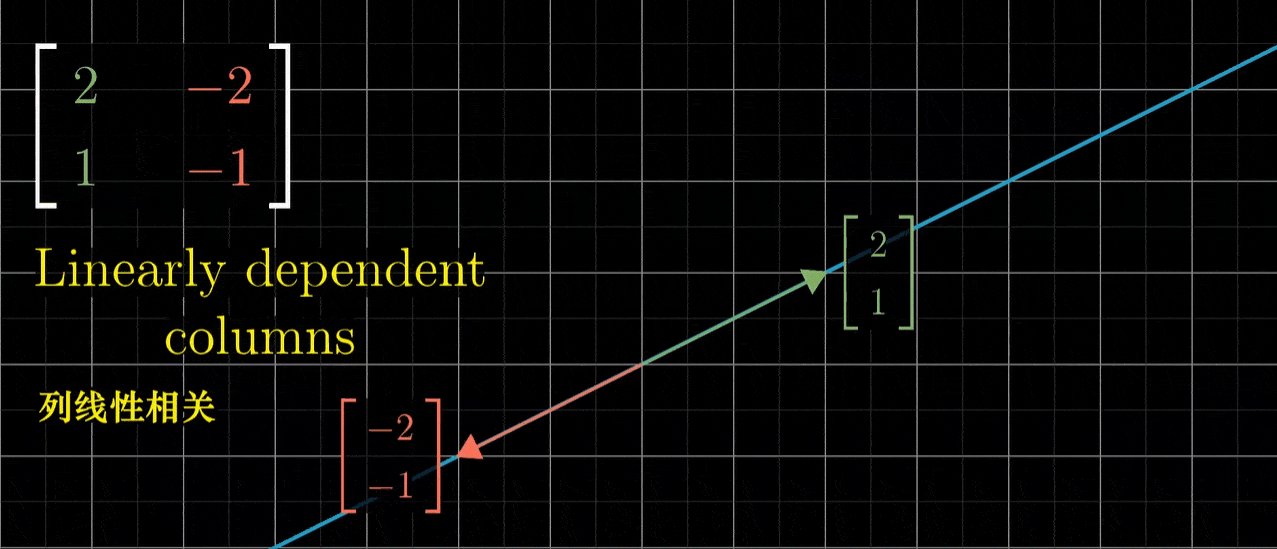
- 如果变换后的i帽和变换后的j帽是线性相关的,意味着其中一个向量是另一个的倍数,那么这个线性变换将整个二维空间挤压到它们所在一条直线上,也就是这两个线性相关向量所张成的一维空间
总结
- 线性变换是操纵空间的一种手段,它保持网格线平行且等距分布,并且保持原点不动
- 这种变换只需要几个数字就能描述清楚,这些数字就是变换后基向量的坐标
- 以这些坐标为列所构成的矩阵为我们提供了一种描述线性变换的语言,而矩阵向量乘法就是计算线性变换作用于给定向量的一种途径
- 这里重要的一点是,每当你看到一个矩阵时,你都可以把它解读为对空间的一种特定变换


