02-线性组合、张成的空间与基
数学需要的不是天赋,而是少量的自由想象,
但想象太过自由又会陷入疯狂。
—安古斯‧罗杰斯
基
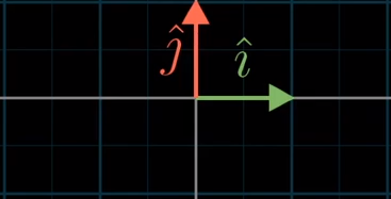
- 在xy坐标系中,有两个非常特别的向量。一个指向正右方,长度为1,通常被称为 “i帽” 或者x方向的单位向量;另一个指向正上方,长度为1,通常被称为 “j帽” 或者y方向的单位向量
- i帽和j帽两个向量有着特殊的名称,它们合起来被称为坐标系的基
- 严格定义:向量空间的一组基是张成该空间的一个线性无关向量的集合
线性组合
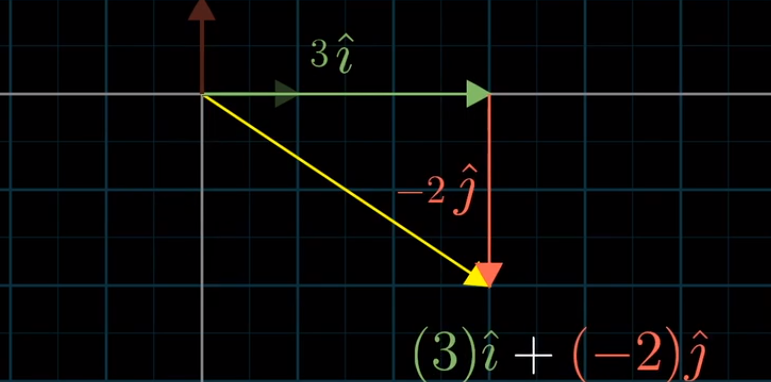
- 当看到一对描述向量的数时,比如(3,-2),把它的每个坐标看作一个标量,也就是说它们如何拉伸或压缩一个向量

- 现在想象向量(3,-2)的x坐标是一个标量,它将“i帽”拉伸为原来的3倍;y坐标也是一个标量,它将“j帽”反向并拉伸为原来的2倍。从这个角度去看,这个向量实际上是两个经过缩放的向量的和
- 当你把坐标看作标量时,基向量实际上就是这些标量缩放的对象
- 我们根据这两个特殊的基向量构建坐标系时,我们完全可以选择不同的基向量,获得一个合理的新坐标系
- 每当我们用数字描述向量时,它都依赖于我们正在使用的基
- 两个数乘向量的和被称为这两个向量的线性组合
张成的空间
二维空间
- 如果固定其中一个标量,让另一个标量自由变化,所产生的向量的终点会描出一条直线
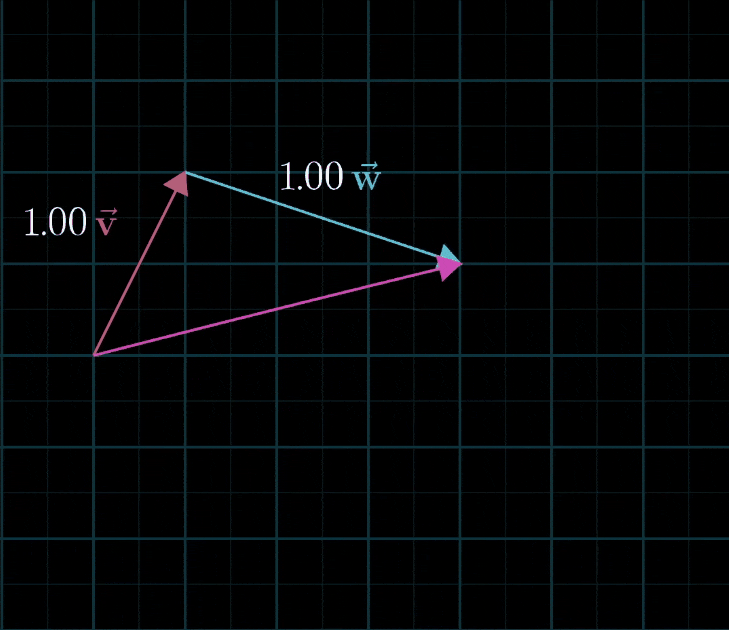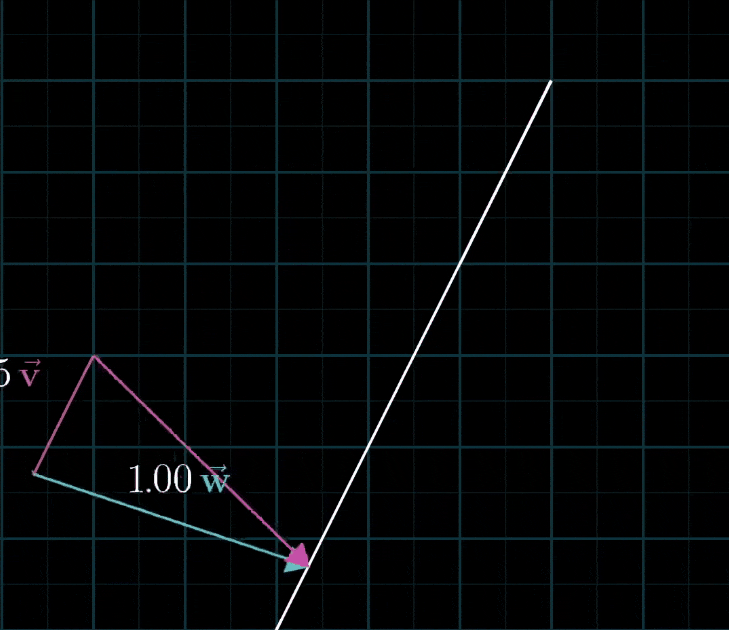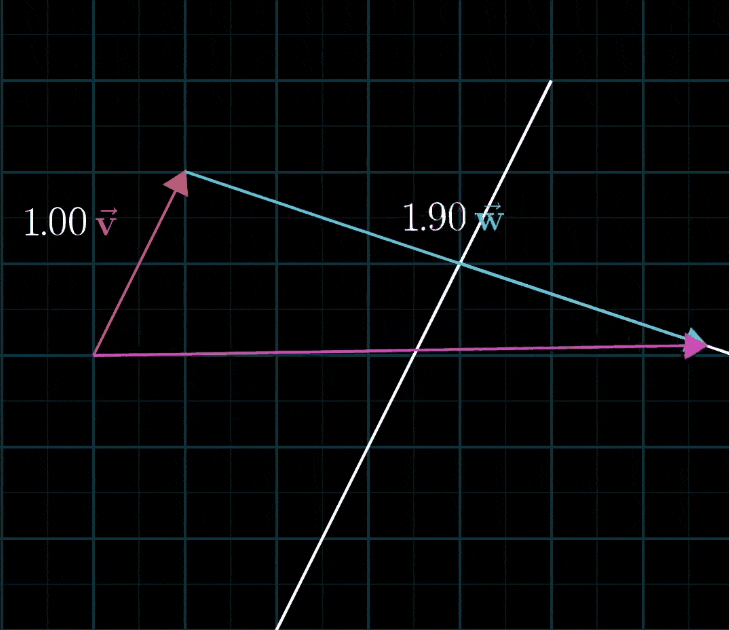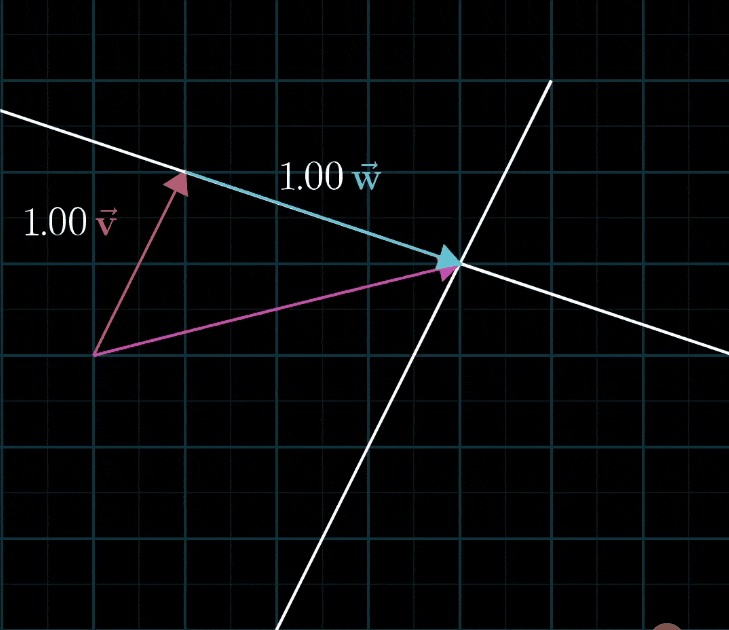
- 如果让两个标量同时自由变化,考虑所有可能得到的向量,可能有两种情况:
- 大部分情况下,对于一对初始向量,你能到达平面中的每一个点,所有二维向量都尽在掌握

- 但是也有糟糕的情况,当两个初始向量恰好共线时,所产生的向量的终点被限制在一条过原点的直线上
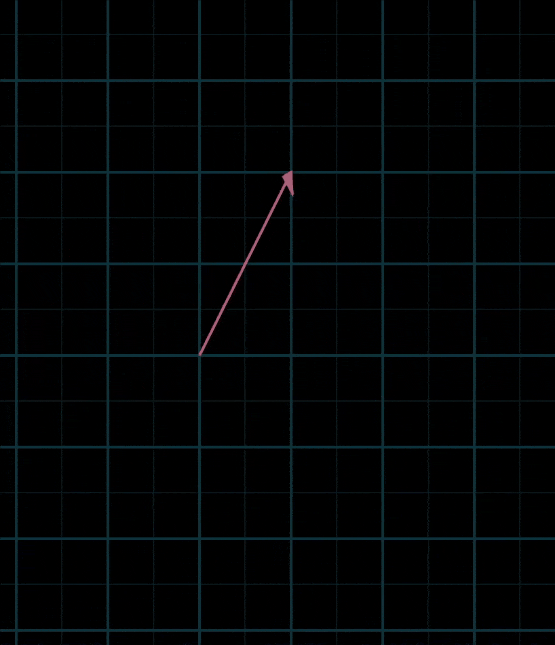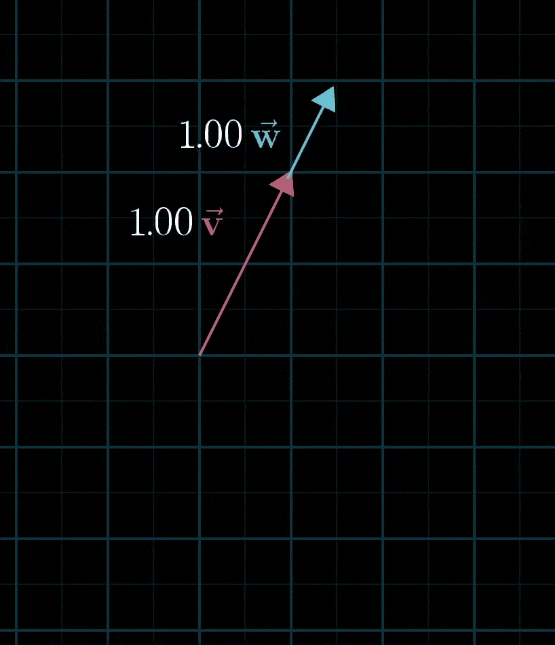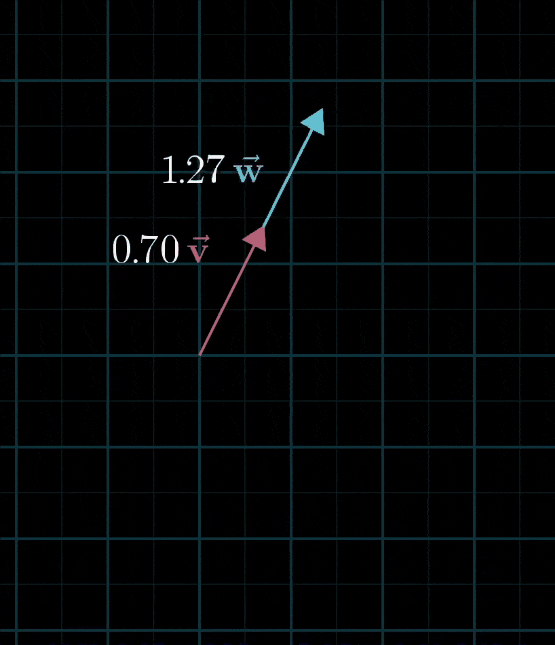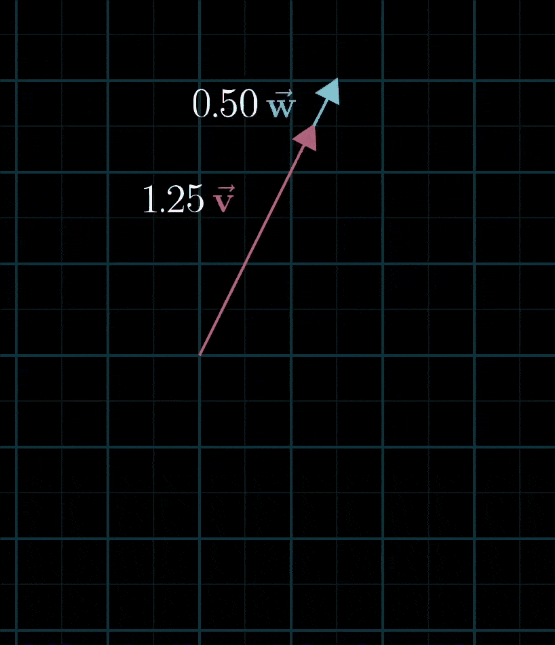
- 实际上还有第三种可能 : 两个向量都是零向量,那你就只能乖乖待在原点了

- 所有可以表示为给定向量线性组合的向量的集合,被称为给定向量张成的空间(span)
- 当你只考虑一个向量时,就把它看作箭头;当你考虑多个向量时,就把它们都看作点
- 对大部分二维向量对来说,它们张成的空间是所有二维向量的集合。但当共线时,它们张成的空间就是,终点落在一条直线上的向量的集合
三维空间
-
在三维空间中取两个指向不同方向的向量,它们张成的空间是什么?这两个向量张成的空间就是它们所有可能的线性组合,也就是缩放再相加之后所有可能得到的向量
-
大概可以想象一下,逐渐改变线性组合中的两个标量,把缩放后的向量相加,然后跟着最终向量的终点走,这个终点会画出三维空间中某个过原点的平面,这个平面就是这两个向量张成的空间,或者更确切的说,所有终点落在这个平面上的向量的集合是这两个向量张成的空间

- 选择三个标量,对三个向量分别进行缩放,然后把结果相加。三个向量所有可能的线性组合构成了它们张成的空间。这里会有两种情况:
-
如果第三个向量恰好落在前两个向量所张成的平面上,它们张成的空间并不改变,你还是被困在这个平面中。换句话说,在线性组合中引入第三个向量并没有让你 “走到更远”
-
但是如果你随机选一个向量,它几乎不可能落在前两个向量所张成的平面中。这种情况下,由于第三个向量指向不同的方向,我们就能得到所有的三维向量
- 可以这样思考,当你缩放第三个向量时,它将前两个向量张成的平面沿它的方向来回移动,从而扫过整个空间。另一种思考方式是,你完全利用了你掌握的自由变化的三个标量,从而得到空间中所有的三维向量
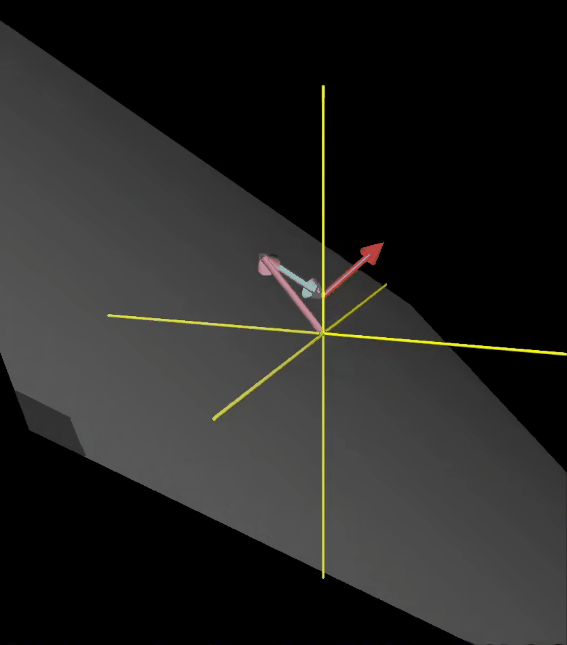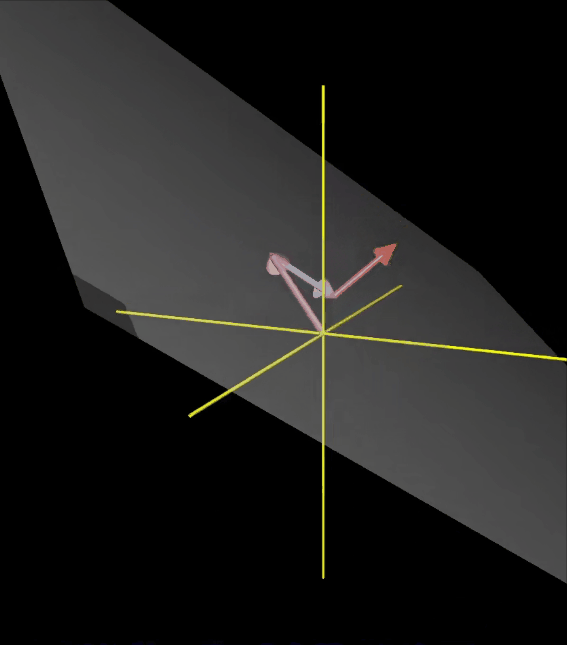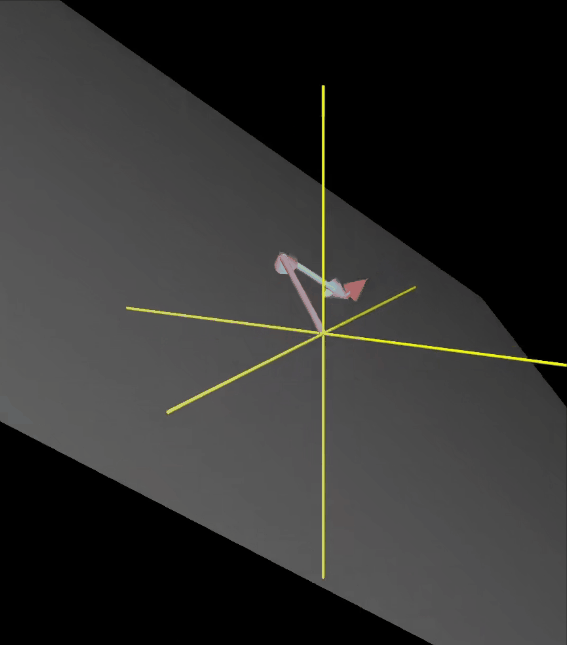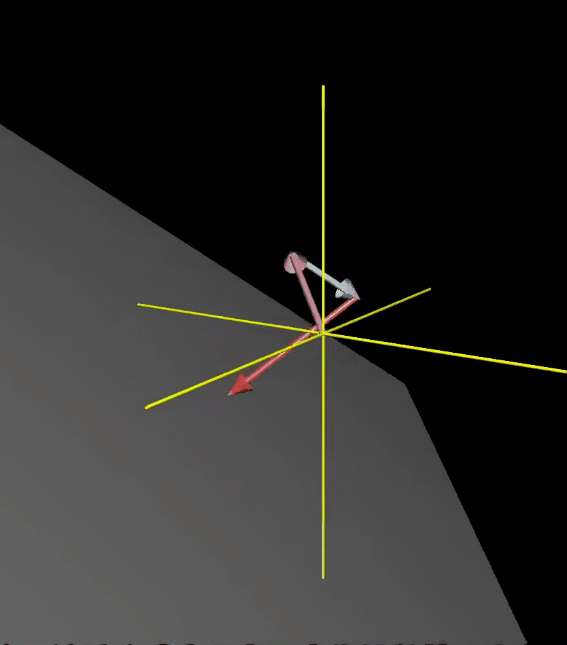
一些术语
-
你有多个向量,并且可以移除其中一个而不减小张成的空间,即一组向量中至少有一个是多余的,没有对张成空间做出任何贡献.当这种情况发生时,我们称它们是 “线性相关” 的。另一种表述方法是其中一个向量可以表示为其他向量的线性组合,因为这个向量已经落在其它向量张成的空间之中
-
另一方面,如果所有向量都给张成的空间增添了新的维度,它们就被称为是 “线性无关” 的


