重学数据结构之哈夫曼树
一、哈夫曼树
1.带权扩充二叉树的外部路径长度
扩充二叉树的外部路径长度,即根到其叶子节点的路径长度之和。
例如下面这两种带权扩充二叉树:
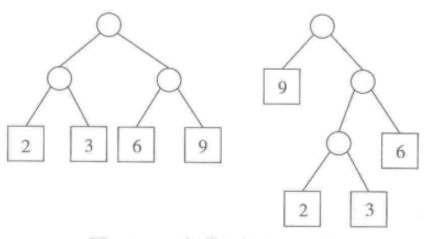
左边的二叉树的外部路径长度为:(2 + 3 + 6 + 9) * 2 = 38。
右边的二叉树的外部路径长度为:9 + 6 * 2 + (2 + 3) * 3 = 36。
2.哈夫曼树
哈夫曼树(Huffman Tree)是一种重要的二叉树,在信息领域有重要的理论和实际价值。
设有实数集 W = {W0 ,W1 ,···,Wm-1 },T 是一颗扩充二叉树,其 m 个外部节点分别以 Wi (i = 1, 2, n - 1) 为权,而且 T 的带权外部路径长度在所有这样的扩充二叉树中达到最小,则称 T 为数据集 W 的最优二叉树或者哈夫曼树。
二、哈夫曼算法
1.基本概念
哈夫曼(D.A.Huffman)提出了一个算法,它能从任意的实数集合构造出与之对应的哈夫曼树。这个构造算法描述如下:
- 算法的输入为实数集合 W = {W0 ,W1 ,···,Wm-1 }。
- 在构造中维护一个包含 k 个二叉树集合的集合 F,开始时k = m 且 F = {T0 ,T1 ,···,Tm-1 },其中每个 Ti 是一颗只包含权为 Wi 的根节点的二叉树。
该算法的构造过程中会重复执行以下两个步骤,直到集合 F 中只剩下一棵树为止:
- 构造一颗二叉树,其左右子树是从集合 F 中选取的两颗权值最小的二叉树,其根节点的权值设置为这两颗子树的根节点的权值之和。
- 将所选取的两颗二叉树从集合 F 中删除,把新构造的二叉树加入到集合 F 中。
注意:给定集合 W 上的哈夫曼树并不唯一!
2.示例
对于实数集合 W = {2, 1, 3, 7, 8, 4, 5},下面的图1到图7表示了从这个实数集合开始,构造一个哈夫曼树的过程:
图1:

图2:
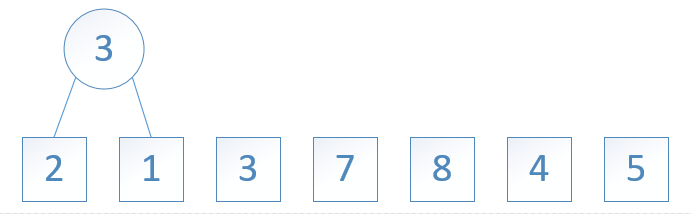
图3:
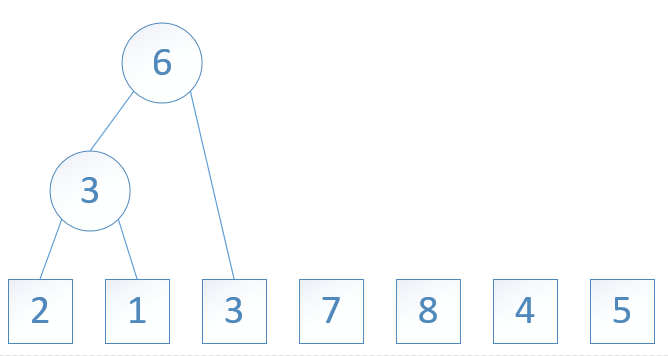
图4:
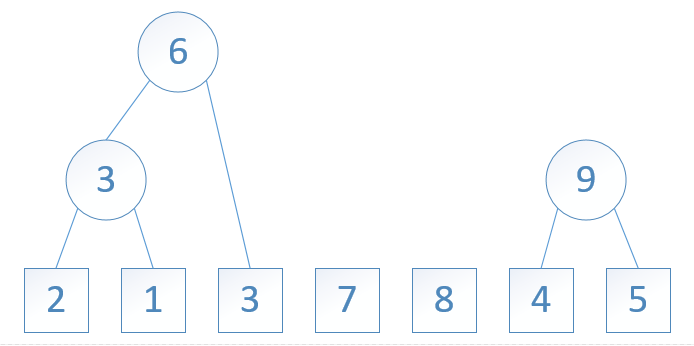
图5:
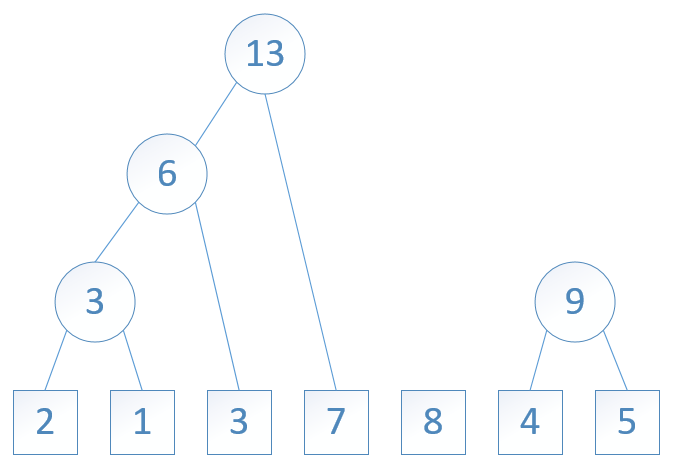
图6:
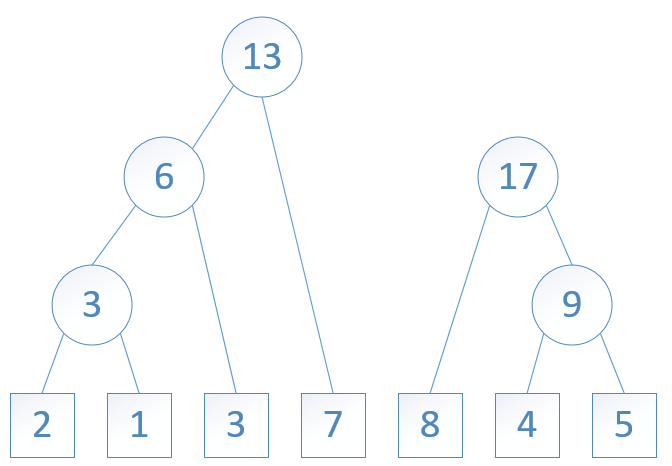
图7:
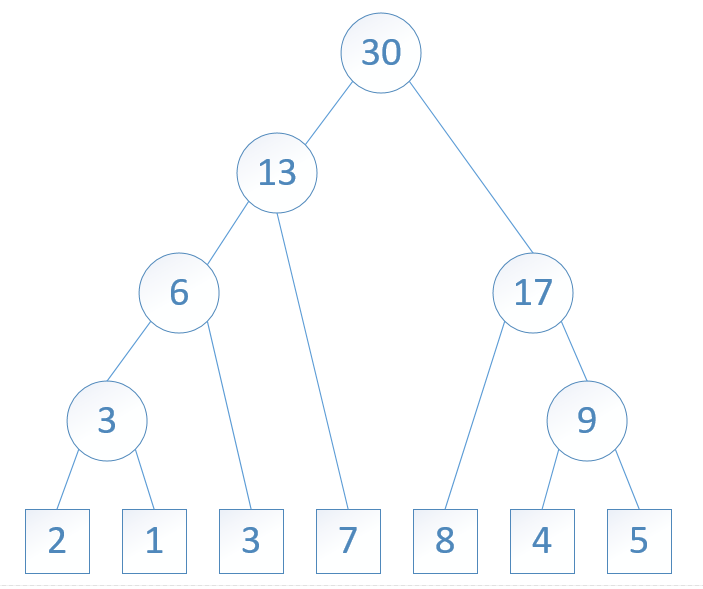
三、哈夫曼算法的实现
1.实现思路
要实现哈夫曼算法,需要维护一组二叉树,而且要知道每颗二叉树的根节点的权值 ,这个可以使用前面定义的二叉树的节点来构造哈夫曼树,只需要在根节点处记录该树的权值。而在执行算法时
在算法开始时,需要根据传入的实数集和来创建一组单节点的二叉树,并以权值作为其优先级存入一个优先级队列之中,在之后的过程中反复执行以下两步,直至队列中只有一颗二叉树:
1)从该优先级队列中取出两颗权值最小的二叉树;
2)创建一颗新的二叉树,其权值为选出的两棵树的权值之和,其左右子树分别为选出的两颗树,并将创建好的二叉树加入到优先级队列中。
当整个优先级队列中只剩下一颗二叉树的时候,就得到我们需要的哈夫曼树了。
2.实现代码
首先是要对哈夫曼树的节点进行定义,主要是增加一个权值,定义哈夫曼树节点的代码如下:
1 # 哈夫曼树节点 2 class HNode(Node): 3 def __init__(self, value=None, left=None, right=None, weight=None): 4 super(HNode, self).__init__() 5 self.value = value 6 self.left = left 7 self.right = right 8 self.weight = weight
然后还需要一个优先级的队列,在我前面写过的一篇队列的博客中有提到,只不过那篇博客里的优先级队列用的是一个最大堆,而在这里需要用最小堆,这样每次才能取出权值最小的树。
最后,下面就是实现哈夫曼算法的主要代码了:
1 def create(weights: list): 2 """ 3 根据传入的权值列表创建一个哈夫曼树 4 :param weights: 实数集合 5 """ 6 queue = PriorityQueue() 7 # 将节点添加到优先级队列中 8 for weight in weights: 9 node = HNode(weight=weight) 10 queue.enqueue(node, weight) 11 while queue.size() > 1: 12 node1 = queue.dequeue() 13 node2 = queue.dequeue() 14 new_node = HNode(left=node1, right=node2, weight=node1.weight + node2.weight) 15 queue.enqueue(new_node, new_node.weight) 16 return queue.dequeue()
四、哈夫曼编码问题
1.问题描述
最优编码问题,给定两个集合 C 和 W,C 为基本数据集合,W 为 C 中各个字符在实际信息传递中使用的频率,要求设定一套编码规则,要求: 1)使用这种编码规则的开销最小; 2)对任意一对不同字符 Ci 和 Cj,要求 Ci 的编码不是 Cj 编码的前缀。
2.问题分析
使用哈夫曼算法构建一颗哈夫曼树,这棵树的叶子节点的数量和字符数量一致,叶子节点的值就是字符的值,叶子节点的权值就是该字符对应的使用频率。然后从根节点开始遍历,往左子树遍历时标记为0,往右子树遍历时标记为1,这样就能保证走到叶子节点时所标记的路径结果是不一样的了,最后将每个叶子节点的值和对应的标记结果返回,就是题目所求的最优编码。
例如输入的数据为:{"A": 2, "b": 3, "c": 5, "d": 6, "e": 9} 。
则构造出来的哈夫曼树如下图:
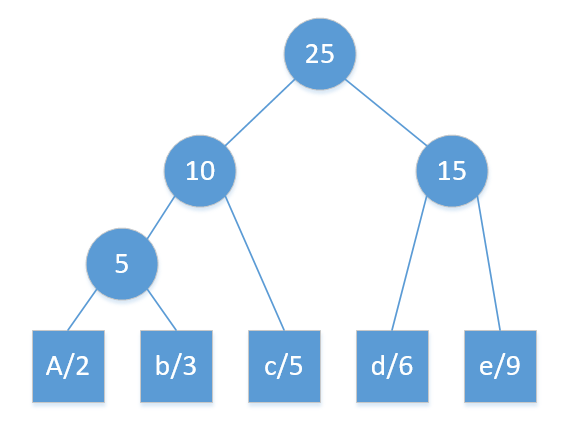
最后得到的编码为:{"A": "000", "b": "001", "c": "01", "d": "10", "e": "11"}
3.代码实现
下面就是使用哈夫曼算法来求解编码问题的主要代码了:
1 from Tree.tree import Node 2 from Queue.queue import PriorityQueue 3 4 5 # 哈夫曼树节点 6 class HNode(Node): 7 def __init__(self, value=None, left=None, right=None, weight=None): 8 super(HNode, self).__init__() 9 self.value = value 10 self.left = left 11 self.right = right 12 self.weight = weight 13 14 15 # 自定义哈夫曼树 16 class HuffmanTree: 17 def __init__(self): 18 self.root = HNode() 19 self.code = {} 20 21 def get_leaves(self, node: HNode, code: str): 22 """ 23 获取所有叶节点,对树中的分支节点向左子节点的路径标记为0,向右子节点的路径标记为1 24 :param node: 哈夫曼树的节点 25 :param code: 字符使用的编码 26 :return: 27 """ 28 if not node: 29 return 30 code_ = code # 因为要分别向左向右探索路径,所以需要复制一份 31 if node.left: 32 code += "0" 33 self.get_leaves(node.left, code) 34 if node.right: 35 code_ += "1" 36 self.get_leaves(node.right, code_) 37 # 没有左右子节点,表明是叶子节点 38 if not node.left and not node.right: 39 self.code[node.value] = code 40 41 def create(self, char_data: dict): 42 """ 43 根据传入的权值列表创建一个哈夫曼树 44 :param char_data: 字符和其对应频率的字典 45 """ 46 queue = PriorityQueue() 47 # 将节点添加到优先级队列中 48 for char, weight in char_data.items(): 49 node = HNode(value=char, weight=weight) 50 queue.enqueue(node, weight) 51 while queue.size() > 1: 52 node1 = queue.dequeue() 53 node2 = queue.dequeue() 54 new_node = HNode(left=node1, right=node2, weight=node1.weight + node2.weight) 55 queue.enqueue(new_node, new_node.weight) 56 self.root = queue.dequeue() 57 58 59 def solution(char_data: dict): 60 """ 61 解决哈夫曼编码问题 62 :param char_data: 字符和其对应频率的字典 63 :return: 64 """ 65 tree = HuffmanTree() 66 tree.create(char_data) 67 tree.get_leaves(tree.root, "") 68 return tree.code


 浙公网安备 33010602011771号
浙公网安备 33010602011771号