贝塞尔曲线生成及测试

玩过ps的同学，应该用过一个钢笔工具。

而钢笔产生的就是贝塞尔曲线。还有这里来体验一下：

https://myst729.github.io/bezier-curve/

 

Bezier曲线分为一次/二次/三次/多次贝塞尔曲线，之所以这么分是为了更好的理解其中的内涵。

一次贝塞尔曲线（线性Bezier），实际上就是一条连接两点的直线段。
二次贝塞尔曲线，就是两点间的一条抛物线，利用一个控制点来控制抛物线的形状。
三次贝塞尔曲线，则需要一个起点，一个终点，两个控制点来控制曲线的形状。
实例如下：在http://cubic-bezier.com/#.42,0,1,1的地方体验一下。

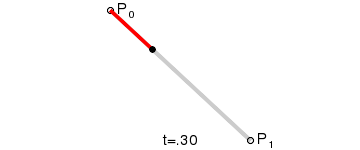
一阶曲线。

 

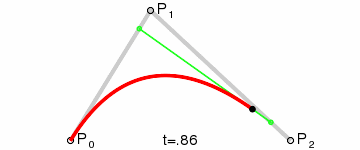
二阶的贝塞尔曲线是这样画出来的。

 

 

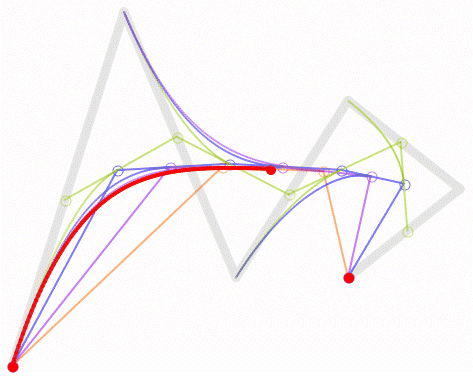
而多阶的是这样的。

 

 

那二阶的计算公式，其中 0<=t<=1。

　　二阶的计算点的公式： P0*(1-t)^2 + 2*P1*t(1-t) + P2*t^2 =P，其中P0为起始点，P1为控制点，P2为终点。那我们用matlab仿真，代码如下：

%% 起始点
startx=1;
starty=1;
%% 终止点
endx=10;
endy=0;
%% 控制点
cont1x=5;
cont1y=1;
%% 生成曲线
pointnum=100;%步数
t=1/(pointnum-1);
for i=1:pointnum-1
    x= startx*(1-i*t)^2 + cont1x*2*i*t*(1-i*t) + endx*(i*t)^2;
    y= starty*(1-i*t)^2 + cont1y*2*i*t*(1-i*t) + endy*(i*t)^2;
    hold on;
    plot(x,y,'.');
end

plot(startx,starty,'*')
plot(endx,endy,'*')
plot(cont1x,cont1y,'*')

 

 四个点的话就是两个控制点 p1,p2，另外两个就是起点和终点p0,p3。

公式为： P = P0*(1-t)^3 +3*P1*t*(1-t)^2+3*P2*(1-t)*t^2+P3*t^3 。

 

C++代码如下：

struct Point_Float
{
    float x;
    float y;
};

float MetaComputing(float p0, float p1, float p2, float p3, float t)
{
    // 方法一:
    float a, b, c;
    float tSquare, tCube;
    // 计算多项式系数
    c = 3.0 * (p1 - p0);
    b = 3.0 * (p2 - p1) - c;
    a = p3 - b - c - p0;

    // 计算t位置的点
    tSquare = t * t;
    tCube   = t * tSquare;
    return (a * tCube) + (b * tSquare) + (c * t) + p0;

    // 方法二: 原始的三次方公式
    //  float n = 1.0 - t;
    //  return n*n*n*p0 + 3.0*p1*t*n*n + 3.0*p2*t*t*n + p3*t*t*t;
}

float MetaComputing(float p0, float p1, float p2, float t)
{
    // 方法一:
    float a, b, c;
    float tmin;
    // 计算多项式系数
    c = p0;
    b = 2.0 * p1;
    a = p2;

    // 计算t位置的点
    tmin = 1-t;
    return (tmin*tmin*c) + (tmin*t*b) + (t*t*a);

}

Point_Float PointOnTrieBezier(Point_Float* cp, float t)
{
    Point_Float tPoint;
    tPoint.x = MetaComputing(cp[0].x, cp[1].x, cp[2].x, cp[3].x, t);
    tPoint.y = MetaComputing(cp[0].y, cp[1].y, cp[2].y, cp[3].y, t);
    return tPoint;
}

Point_Float PointOnCubeBezier(Point_Float* cp, float t)
{
    Point_Float tPoint;
    tPoint.x = MetaComputing(cp[0].x, cp[1].x, cp[2].x, t);
    tPoint.y = MetaComputing(cp[0].y, cp[1].y, cp[2].y, t);
    return tPoint;
}

 

 

参考资料：　　　　

http://blog.csdn.net/cdnight/article/details/48468653

https://www.cnblogs.com/cheneasternsun/p/5941438.html

http://blog.csdn.net/devillixin/article/details/39896355