【算法•日更•第四十八期】二分图(匈牙利算法)
▎前言
小编最近看来hza大佬的博客,也来写一篇匈牙利算法的博客。
小编决定写的不一样点。
▎前置知识
二分图的基础知识。
▎匈牙利算法
☞『引入』
匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法,并推动了后来的原始对偶方法。美国数学家哈罗德·库恩于1955年提出该算法。此算法之所以被称作匈牙利算法,是因为算法很大一部分是基于以前匈牙利数学家Dénes Kőnig和Jenő Egerváry的工作之上创建起来的。
设
是一个无向图。如顶点集V可分割为两个互不相交的子集
,选择这样的子集中边数最大的子集称为图的最大匹配问题(maximal matching problem)。如果一个匹配中,
且匹配数
,则称此匹配为完全匹配,也称作完备匹配。特别的当
称为完美匹配。(copy自百度)
☞『匹配边与非匹配边』
如果你已经会了二分图的基础知识,那么你一定知道二分图中有匹配这个东西,有匹配边,那么剩下的不就是不匹配的边了吗?我们称之为非匹配边。
☞『交替路』
这个东西分开看。
先来说路,路正如其名,没什么可说的,就是路径的意思。
那么什么是交替路呢?最大匹配是只能走匹配边,但是它却反其道而行之,是匹配边 -> 非匹配边 -> 匹配边 -> 非匹配边 -> 匹配边 -> 非匹配边 -> ……
就是这样交替下去,所以才叫交替路。
例如下面的这条红边就是交替路:
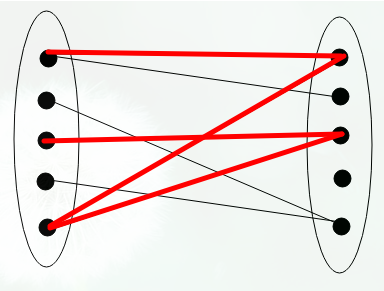
☞『增广路』
听见这个名字好像想起了什么,对!网络流,看看有没有什么相似的地方。
增广路就是从未匹配的点出发寻找交替路,且遇到未匹配的点。
☞『算法核心』
其实就是不断找增广路,每找到一条就更新一次,直到没有增广路。


