【算法•日更•第三十三期】网络流基础知识（最大流）

▎写在前面

　　小编早就听说过了网络流这种神奇的东西，一直以为很高端大气上档次，但是很难，就没学。

　　今日一见也不过如此，一点也不高端，不大气，不上档次。

▎网络流

☞『定义』

　　网络流(network-flows)是一种类比水流的解决问题方法，与线性规划密切相关。网络流的理论和应用在不断发展，出现了具有增益的流、多终端流、多商品流以及网络流的分解与合成等新课题。网络流的应用已遍及通讯、运输、电力、工程规划、任务分派、设备更新以及计算机辅助设计等众多领域。（copy自百度）

☞『介绍』

　　其实上面的度娘写的定义一点也不易懂，主要就是自来水问题：

　　

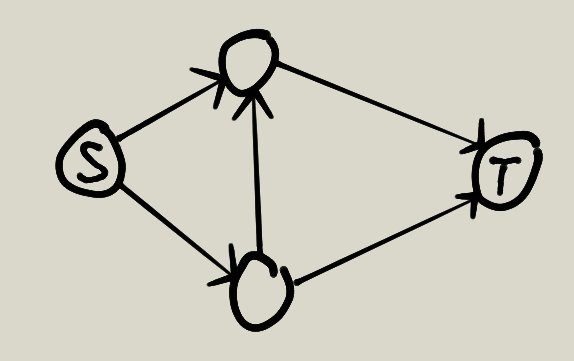
　　其中S是起点，T是终点，这是一个有向图，所以你会发现边都是有方向的。

　　当然，每条边都是有权值的，也就是单位时间内的流量，S中有无限的水，但是不可能在单位时间内全部运送到终点T，此时的问题就是单位时间内最多能流过多少水，到达T？

　　其实网络流问题只是一个大的标题，具体分下来有最大流，费用最小流等等，上面的问题就是最经典的最大流问题，当然，这篇博客也只会讲最大流。

☞『专业名词』

　　源点：S点就是源点，也就是我们刚才所说的起点。

　　汇点：T点是汇点，正如其名，是流所交汇的地方。

　　容量：每条边的权值就是这条边的容量。

☞『一些规则』

　　容量限制：一条边流过的量不可能超过它的容量。

　　斜对称：一条边(u,v)的容量等于这条边反过来的容量的相反值。比如说这条边容量是正1000，虽然它的反向边不存在，但是我们把它认为是负1000。

　　流守恒：就是说一个点流入多少，那么就会流出多少。（除了源点和汇点）

▎操作：增广

　　增广是最大流求解的基础操作。

　　比如说这是我们的图：

　　

　　刚开始的时候要维护反向边，初始为0，所以就先不画出来，我们先进行搜索，找到T。

　　

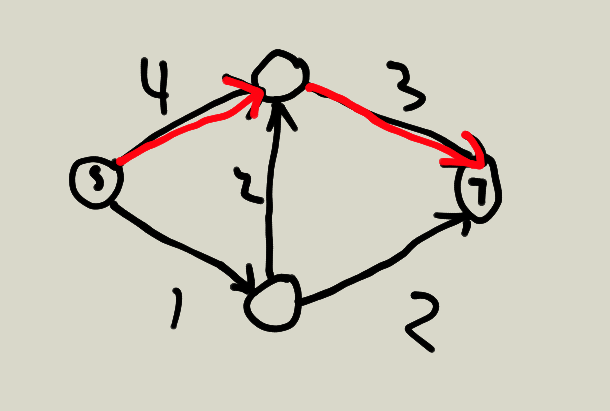
　　其中最短的边长为3，那么这条边的边长全部减去3，同时反向边都加三，最大流增加3。

　　然后就是这个样子的：

　　

　　就这样一直反复操作下去，直到到不了T，此时加起来的值就是最大流。