【算法•日更•第二十九期】基础多项式

▎前言

　　小编相当的菜，这篇博客难度稍高，所以有些可能不会带有证明，博客中更多的是定义。

　　我们将要学到的东西：

• 环和域
• 多项式
• 卷积
• 多项式乘法
• 多项式点值表示
• 多项式的根
• 单位根

▎环和域

　　先来说什么是域。

　　简单的说，很多数字他们在一起能保证互相加减乘除这群数字中的数，仍能得到这群数字中的数（运算封闭），那么这些数字称为域。

　　当然，域中的数字通常是无限多个的。

　　那么环是什么，对比来看，域支持加减乘除运算封闭，而环只支持加和乘运算封闭。

　　也就是说域属于环，而域是特殊的环。

　　正因为域的特殊，所以域具有更多的性质，所以我们之后研究的多项式均与域相关，所以环在本篇博客中不是很重要。

　　常见域与环举例：

　　常见域：有理数域Q，实数域R，复数域C都是域。

　　常见环：整数集就是环。

　　因为整数集中除法是不封闭的，因为整数除以整数说不定会有小数，而小数不属于整数。

▎多项式

　　设R是一个环，a₀，a₁，…，a_n都是R中的元素，且a_n≠0，规定x⁰=1，那么我们把：

　　

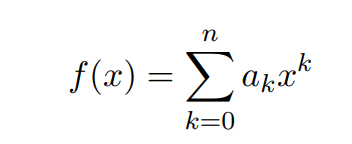
　　称为R上n次多项式。

　　这个多项式是在环上定义的，但是我们后续使用的多项式，一律是域上的多项式。

▎卷积

　　数字与数字的乘法的结果叫做积。

　　而向量乘向量的结果叫做卷积。

　　那么什么是向量，如果你不想知道就看下一段（对后续内容没有妨碍），向量就是有方向的量，也就是说这种量不仅有数字那样的值，也有方向。如平面直角坐标系中的坐标，就是向量（方向就是原点到这个点的方向）。

　　当然，向量可以存很多个数，类似于数组，所以之后提到的向量a，b，如果没有特殊说明，可以认为是多项式a和多项式b的系数存储的数组。

　　利用我们平时多项式乘多项式的过程，我们可以得出以下结论：

　　对于向量a，b，令

　　

　　那么c就是向量a与b的积（这只是个定义，不需要证明什么的）。

▎多项式乘法

　　设这里有两个多项式f(x)和g(x)（项数分别是n和m），那么我们易得：

　　

　　其中c是a与b的卷积。

　　显然，直接计算的时间复杂度是O(nm)。

▎多项式点值表示

　　我们先来思考：多项式的表示方法有几种？

　　两种，一种是系数表示法，一种是点值表示法。

　　系数表示法：按照一定的顺序（例如按x的次数升序）排列，那么我们只要知道每一项对应的系数，那么我们就可以确定唯一的多项式。

　　点值表示法：我们可以取一个x的值并带入，就会得到唯一的f值，就像函数一样，我们需要n+1对点对( x_k, f(x_k) )就可以确定唯一的多项式f(x)。

　　知道了点值表示法后，我们设f(x), g(x) 为次数分别为 n, m 的多项式，那么就有n+m+1个互 不相同的点 x₀, x₁, . . . , x_n+m。

　　若我们已经知道了f(x), g(x)，那么我们就可以以较少的时间复杂度得到f(x) g(x)，当然，加法也是这样。

▎多项式的根

　　设域F属于域K，f(x)是F上的多项式，α是K中的元素，若f(α)=0，那么我们称α为f(x)的一个根。

　　因此f(x)的根不一定在F中。

▎单位根

　　多项式xⁿ−1的根称为n次单位根。