【算法•日更•第十八期】信息奥赛一本通1600：【例 4】旅行问题题解
废话不多说，直接上题：
1600：【例 4】旅行问题
时间限制: 1000 ms 内存限制: 524288 KB
提交数: 96 通过数: 36
【题目描述】
原题来自：POI 2004
John 打算驾驶一辆汽车周游一个环形公路。公路上总共有 n 车站，每站都有若干升汽油（有的站可能油量为零），每升油可以让汽车行驶一千米。John 必须从某个车站出发，一直按顺时针（或逆时针）方向走遍所有的车站，并回到起点。在一开始的时候，汽车内油量为零，John 每到一个车站就把该站所有的油都带上（起点站亦是如此），行驶过程中不能出现没有油的情况。
任务：判断以每个车站为起点能否按条件成功周游一周。
【输入】
第一行是一个整数 n，表示环形公路上的车站数；
接下来 n 行，每行两个整数 pi,di ，分别表示表示第 i 号车站的存油量和第 i 号车站到下一站的距离。
【输出】
输出共 n 行，如果从第 i 号车站出发，一直按顺时针（或逆时针）方向行驶，能够成功周游一圈，则在第 i 行输出 TAK，否则输出 NIE。
【输入样例】
5 3 1 1 2 5 2 0 1 5 4
【输出样例】
TAK NIE TAK NIE TAK
【提示】
数据范围与提示：
对于全部数据，3≤n≤106,0≤pi≤2×109,0<di≤2×109 。
【来源】
这道题先不管其他的，先来说怎么处理这个绕圈（环）的问题。
当然这是很简单的，只要破环成链就可以了，方法很粗暴，直接开到二倍就可以了。
什么意思呢？比如说数据是1，2，3，4，5的环，那么我们就可以改成1，2，3，4，5，1，2，3，4，5的链，这样任何的搭配方式都可以体现出来，只要注意不要多出来就可以了。
好了，回归这道题，如何解决？方法有三种：
方法1：直接暴力，模拟旅行的过程
显然，时间复杂度是O(n2)的，像这道题的超大的数据规模，肯定无法接受。
方法2：使用堆来优化
为什么上面的办法不行？因为我们没有合理的利用已经算过的东西。而且题目中涉及到了p和d，我们不妨合并成一个a数组，使a[i]=p[i]-d[i]，表示油量的增减情况。
我们可以维护一个前缀和pre来存储，那么我们要走的路就可以通过差分来求出，我们要判断一条路能否走成功，那么就要看这条路中油最少的情况是否大于0。
那么我们就可以使用堆来存储，整个算法时间复杂度是O(n log n)，但是对于这么大的数据规模来说还是太勉强。
方法3：还有其他方法，例如RMQ，不过小编不会
方法4：单调队列优化动态规划
虽然我看不出来哪里有动态规划，但是单调队列是必须要用的，我们可以把2*n-1当作n，把n当作k，把每一次到加油站的油当作数，这样就是单调队列的模板（定长连续子区间的最值问题）。
不过这些都很easy，但是怎样能够处理顺时针和逆时针呢？
这是一个棘手的问题，先来看下面的示例，比方说数据是这样的：
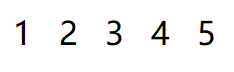
那么逆时针的顺序就是这样的：
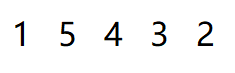
经过探寻规律得：p1[i]=p[n-i+2],d1[i]=d[n-i+1]，只要这样处理后就可以像顺时针一样再算了。
不过要注意边界值，p1[1]=1,d1[1]=d[n]，不信你试试，按上面算出来的会有问题。
详见注释，代码如下：
#include<iostream> using namespace std; long long n,p[3000000],d[3000000],pre[3000000],num[3000000],a[3000000],q[3000000],ans[3000000],p1[3000000],d1[3000000]; long long number(long long x)//判断逆时针前的位置 { if(x==n) return 1; else return 2*n-x+1; } inline void change()//改成逆时针 { p1[1]=p[1];d1[1]=d[n]; a[1]=p1[1]-d1[1]; pre[1]=a[1]; for(long long i=2;i<=n;i++) { p1[i]=p[n-i+2]; d1[i]=d[n-i+1]; a[i]=p1[i]-d1[i]; a[i+n]=a[i]; pre[i]=pre[i-1]+a[i]; } for(long long i=n+1;i<=2*n;i++) pre[i]=pre[i-1]+a[i]; } inline void dp() { long long head=1;long long tail=0; for(long long i=1;i<=2*n-1;i++)//顺时针 { while(num[head]<i-n+1&&head<=tail) head++; while(pre[i]<=q[tail]&&head<=tail) tail--; q[++tail]=pre[i]; num[tail]=i; if(i>=n) { if(q[head]-pre[i-n]<0) ans[i-n+1]=0; else ans[i-n+1]=1; } } change(); head=1;tail=0; for(long long i=1;i<=2*n-1;i++)//逆时针 { while(num[head]<i-n+1&&head<=tail) head++; while(pre[i]<=q[tail]&&head<=tail) tail--; q[++tail]=pre[i]; num[tail]=i; if(i>=n) if((q[head]-pre[i-n])>=0) ans[number(i)]=1; } } int main() { cin>>n; for(long long i=1;i<=n;i++) { cin>>p[i]>>d[i]; a[i]=p[i]-d[i]; a[i+n]=a[i]; pre[i]=pre[i-1]+a[i];//记录前缀和 } for(long long i=n+1;i<=2*n;i++) pre[i]=pre[i-1]+a[i]; dp(); for(long long i=1;i<=n;i++) if(ans[i]==1) cout<<"TAK"<<endl; else cout<<"NIE"<<endl; return 0; }
