【算法•日更•第十五期】信息奥赛一本通1594:涂抹果酱题解
废话不多说,直接上题:
1594:涂抹果酱
时间限制: 1000 ms 内存限制: 524288 KB
提交数: 146 通过数: 46
【题目描述】
Tyvj 两周年庆典要到了,Sam 想为 Tyvj 做一个大蛋糕。蛋糕俯视图是一个 N×M 的矩形,它被划分成 N×M 个边长为 1×1 的小正方形区域(可以把蛋糕当成 N 行 M 列的矩阵)。蛋糕很快做好了,但光秃秃的蛋糕肯定不好看!所以,Sam 要在蛋糕的上表面涂抹果酱。果酱有三种,分别是红果酱、绿果酱、蓝果酱,三种果酱的编号分别为 1,2,3。为了保证蛋糕的视觉效果,Admin 下达了死命令:相邻的区域严禁使用同种果酱。但 Sam 在接到这条命令之前,已经涂好了蛋糕第 K 行的果酱,且无法修改。
现在 Sam 想知道:能令 Admin 满意的涂果酱方案有多少种。请输出方案数 mod 106 。若不存在满足条件的方案,请输出 0。
【输入】
输入共三行。
第一行:N,M;
第二行:K;
第三行:M 个整数,表示第 K 行的方案。
字母的详细含义见题目描述,其他参见样例。
【输出】
输出仅一行,为可行的方案总数。
【输入样例】
2 2 1 2 3
【输出样例】
3
【提示】
样例说明:
| 方案一 | 方案二 | 方案三 |
| 2 32 3 | 2 32 3 | 2 32 3 |
| 1 21 2 | 3 13 1 | 3 23 2 |
数据范围与提示:
对于 30% 的数据,1≤N×M≤20;
对于 60% 的数据,1≤N≤1000,1≤M≤3;
对于 100% 的数据,1≤N≤10000,1≤M≤5。
【来源】
这道题和上一次的题目十分相像,可以直接判定这是状态压缩动态规划。
那么怎么状态压缩呢?这个果酱有三种颜色,所以我们就不能使用二进制了,而是采用三进制的方法状态压缩。
题目中的果酱有红绿蓝三色,那么我们就分别让他们用0,1,2来表示。
那么肯定要预处理,只要枚举好一行所有的状态即可,注意有些二进制的方法要变的,详见代码。
先来说状态怎么设计,我们可以用f[i][j]来表示第i行状态为a[j],值为状态是否可行。总之先分析一下现在这张图是什么样的。

其中第k行已经被涂过了,然后我们就可以分成这三个部分,分别是上图所示的三个部分(红绿蓝)。
因为第k行已经被涂过了,所以可以把它看成是第0行。显然,这样蓝色部分和红色部分第i行的方案数是一样的(因为互相不受干扰)。
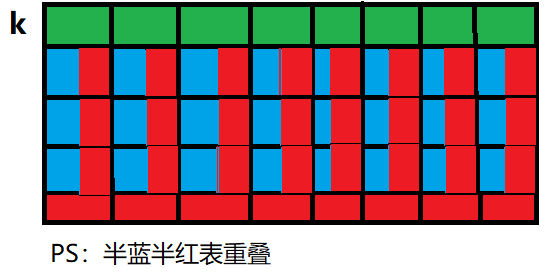
忽略小编拙劣的画技。
因此我们便利的行数只要是红色的行数就可以了,那么我们已经区分开了两个部分,怎样状态转移呢?
显然,f[i][j]=sum{f[i-1][k]},(前提是不发生冲突)其中a[j]是当前行的状态,a[k]是上一行的状态,那么这一行的方案数自然就是上一行方案数的和呗。
最后,我们要把所有状态的方案数都要加在一起,同时注意两个部分分别处理,方案总数是两个部分方案数的积。(乘法原理)
好了,详见注释,代码如下:
1 #include<iostream> 2 #define mod 1000000 3 using namespace std; 4 long long n,m,K,c[10000],cnt,a[10000],f[10001][200],s,num,correct[10000][10000],ans1,ans2; 5 inline int check(int x)//判断行内冲突 6 { 7 for(int i=m-1;i;i--) 8 if((x%c[i+1]/c[i])==(x%c[i]/c[i-1])) 9 return 0; 10 return 1; 11 } 12 inline int check2(int x,int y)//判断两行间的冲突 13 { 14 for(int i=m-1;i>=0;i--) 15 if((x%c[i+1]/c[i])==(y%c[i+1]/c[i])) 16 return 0; 17 return 1; 18 } 19 int main() 20 { 21 cin>>n>>m>>K;c[0]=1; 22 for(int i=1;i<=m;i++) 23 { 24 cin>>s; 25 num*=3; 26 num+=s-1;//三进制表示 27 c[i]=c[i-1]*3;//c是表示3进制数位的数组 28 } 29 if(!check(num)){cout<<0;return 0;}//如果第K行有冲突,那么直接输出0 30 for(int i=0;i<c[m];i++)//逐个枚举一行的状态 31 { 32 if(check(i)) a[++cnt]=i;//记录状态 33 if(i==num) f[0][cnt]=1;//初始化 34 } 35 for(int i=1;i<=cnt;i++)//枚举当前行状态 36 for(int j=1;j<=cnt;j++)//枚举上一行状态 37 if(check2(a[i],a[j])) correct[i][j]=1;//判断是否发生冲突 38 int x=max(K-1,n-K);int y=min(K-1,n-K);//分成两个部分 39 for(int i=1;i<=x;i++)//枚举行 40 for(int j=1;j<=cnt;j++)//枚举当前行状态 41 for(int k=1;k<=cnt;k++)//枚举上一行状态 42 if(correct[j][k]) f[i][j]=(f[i][j]+f[i-1][k])%mod;//注意是否发生冲突 43 for(int i=1;i<=cnt;i++)//枚举状态数 44 { 45 ans1+=f[x][i]; 46 ans1%=mod; 47 ans2+=f[y][i];//两个部分分别处理 48 ans2%=mod; 49 } 50 cout<<ans1*ans2%mod;//乘法原理 51 return 0; 52 }


