【算法•日更•第十四期】信息奥赛一本通1592：【例 1】国王题解

　　废话不多说，直接上题：

---

1592：【例 1】国王

时间限制: 500 ms         内存限制: 65536 KB
提交数: 290     通过数: 111 

【题目描述】

原题来自：SGU 223

在 n×n 的棋盘上放 k 个国王，国王可攻击相邻的 8 个格子，求使它们无法互相攻击的方案总数。

【输入】

只有一行，包含两个整数 n 和 k。

【输出】

每组数据一行为方案总数，若不能够放置则输出 0。

【输入样例】

3 2

【输出样例】

16

【提示】

样例输入 2

 

4 4

 

样例输出 2

 

79

 

数据范围与提示：

对于全部数据，1≤n≤10,0≤k≤n² 。

【来源】

无

　　不得不说，这道题太像还是n皇后了。详见此题链接：戳这里哦~

　　只不过是皇后变成了国王、地图上没有了坑而已。

　　不过我们可以先看一看数据规模，我一下子就被惊到了。n只有10，k只有100，但是虽然数据小，但是搜索要真的一个一个搜起来，那可就真的是指数级复杂度，肯定不行。 

　　于是我们就不得不选择优化，这道题属于状态压缩类动态规划，在不久前小编就已经使用过了，其实说白了就是使用二进制优化。

　　众所周知，二进制是这样的：1010110，一堆0和1，但是如果你的地图是由0、1组成的，那么就可以这样优化。

　　图解一下：

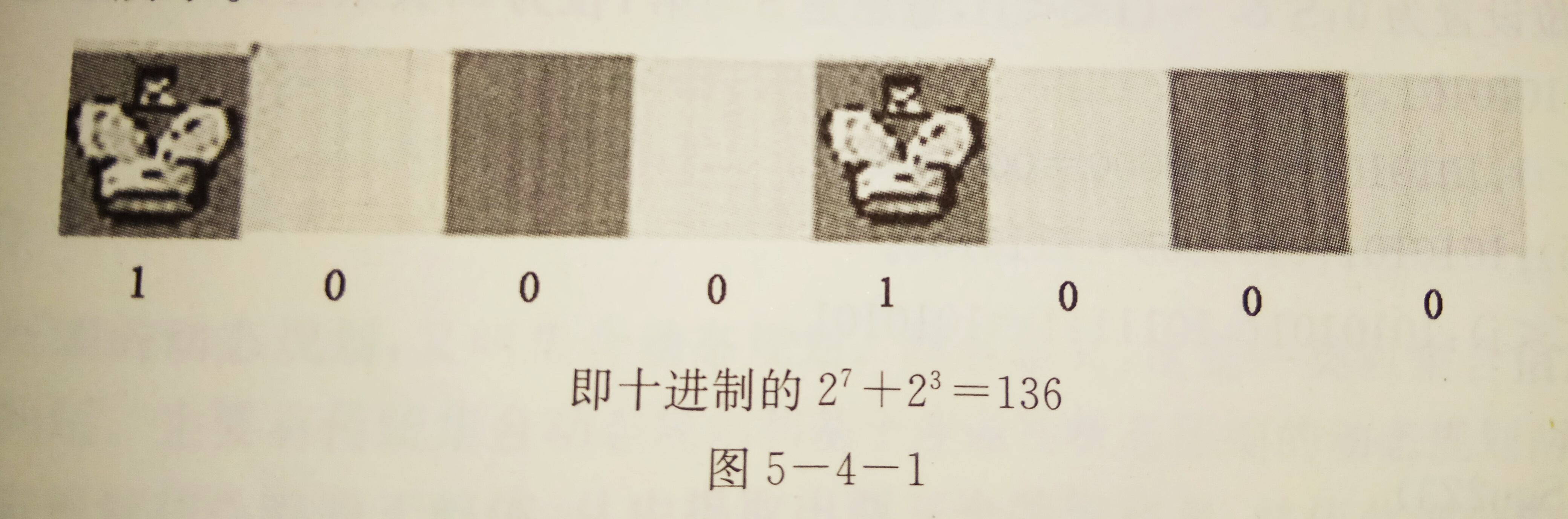
　　其实是从一本通提高篇上copy下来的。

　　那么一行的数据就浓缩成一个数了，那么我们在处理1时就只要用lowbit原理x&-x就可以找到最高位的1了（别问我为什么，别的大佬都不太清楚)。

　　好了，回归正题，这道题是动态规划题，那么怎样设计状态呢？

　　我们要在n*n的棋盘上放k个国王，那么我们不妨用f[i][j][k]来表示第i行的状态是a[j]（二进制表示），目前为止放了k个棋子。

　　显然f[i][j][k]=sum{i-1,l,k-num[j]}(不发生冲突)，其中l是，枚举上一行状态的变量，num[j]是a[j]这一状态可以放置的国王数。

　　行了，其他的都看注释吧，要不然不好解释，代码如下：

#include<iostream>
using namespace std;
long long n,K,num[1000],a[1000],sum,ans,f[300][300][300];
void pre()
{
    int cnt=0;//记录方案数 
    for(int i=0;i<(1<<n);i++)//注意，这里模拟的是一行的所有状态，而不是行数 
    {
        if(i&(i<<1)) continue;//如果结果不是0，那么就会有1是挨着的，不合法 
        cnt=0;
        for(int j=0;j<n;j++) if((1<<j)&i) cnt++;//如果i的二进制表示下的j位有1，那么就记录 
        a[++sum]=i;//记录状态 
        num[sum]=cnt;//记录可以放国王的数量 
    }
}
void dp()
{
    f[0][1][0]=1;//显然第0行第一位上可以放一个国王 
    for(int i=1;i<=n;i++)
    for(int j=1;j<=sum;j++)
    for(int k=0;k<=K;k++)
    {
        if(k>=num[j])//先看能不能减 
        for(int l=1;l<=sum;l++)
        if(!(a[l]&a[j]) && !(a[l]&(a[j]<<1)) && !(a[l]&(a[j]>>1)))//看看国王和上一行的国王起不起冲突 
        f[i][j][k]+=f[i-1][l][k-num[j]];
    }
    for(int i=1;i<=sum;i++) ans+=f[n][i][K];//最后一行的所有状态都要加上 
    cout<<ans;
}
int main()
{
    cin>>n>>K;
    pre();dp();
    return 0;
}