【算法•日更•第十一期】信息奥赛一本通1581：旅游规划题解

　　废话不多说，直接上题：

1581：旅游规划

时间限制: 1000 ms 内存限制: 524288 KB
提交数: 73 通过数: 39

【题目描述】

W 市的交通规划出现了重大问题，市政府下定决心在全市各大交通路口安排疏导员来疏导密集的车流。但由于人员不足，W 市市长决定只在最需要安排人员的路口安排人员。

具体来说，W 市的交通网络十分简单，由 $n$

经过长期调查，结果显示，如果一个交叉路口位于 W 市交通网最长路径上，那么这个路口必定拥挤不堪。所谓最长路径，定义为某条路径 $p = (v_{1}, v_{2}, v_{3}, \dots, v_{k})$

【输入】

第一行一个整数 $n$

之后 $n - 1$

【输出】

输出包括若干行，每行包括一个整数——某个位于最长路径上的路口编号。为了确保解唯一，请将所有最长路径上的路口编号按编号顺序由小到大依次输出。

【输入样例】

【输出样例】

【提示】

数据范围与提示：

对于全部数据， $1 \leq n \leq 2 \times 10^{5}$

【来源】

无

　　评价一下：一道极度恶心的树（shen）型（du）动（you）态（xian）规（sou）划（suo）题。

　　首先先来分析题目：题目告诉有n个路口，n-1条街道，这便会使我们想到一种数据结构：树。多么巧合，树也是n个节点，n-1条边，多一条就成了图了，这就暗示了我们要使用树型动态规划。

　　（错误示例）而小编偏不，小编首先想到了图的最短路径算法，既然是树，那么两点间的距离不就是固定的，a到b间的最短路径不就是最长路径吗？这还不好办，一个floyed，中间顺带记录下k完事。

　　结果一个超时，若干答案错误。

　　于是小编便退求其次，看看能不能用树型动态规划，毕竟这是树型动态规划分类里的练习题，可是死活找不到状态转移方程，甚至连设计状态都不行。

　　哎，下下策，看别人博客，结果发现都没有用动态规划，全都是用的搜索（没有任何记忆化，所以不属于记忆化搜索），小编只想吐槽一句，一本通里的题千万不要被分类所骗，上次的加分二叉树就在这个分类，却属于区间动态规划，这道题又……

　　不说了，回归正题：

　　决定好要搜索了，那么我们就要来思考一下这个算法流程是什么样的，小编开了两个一维数组分别叫f和s。那么它们是干啥的呢？f[i]就表示以i为根的最长链，s[i]表示以i为根的次长链，你肯定要问什么是最长链？什么是次长链？先看下面的图：

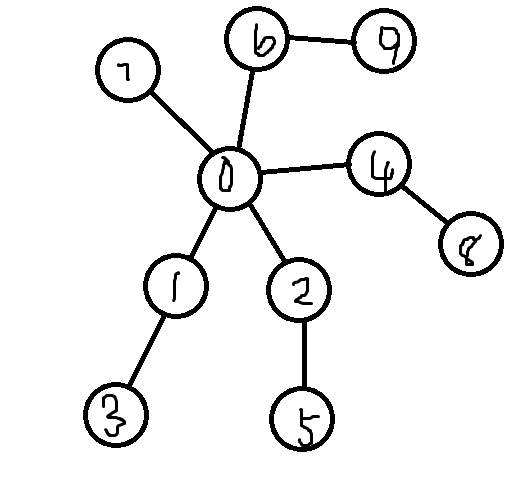
　　忽略小编拙劣的画技，比如说1是当前的根节点，那么节点1和3就组成了一棵树，如3 -> 1 -> 0 -> 4 -> 8这条链中1 -> 3就是次长链，1 -> 0 -> 4 -> 8就是最长链，也就是说树中的一点像外延伸，可以有至多两个方向，一个方向长（最长链），一个方向短（次长链）。如果一样长就无所谓了。

　　了解了小编口中的最长链和次长链后，那么就来构思搜索，那么我们改放些什么参数呢？存放下当前节点u和父节点fa（上次的节点），为了干啥呢？u的延伸方向有两个，要找一个当子节点v，可别返回去把父节点当了子节点。那么在回溯过程中考虑：会有这样的情况发生：f[v]+1>f[u]，那么此时说明u的最长链可以通过子节点更新，层层回溯，最长链数组f就会赋上初值。那么那么次长链s呢？在f更新的时候可以把先前f的值给s，如果f没有被更新过，那么s就是0，如果更新过，那么就一定是在其它子树中更新的，s就更新成了，子树外侧的链的长度。当上述情况不发生，而却f[v]+1>s[u]时，那么就可以更新s的值，有s[u]=f[v]+1的式子，这说明最长链已经被更新过（否则f[u]=0，一定会发生第一种情况），并且在其它子树上，所以当前子树就是次长链的一端，直接更新就好了。

　　但是，这还不完全对，还会出现这样的现象：①较长链的长度比最长链还长，②最长链和较长链的长度更新还不完全；因此，我们就有必要尽行第二轮的搜索，没错还要再搜一次，而第二次的重心就放在了更新树外距离上，顺便解决上述两个问题。与第一次搜索不同的是，这次搜索加入了一个新的参数：当前节点的树外最远距离dis。那么在树外会出现这样的情况：f[v]+1==f[u]，很明显，这是第一次搜索时的操作，这样判断反而能告诉我们是否当前节点在u的最长链上，那么下一次的dis就要在dis+1和s[u]+1中选一个，因为在上一轮搜索中很多s已经更新过了，可以直接用，如果没有就用dis+1另起炉灶吧。同样，如果f[v]+1！=f[u]，那么就在dis+1和f[u]+1选一个。

　　这样两次搜索之后就很清晰明了了。只要在所有总链长（即最长链f[i]+次长链s[i]）中找出最长的，那么再遍历一遍把所有等于最长总链长的i输出就可以了。

　　最后，请注意一点：数据规模高达2*10⁵，一定不能用二维数组，要用邻接表或其他（小编使用的是vector动态数组）。

　　代码如下：

 1 #include<iostream>
 2 #include<vector>
 3 using namespace std;
 4 vector<int>road[1000000];
 5 int n,a,b,maxn,f[1000000],s[1000000];
 6 void dfs1(int u,int fa)
 7 {
 8     for(int i=0;i<(int)road[u].size();i++)
 9     {
10         int v=road[u][i];
11         if(v==fa) continue;//子节点也连着父节点，不能往回走 
12         dfs1(v,u);
13         if(f[v]+1>f[u]) //更新 
14         {
15             s[u]=f[u];//把最长链先给次长链 
16             f[u]=f[v]+1;
17         }
18         else if(f[v]+1>s[u]) s[u]=f[v]+1;
19     }
20 }
21 void dfs2(int u,int fa,int dis)//dis是子树外侧的链长 
22 {
23     for(int i=0;i<(int)road[u].size();i++)
24     {
25         int v=road[u][i];
26         if(v==fa) continue;
27         if(f[v]+1==f[u]) dfs2(v,u,max(dis+1,s[u]+1));//在最长链上 
28         else dfs2(v,u,max(dis+1,f[u]+1));//在次长链上 
29     }
30     if(dis>f[u])//更新第一次搜索后的结果 
31     {
32         s[u]=f[u];
33         f[u]=dis;
34     }
35     else if(dis>s[u]) s[u]=dis;
36 }
37 int main()
38 {
39     cin>>n;
40     for(int i=1;i<=n-1;i++)
41     {
42         cin>>a>>b;
43         road[a].push_back(b);
44         road[b].push_back(a);//路是双向的 
45     }
46     dfs1(0,0);//第一次搜索 
47     dfs2(0,0,0);//第二次搜索 
48     for(int i=0;i<n;i++)
49     maxn=max(maxn,f[i]+s[i]);//最大总链长 
50     for(int i=0;i<n;i++)
51     {
52         if(s[i]+f[i]==maxn)
53         cout<<i<<endl;
54     }
55     return 0;
56 }

　　这道题很不容易理解，如果真的想搞明白，那么可以使用调试，网上博客稀少，却只有几个字加代码。小编全靠调试理解的，调试是个好东西。

　　希望数位动态规划没有这么变态。

posted @ 2019-07-14 19:33 c1714-gzr 阅读(609) 评论(0) 编辑收藏举报

刷新页面返回顶部