【披着递推皮的动态规划】 山区建小学 题解

　　今天小编随意写了一道老师布置的题，这是一道看起来很普通的题，我却不明白它为什么放在递推中……

　　废话不多说，直接看题。

▍1197：山区建小学

【题目描述】

政府在某山区修建了一条道路，恰好穿越总共m个村庄的每个村庄一次，没有回路或交叉，任意两个村庄只能通过这条路来往。已知任意两个相邻的村庄之间的距离为di(为正整数)，其中，0<i<m。为了提高山区的文化素质，政府又决定从m个村中选择n个村建小学(设0<n≤m<500)。请根据给定的m、n以及所有相邻村庄的距离，选择在哪些村庄建小学，才使得所有村到最近小学的距离总和最小，计算最小值。

【输入】

第1行为m和n，其间用空格间隔

第2行为m−1 个整数，依次表示从一端到另一端的相邻村庄的距离，整数之间以空格间隔。

例如:

 

10 3
2 4 6 5 2 4 3 1 3

 

表示在10个村庄建3所学校。第1个村庄与第2个村庄距离为2，第2个村庄与第3个村庄距离为4，第3个村庄与第4个村庄距离为6，...，第9个村庄到第10个村庄的距离为3。

 

【输出】

各村庄到最近学校的距离之和的最小值。

【输入样例】

10 2
3 1 3 1 1 1 1 1 3

【输出样例】

18

【来源】

No

 

▍题目分析

　　这道题乍一看，似乎没有什么思路，那么就先返璞归真，先想想怎么打暴力求解这道题吧。在m个村庄中要建立n个小学，先不考虑时间复杂度，那么我们可以先当成m中取n个的时间复杂度求出所有情况，再进行暴力算出每一种情况的距离和，再比较出最小的，在只会用递推时，我们似乎就只能这么去做，但是这种暴力的方法显然是很慢的，过题几乎不可能，那么在这种想法的基础上，加入动态规划的思想，问题将会迎刃而解。

　　那么先想想动态规划的本质和作用，动态规划只是一种思想，并不是一种写法，它的本质就是降低问题的规模（说白了就是经过优化之后的暴力算法），在节约问题的规模的同时除去冗余计算以节约时间。但是这道题很不好想，也很难和动态规划联系起来，还涉及到区间dp，状态转移方程也是一大难点（小编也琢磨了半天）。为了大家的理解方便（理解万岁！），那么就分模块讲解。

　　动态规划的一般步骤包括确定子问题、设计状态、写出状态转移方程、确定边界条件、确定实现方式、确定优化方法（似乎本题不需要），那么就逐一思考。

　　　确定子问题：这道题的子问题没有那么麻烦，直接一想就出来了，比如说现在的问题是m个村庄中选n个建小学，那么我们可以考虑在前m个村庄中选n-1个的情况，可以考虑在前m个村庄中选n-2个的情况，也可以考虑在前m-1个村庄中选n-1个的情况，……这些都是原问题的子问题。

　　　设计状态：按照刚才所划分的子问题，我们可以自然的想到状态是什么，定义数组f[ i ][ j ]为当在前i个村庄中建立j个小学的最小路程和，那么原问题（在m个村庄中选n个建小学）的答案就是f[ m ][ n ]，这样问题就涉及好了。

　　　状态转移方程：写这个状态转移方橙方程，是比较难的，首先假装我们已经算出了每两个村庄之间建立一个小学的最短距离和，并把这些数据存在数组c[ i ][ j ]，那么我们就知道了村庄i到村庄j这个区间内建一个小学的最短距离和，先不要考虑我们是怎么算出来的；

----------------------------------------------------------------------------------------------------------------------------------------

　　　举个栗子：比如现在有5个村庄，现在我们正要通过动态规划更新f[ 3 ][ 2 ]的值，先画个草图：

　　　

　　因为我们只需要选2个，那么我们为了达到目的更新f[ 3 ][ 2 ]的值，我们会不择手段，就算再来一层循环也在所不惜（情况需要），再来一层循环那么我们就从1到3遍历前三个村庄，那么我们会不停枚举每一个村庄为边界（也就是说这个村庄及所有它左边的村庄最近的小学在它的左边，而右边的所有村庄都不会去左边的小学去上学，因为已经有更近的了）的情况，找到一个最小值，然后更新f[ 3 ][ 2 ]，详见图示：

　　

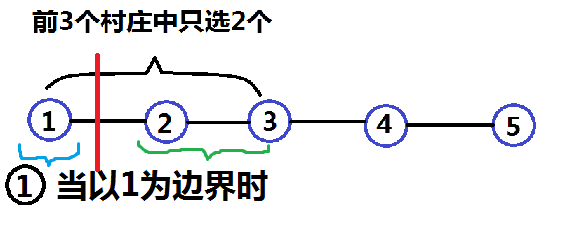
　　此时三个村庄被划分成了两部分，当只有2个村庄建小学时，这就意味着蓝色部分建2-1个小学，也就是前1个村庄中建1所小学（即f[ 1 ][ 1 ]）；而在绿色部分只建1所小学，也就是村庄2和村庄3内建1个小学的最短距离和，即c[ 2 ][ 3 ]；当然，将蓝色部分最短距离和和绿色部分最短距离和加起来，就是f[ 3 ][ 2 ]的值啦，但这还不一定是最小的，所以还有考虑以2，3为边界时的值，选一个最小的。如果到此还是不理解，可以停下来利用画图工具来接着模拟以2，3为边界的情况。

----------------------------------------------------------------------------------------------------------------------------------------

　　类比以上的栗子，如果用i，j，k来表示当以k为边界时前i个村庄选j个建小学（即以k为边界时的f[ i ][ j ]值），那么状态转移方程则可以表述为f[ i ][ j ]=min( f[ i ][ j ],f[ k ][ j-1 ]+c[ k+1 ][ i ] );也就是所有f[ k ][ j-1 ]+c[ k+1 ][ i ] 中最小的那个。我感觉表达的还行吧，如果不理解一定要画图。　　

　　　确定边界条件：这个似乎没有什么问题吧，一直更新到f [ m ][ n ]就可以了，然后输出它的值；初始赋值的式子为f[i][1]=c[1][i];，这个很容易理解吧，无论如何前i个村庄中建一个小学时，都等于1到第i个村庄只建一个学校的最短距离和，这不正是我们上文中所假装求出的吗？只要i from 1 to m赋f的初值就可以了。

　　　确定实现形式：动态规划的实现形式主要就两种：记忆化搜索和数组递推，这里使用数组递推的形式。

　　　确定优化方法：貌似没有。

　　

 ▍实现方法

 

　　　Part one

　　我们分开来写这道题，先写简单的，定义一大堆变量，变量作用，见上文。

　　 int m,n,a[1000][1000],c[1000][1000],f[1000][1000]; 

　　最好在main函数外边定义，那样初值就全是0了。

 

　　　Part two

　　很平凡而没有技术含量的输入……

　　 cin>>m>>n; 2 for(int i=1;i<m;i++) 3 cin>>a[i][i+1]; 

 

　　　Part three

　　还记得吗？我们当初假装我们已经知道了每两个村庄之间建立一个小学的最短距离和，而我们现在就要面临怎么真正算出来这个问题了，为了算出每两个村庄之间建立一个小学的最短距离和，那么我们首先要知道这两个村庄的距离吧，求距离代码如下：

　　

for(int i=1;i<=m;i++)
    for(int j=i+1;j<=m;j++)
    a[i][j]=a[j][i]=a[i][j-1]+a[j-1][j];

　　它这个算法和floyed很像，在学这之前，希望身为大牛的您先学会floyed，这样理解就很方便了。核心思路就是使原来未知距离的i，j两点通过j-1这个点来过渡刷新距离的值，如果画画图，举个栗子，就很清晰明了了。

 

　　　Part four

　　算出了距离，那么我们就可以开始算我们假装知道的距离和了。举个栗子，比方说要在3~6这个区间内建一所小学，那么你会选几号村庄呢？当然是选中间的！（3+6）/2=4，所以建在4号村庄，这是为什么呢？先假设在3号村庄建，那么将如下图所示：

　　

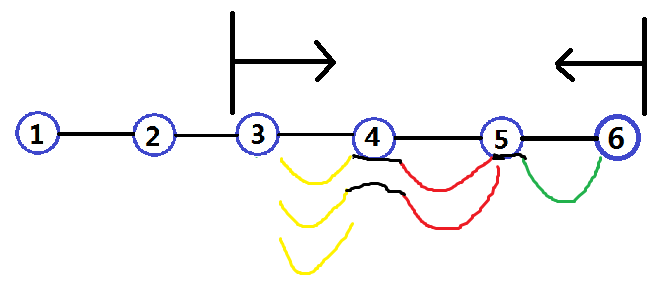
　　因为4，5，6都去3号村庄上学，所以总路程将会是3*黄+2*红+1*绿。但是如果4号村庄建小学呢？

　　

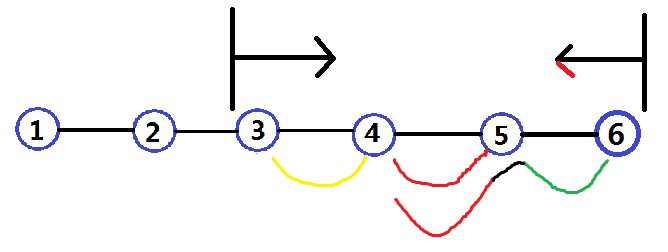
　　因为3，5，6都去4号村庄上学，所以总路程将会是1*黄+2*红+1*绿。相比来说少走了一段距离，接着5，6号村庄建小学也以此类推，同时会发现由于区间内一共有偶数个村庄，所以4，5都在中间，且距离和一样，所以两者均可。

　　那么这样我们就明确了怎么知道哪一个村庄该建小学，然后就能求出每两个村庄之间建立一个小学的最短距离和了。代码如下：

　　

for(int i=1;i<=m;i++)
    for(int j=i+1;j<=m;j++)
    {
        int mid=(i+j)/2;
        for(int k=i;k<=j;k++)
        c[i][j]+=a[k][mid];
    }

 

　　　Part five

　　那么现在就要正儿八经开始动态规划了，先得赋初始值了吧……

　　 for(int i=1;i<=m;i++) 2 f[i][1]=c[1][i]; 

 

　　　Part six

　　利用之前得到的状态转移方程，通过数组递推一步一步得到结果，代码如下：

　　

for(int i=1;i<=m;i++)
    for(int j=2;j<=n;j++)
    {
        f[i][j]=999999;
        for(int k=j-1;k<=i;k++)
        {
            f[i][j]=min(f[i][j],f[k][j-1]+c[k+1][i]);
        }
    }

 

　　　Part seven

　　输出结果……

　　 cout<<f[m][n]; 

　　

　　对，这道题做到这里就完了，这道题还是很不好理解的，需要多看，小编在写博客的时候也多次犯蒙。

▍Code speaks louder than word!

 　　代码胜于雄辩，总结好的代码如下：

　　

#include<iostream>
#include<cmath>
using namespace std;
int m,n,a[1000][1000],c[1000][1000],f[1000][1000];
int main()
{
    cin>>m>>n;
    for(int i=1;i<m;i++)
    cin>>a[i][i+1];
    
    
    for(int i=1;i<=m;i++)
    for(int j=i+1;j<=m;j++)
    a[i][j]=a[j][i]=a[i][j-1]+a[j-1][j];
    
    
    for(int i=1;i<=m;i++)
    for(int j=i+1;j<=m;j++)
    {
        int mid=(i+j)/2;
        for(int k=i;k<=j;k++)
        c[i][j]+=a[k][mid];
    }
    
    
    for(int i=1;i<=m;i++)
    f[i][1]=c[1][i];
    
    
    for(int i=1;i<=m;i++)
    for(int j=2;j<=n;j++)
    {
        f[i][j]=999999;
        for(int k=j-1;k<=i;k++)
        {
            f[i][j]=min(f[i][j],f[k][j-1]+c[k+1][i]);
        }
    }
    
    
    cout<<f[m][n];
    return 0;
}