树—红黑树基础集合
红黑树是什么?要说到红黑树,就不得不说二叉排序树(Binary Sort Tree,又称二叉查找树或二叉搜索树)。
一、二叉排序树(二叉查找树)
二叉排序树都满足下列性质:
(1)若左子树不空,则左子树上所有结点的值均小于或等于它的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
(3)左、右子树也分别为二叉排序树;
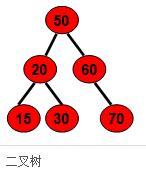
既然有这种树,那一定有它的作用,二叉排序树正如其名,可以用来排序,利用以上的三个性质,可以通过二分来快速查找。
举个栗子:以上图为例,假设要查找值30的节点。
1.从根节点开始查看,30<50;
2.利用性质查找根结点的左孩子,30>20;
3.查找其右孩子,30=30,找到了所求的节点;
听起来很棒的样子,查找一个值变得更快,似乎时间复杂度并不高,最大查找次数=树的深度。可它有没有不足的地方?
当然有!!!
please看下面的图:
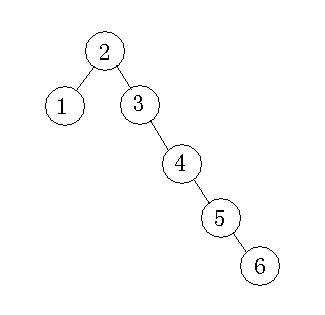
正所谓,凡事都有利弊,很明显,二叉排序树的查找次数和它的深度息息相关,简直是中毒太深。
看了上图作何感想?这张图上的二叉树好端端变成了近似一根线的树,看起来怪怪的,这样查找并没有达到预期效果,查找一个数时,就只能一条路走到黑,这是二叉排序树的一种很糟糕的情况(最坏递归到叶子节点,叶子节点最坏情况即为树的深度),这是二叉树的一种不平衡状态,因此我们希望这棵树能够高度平衡,如何改变这种不平衡状态?对二叉树进行改进,使得动态操作下,每种种操作的最坏情况、期望或平摊的时间复杂度为O(logn),这样的二叉查找树称为平衡树。此时,主角红黑树就派上用场了。
二、红黑树
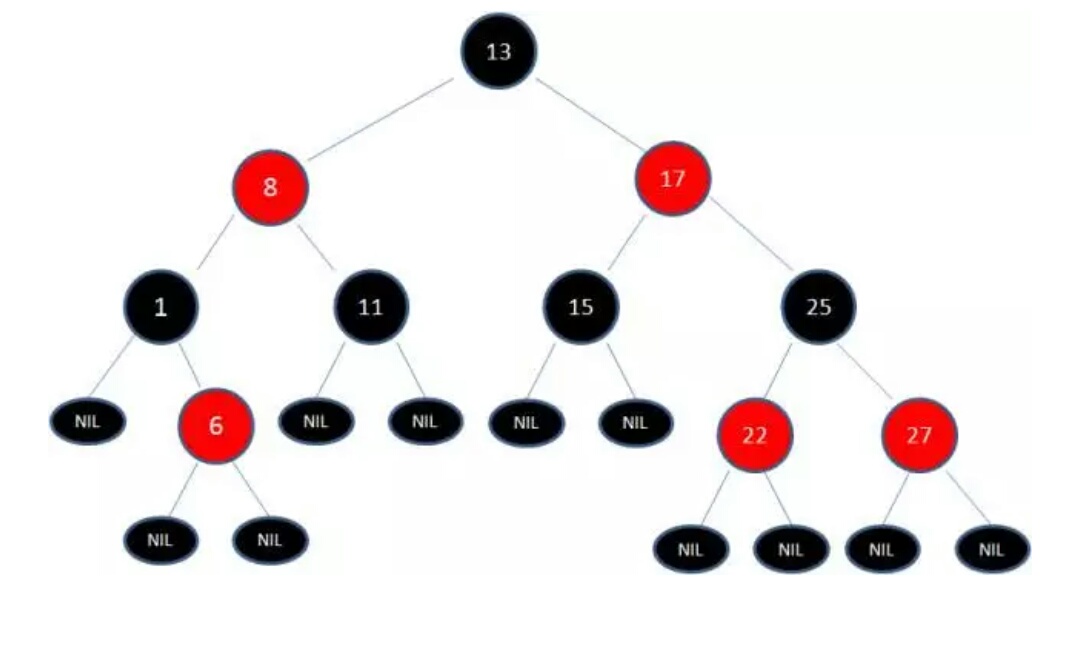
红黑树的性质:
1.节点是红色或黑色。
2.根节点是黑色。
3.每个叶子节点都是黑色的空节点(NIL节点)。
4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
看了以上性质应该都会认为红黑比较繁琐,但是这些性质约束了红黑树: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。所以是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。
红黑树的操作:
在红黑树上只读操作不需要对用于二叉查找树的操作做出修改,因为它也是二叉查找树。但是,在插入和删除之后,红黑属性可能变得违规。恢复红黑属性需要少量(O(log n))的颜色变更(这在实践中是非常快速的)并且不超过三次树旋转(对于插入是两次)。这允许插入和删除保持为 O(log n) 次,但是它导致了非常复杂的操作。翻译成人话来说就是红黑树操作时会变色。
1)插入节点和删除节点
在讨论红黑树的插入操作之前必须要明白,任何一个即将插入的新结点的初始颜色都为红色。这一点很容易理解,因为插入黑点会增加某条路径上黑结点的数目,从而导致整棵树高度的不平衡。但如果新结点父结点为红色时(如图2所示),将会违返红黑树性质:一条路径上不能出现相邻的两个红色结点。这时就需要通过一系列操作来使红黑树保持平衡。
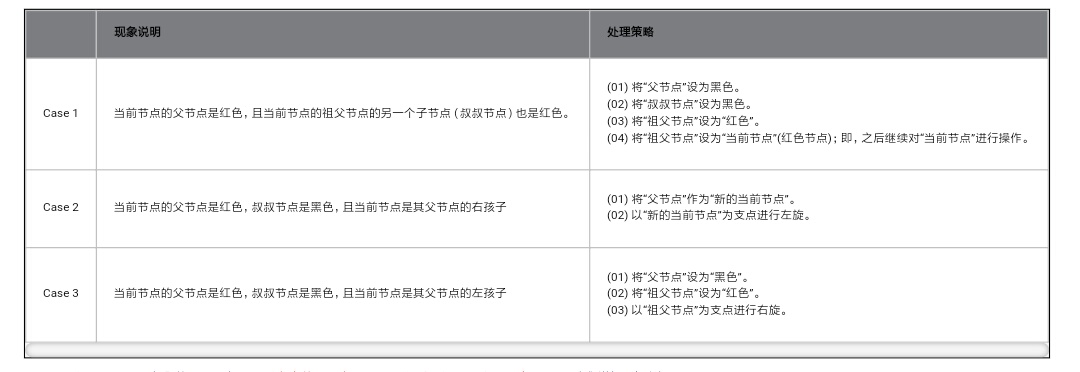
//一张较全面的图
如何插入和删除?小编最近看了一篇博客,图又多又好,推荐看一看,能力有限,不做过多解释。(其实因为手太懒) https://blog.csdn.net/eric491179912/article/details/6179908
2)旋转
红黑树的旋转操作和AVL树一样,分为LL、RR、LR、RL四种旋转类型,差别在于旋转完成后改变的是结点的颜色,而不是平衡因子。旋转动画演示请参考AVL这篇文章中的Flash动画:推荐文章 http://www.cnblogs.com/abatei/archive/2008/11/17/1335031.html (转);
感谢看到末尾的同志们,你们的鼓励将化作小编前进的动力!![]()


