CF708C Centroids 题解
题意分析
给出一棵树,求有多少个节点满足在树上删去一条边再加入一条边后可以成为树的重心。
思路分析
设当前节点为 $x$ 。经过分析后很容易发现,题目中要求的操作一定是在以当前节点为根时,将其中一棵子树接到根节点上,设这棵子树的根节点为 $p_x$。则若 $x$ 已经是重心,则不用操作;若 $x$ 不是重心,则有且只有一棵 $x$ 的直接子树(即以 $x$ 的儿子节点为根的子树)的大小 $>\left \lfloor \frac{n}{2}\right \rfloor$,因此一定要把这棵直接子树中的一棵子树接到 $x$ 上。显然,这棵被移动的子树应该是这棵直接子树中的最大的大小不超过 $\frac{n}{2}$ 的子树。可以证明这个移动策略一定是最优的。然后判断移动后 $x$ 是否为重心即可。
对于每个节点都重新计算显然复杂度太高,发现很多信息可以重复利用,考虑换根。对于一个普通节点 $x$ , $p_x$ 可能位于以 $x$ 为根的子树当中,也有可能不位于。对这两种情况,可以分两路进行递推。
1. $p_x$ 在以 $x$ 为根的子树当中
找到 $x$ 的最大直接子树,若该子树的大小 $>\left \lfloor \frac{n}{2}\right \rfloor$ ,那么就从这棵子树中找出最大的不超过 $\frac{n}{2}$ 的子树,这棵子树的根节点即为 $p_x$ 。若没有,说明 $p_x$ 不在这或者 $x$ 原本就是重心。
2. $p_x$ 不在以 $x$ 为根的子树当中
有两种情况:
- $p_x$ 在以 $x$ 的父亲为根的子树当中
这种情况下,可以通过记录每个节点的最大的满足大小 $\leq\left \lfloor \frac{n}{2}\right \rfloor$ 的子树。注意,如果 $x$ 恰好在该子树当中,则需要选择第二大的合法子树,因此需要存储最大的和第二大的两个信息。
- $p_x$ 不在以 $x$ 的父亲为根的子树当中
这种情况下,直接将整棵树去掉以 $x$ 的父亲为根的部分看作一个子树,用类似于“ $p_x$ 在以 $x$ 为根的子树当中”的方法去处理即可。
具体实现
根据上面的分析,需要对于每个节点,需要存储以下信息:
- $son_{x,0},son_{x,1}$ 分别存储以 $x$ 为根的子树中最大的和次大的大小 $\leq\left \lfloor \frac{n}{2}\right \rfloor$ 的子树的大小;
- $fa_x$ 存储整棵树除去以 $x$ 为根的子树外最大的大小 $\leq\left \lfloor \frac{n}{2}\right \rfloor$ 的子树的大小;
- $siz_x$ 存储以 $x$ 为根的子树的大小;
- $ansp_x$ 存储 $p_x$;
- $maxson_x$ 存储 $x$ 的重儿子,即子树最大的儿子;
- $ans_x$ 存储 $x$ 的答案。
1. 预处理
预处理出 $siz,maxson,son,ansp$ 四个数组的值。前两个数组的处理很简单,就不赘述了; $son$ 数组,对于当前扫描到的子节点,若以该子节点为根的子树大小 $\leq\left \lfloor \frac{n}{2}\right \rfloor$ ,则用其更新 $son$ 数组,否则用该子节点的 $son_0$ 进行更新。处理 $son$ 数组时,若决策更优,则更新 $ansp$ 数组。
void check(int x,int y,int p)
{
if(y>son[x][0] && y<=n/2)//与最大的比较
son[x][1]=son[x][0],son[x][0]=y,ansp[x]=p;
else
if(y>son[x][1] && y<=n/2)//比最大的小,则与次大的比较
son[x][1]=y;
}//判断决策是否更优
void pre(int x,int f)
{
siz[x]=1;
for(int i=head[x];i;i=Next[i])
{
int y=ver[i];
if(y==f)
continue;
pre(y,x);
siz[x]+=siz[y];
if(siz[y]>siz[maxson[x]])
maxson[x]=y;//找重儿子
check(x,siz[y]<=n/2?siz[y]:son[y][0],y);//注意不能让同一子节点贡献两个决策
}
}
2. 处理 $fa$ 同时求解
用类似于处理 $son$ 数组的方法处理 $fa$ 数组,这里就不赘述了。然后分别判断父节点方向和子树方向的两种情况是否合法,以及其本身是否就是重心,从而求解。
void checkfa(int x,int y)
{
if(y>fa[x] && y<=n/2)
fa[x]=y;
}//判断决策是否更优
void solve(int x,int f)
{
checkfa(x,n-siz[f]<=n/2?n-siz[f]:fa[f]);
if(ansp[f]==x)//本身在最大子树,则采用次大作为决策
checkfa(x,son[f][1]);
else//否则采用最大
checkfa(x,son[f][0]);
if(siz[maxson[x]]>n/2)//在子树内
ans[x]=(siz[maxson[x]]-son[maxson[x]][0]<=n/2);
else
if(n-siz[x]>n/2)//在父节点方向
ans[x]=(n-siz[x]-fa[x]<=n/2);
else
ans[x]=1;//原本就是重心
for(int i=head[x];i;i=Next[i])
{
int y=ver[i];
if(y==f)
continue;
solve(y,x);
}
}
图例解释
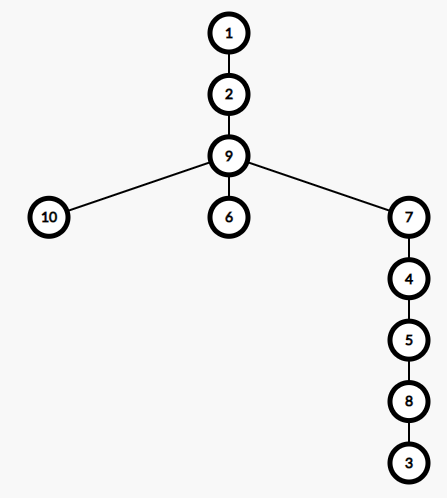
以上图为例(默认节点 $1$ 作为根节点):(为了方便,以下的最大子树均指 $\leq\left \lfloor \frac{n}{2}\right \rfloor$ 的子树)
- 最大子树位于子树方向且为直接子树:9
- 最大子树位于子树方向且不为直接子树:1、2、6、10
- 最大子树位于父亲方向且为直接子树:7
- 最大子树位于父亲方向且不为直接子树:3、4、5、8
#include<iostream>
#include<cstdio>
using namespace std;
const int N=1e6+100;
int n,tot;
int head[N],ver[2*N],Next[2*N];
int siz[N],ans[N],ansp[N],maxson[N],fa[N],son[N][2];
void add(int x,int y)
{
ver[++tot]=y,Next[tot]=head[x],head[x]=tot;
ver[++tot]=x,Next[tot]=head[y],head[y]=tot;
}//邻接表
void check(int x,int y,int p)
{
if(y>son[x][0] && y<=n/2)
son[x][1]=son[x][0],son[x][0]=y,ansp[x]=p;
else
if(y>son[x][1] && y<=n/2)
son[x][1]=y;
}//子树方向更新
void checkfa(int x,int y)
{
if(y>fa[x] && y<=n/2)
fa[x]=y;
}//父亲方向更新
void pre(int x,int f)
{
siz[x]=1;
for(int i=head[x];i;i=Next[i])
{
int y=ver[i];
if(y==f)
continue;
pre(y,x);
siz[x]+=siz[y];
if(siz[y]>siz[maxson[x]])
maxson[x]=y;
check(x,siz[y]<=n/2?siz[y]:son[y][0],y);
}
}//预处理
void solve(int x,int f)
{
checkfa(x,n-siz[f]<=n/2?n-siz[f]:fa[f]);
if(ansp[f]==x)
checkfa(x,son[f][1]);
else
checkfa(x,son[f][0]);
if(siz[maxson[x]]>n/2)
ans[x]=(siz[maxson[x]]-son[maxson[x]][0]<=n/2);
else
if(n-siz[x]>n/2)
ans[x]=(n-siz[x]-fa[x]<=n/2);
else
ans[x]=1;
for(int i=head[x];i;i=Next[i])
{
int y=ver[i];
if(y==f)
continue;
solve(y,x);
}
}//处理 fa 同时求解
int main()
{
scanf("%d",&n);
for(int i=1,x,y;i<n;i++)
{
scanf("%d%d",&x,&y);
add(x,y);
}
pre(1,0),solve(1,0);
for(int i=1;i<=n;i++)
printf("%d ",ans[i]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号