LCA详解
LCA,即最近公共祖先,在图论中应用比较广泛。
LCA的定义如下:给定一个有根树,若节点$z$同时是节点$x$和节点$y$的祖先,则称$z$是$x,y$的公共祖先;在$x,y$的所有公共祖先当中深度最大的称为$x,y$的最近公共祖先。下面给出三个最近公共祖先的例子:
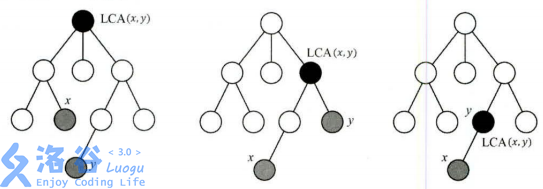
显然,从上面的例子可以得出,$LCA(x,y)$即为$x,y$到根节点的路径的交汇点,也是$x$到$y$的路径上深度最小的节点。
求LCA的方法通常有三种:
当然,求LCA还有其它方法,例如树剖等,请读者自行了解,本文主要讲解上面提到的三种方法。
向上标记法是求LCA最直接的方法,直接根据定义来求,单次查询的时间复杂度最坏为$O(n)$(看起来好像还挺快的,不过什么题会只有一次查询呢)
算法流程:
- 从x节点向上一直走到根节点,沿途标记经过的节点
- 从y节点向上一直走到根节点,当第一次遇到已标记的节点时,该节点就是$LCA(x,y)$
该方法思想是绝对简单的,实现也简单,因此在这里就不给出具体实现了。不过由于其时间复杂度过高,在实际中基本不会应用到,在这里提一下主要还是为讲解Tarjan算法做基础。
树上倍增法应用非常广泛,读者可以深入地学习。用树上倍增法求LCA的时间复杂度为$O((n+m)logn)$。
树上倍增法用到了二进制拆分的思想。在求LCA时,用$f_{i,j}$存储$i$的第$2^j$辈祖先的节点编号,特别地,若该节点不存在,则将值定为0。根据这个定义,可以推出以下的递推式:
f[i][j]=f[f[i][j-1]][j-1];
这个递推式很好得出,请读者根据定义自己思考。
那么怎样对$f$数组进行递推呢?根据递推式可以发现,一个节点的$f$数组的值要通过它的祖先节点转移过来,因此我们在递推时要采用从根到叶子的遍历。普遍使用的方法有dfs和bfs,在这里我们用bfs来实现。
由于接下来的步骤还需要关系到节点的深度,因此我们定义一个数组$d_i$存储$i$节点的深度,在递推$f$数组的同时递推出来。$d$数组的递推式更简单了,就不多说了吧。
步骤:
- 建立一个空队列,并将根节点入队,同时存储根节点的深度
- 取出队头,遍历其所有出边。由于存储的时候是按照无向图存储,因此要进行深度判定,对于连接到它父亲节点的边,直接continue即可。记当前路径的另一端节点为$y$,处理出$y$的$d$、$f$两个数组的值,然后将$y$入队。
- 重复第2步,直到队列为空
以上部分是树上倍增法的预处理,也是比较通用的对于树上倍增的预处理,时间复杂度$O(nlogn)$。接下来是求LCA的核心部分。
步骤:
- 设查询的两个节点分别为$x,y$,令$d_x\leq d_y$(即,若$d_x>d_y$,则交换$x,y$)。
- 利用二进制拆分的思想,将$y$上移到与$x$相同的深度。具体来说,就是令$y$依次尝试向上走$2^{logn},...,2^1,2^0$步,并且使$y$的深度不低于$x$。
- 若此时$x==y$,则说明当前节点为$LCA(x,y)$,也就是文章开头给出的图中的第三种情况。此时直接输出即可。
- 再次利用二进制拆分的思想,将$x,y$同时上移并保持$x!=y$。
- 完成第4步后,此时$x$和$y$一定在某个节点的两个子节点上,因此它们的父亲节点就是$LCA(x,y)$。因为一个节点利用二进制拆分进行移动可以到达它的任意一个祖先节点,而在第4步中保持$x!=y$,也就是将$x,y$移动到了它们共同的祖先节点以下的最浅的节点,也就是该节点的某个子节点中。所以,此时$x,y$的父亲节点就是$LCA(x,y)$。
树上倍增法代码:
#include<iostream>
#include<cstdio>
#include<queue>
#include<cmath>
using namespace std;
const int N=6e5;
int n,m,s,t,tot=0,f[N][20],d[N],ver[2*N],Next[2*N],head[N];
queue<int> q;
void add(int x,int y)
{
ver[++tot]=y,Next[tot]=head[x],head[x]=tot;
}//邻接表存边操作。由于只求LCA时不关心边权,因此可以不存边权
void bfs()
{
q.push(s);
d[s]=1;//将根节点入队并标记
while(q.size())
{
int x=q.front();q.pop();//取出队头
for(int i=head[x];i;i=Next[i])
{
int y=ver[i];
if(d[y])
continue;
d[y]=d[x]+1;
f[y][0]=x;//初始化,因为y的父亲节点就是x
for(int j=1;j<=t;j++)
f[y][j]=f[f[y][j-1]][j-1];//递推f数组
q.push(y);
}
}
}
int lca(int x,int y)
{
if(d[x]>d[y])
swap(x,y);
for(int i=t;i>=0;i--)
if(d[f[y][i]]>=d[x])
y=f[y][i];//尝试上移y
if(x==y)
return x;//若相同说明找到了LCA
for(int i=t;i>=0;i--)
if(f[x][i]!=f[y][i])
{
x=f[x][i],y=f[y][i];
}//尝试上移x、y并保持它们不相遇
return f[x][0];//当前节点的父节点即为LCA
}
int main()
{
cin>>n>>m>>s;
t=log2(n)+1;
for(int i=1;i<n;i++)
{
int x,y;
scanf("%d%d",&x,&y);
add(x,y),add(y,x);
}
bfs();
while(m--)
{
int a,b;
scanf("%d%d",&a,&b);
printf("%d\n",lca(a,b));
}
return 0;
}
对于树上倍增法还有一些应用,这里给出一道比较不错的树上倍增法的应用题:
读者可以先尝试解题,实在解不出来再借鉴题解的思路。
Tarjan牛逼!
Tarjan算法求LCA的本质是用并查集对向上标记法进行优化,是一种离线算法,时间复杂度$O(n+m)$。
对于并查集的基本操作,不了解的可以点击食用。
求LCA的Tarjan算法主体由dfs实现,并用并查集进行优化。对于每个节点,我们增加一个标记:
- 若该节点没有访问过,则初值为0
- 若该节点已访问但还没有回溯,则标记为1
- 若该节点已访问且已回溯,则标记为2
显然,对于当前访问的节点$x$,它到根节点的路径一定都被标记为1。因此对于任意一个与$x$相关的询问,设询问的另一个节点为$y$,则$LCA(x,y)$即为$y$到根节点的路径中第一个,也就是最深的标记为1的节点。
求这个节点的方法可以用并查集优化。当一个节点的标记改为2的同时,将它合并到其父节点的集合当中。显然,此时它的父节点的标记一定为1,并且单独构成一个集合,因为这个父节点还没有进行过回溯操作。
在合并过后,遍历关于当前节点$x$的所有询问,对于任意一个询问,若$y$的标记为2,说明其已经被访问过,并且它的并查集指向的那个节点,也就是$y$到根节点的路径中最深的还没有回溯的节点,一定就是$LCA(x,y)$。
对于询问,我们可以用一个不定长数组存储与每个节点相关的询问,并且每个询问用一个二元组表示,第一维存储该询问的另一个节点,第二维存储该询问输入的次序,以便按顺序输出
这样,Tarjan算法求LCA的步骤就很明了了:
- 从根节点开始进行dfs
- 将当前节点标记为1
- 遍历当前节点的所有出边;若当前边的终点还没有访问过,则访问它,访问过后将该节点合并到当前节点的集合中;
- 遍历与当前节点相关的所有询问;若当前询问的另一个节点的标记为2,则该询问的答案即为另一个节点所在集合的代表元素
- 将当前节点标记为2
思路清晰之后,实现起来不会很难
Tarjan算法代码:
#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int N=6e5;
int n,m,s,tot=0,fa[N],v[N],ans[N],ver[2*N],Next[2*N],head[N];
vector< pair<int,int> > query[N];
void add(int x,int y)
{
ver[++tot]=y,Next[tot]=head[x],head[x]=tot;
}//邻接表插入操作
int get(int a)
{
return fa[a]==a?a:fa[a]=get(fa[a]);
}//并查集查找操作
void add_query(int x,int y,int id)
{
query[x].push_back(make_pair(y,id));
query[y].push_back(make_pair(x,id));
}//添加询问
void tarjan(int x)
{
v[x]=1;
for(int i=head[x];i;i=Next[i])
{
int y=ver[i];
if(v[y])
continue;//若访问过则不再访问
tarjan(y);
fa[y]=x;//将子节点合并到自己的集合中
}//遍历所有出边
for(int i=0;i<query[x].size();i++)
{
int y=query[x][i].first,id=query[x][i].second;
if(v[y]==2)
ans[id]=get(y);
}//遍历所有相关的询问
v[x]=2;
}
int main()
{
cin>>n>>m>>s;
for(int i=1;i<=n;i++)
fa[i]=i;
for(int i=1;i<n;i++)
{
int x,y;
scanf("%d%d",&x,&y);
add(x,y),add(y,x);
}
for(int i=1;i<=m;i++)
{
int a,b;
scanf("%d%d",&a,&b);
if(a==b)
ans[i]=0;//特判,若两个节点相等直接输出
else
add_query(a,b,i);
}
tarjan(s);
for(int i=1;i<=m;i++)
printf("%d\n",ans[i]);
return 0;
}
习题:
声明:本文部分内容参考lyd的蓝书。
2019.5.14 于厦门外国语学校石狮分校


 浙公网安备 33010602011771号
浙公网安备 33010602011771号