第二类斯特林数

第二类斯特林数总结

1. 定义

第二类斯特林数S(n,m)表示的是把n个不同的小球放在m个相同的盒子里方案数。
ps:为了看得清楚，有时候我们也用{n，m}来表示S(n,m)。

2. 求法

两种：

• 递推法：

\(S(n,m)=S(n−1,m−1)+m*S(n−1,m)\)
即讨论第一个球是否单独在一个盒子里面。单独：S(n−1,m−1)，不单独：m*S(n−1,m)
（如果不独占一盒，那么把这个球放进任一个盒子，这个盒子就相当于与其他的盒子不同，那么在乘答案的时候就要多乘一个m.）

• 容斥原理：

即枚举空盒的个数，剩下的随意放置，由于盒子是相同的最后要除以m!
注意到这个式子是一个卷积，所以可以在\(O(nlogn)\)内求出\(S(n,0)\),\(S(n,1)\)......

• 性质
  \(n^{k}=\sum_{i=0}^{k}C(n,i)*S(k,i)*i!\)

左边就是k个球可以任意放置在n个盒子里。
右边就是枚举非空盒子的数量i，那么把k个球放在i个盒子（盒子不同，需要乘上一个i!）里面再乘上选出i个非空盒子的方案数。
(有了这个东西，我们可以很方便的维护一些东西。)

>公式化简：

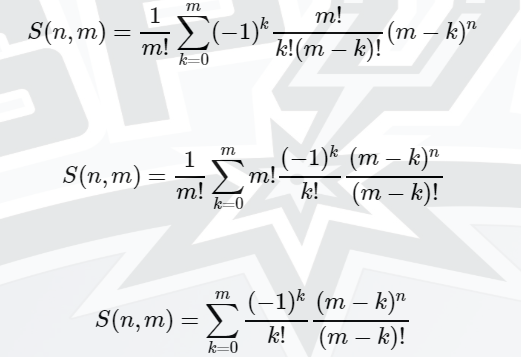
看到这个东西很想卷积，这样我们就能用FFT/NTT求在O(nlogn)的时间内求S2(n,m)的某一行啦。
那么令f(i)=(-1)^i/i! g[i]=i^n/i! 那么S2(n)=f.g 第m项系数就是S2(n,m)
NTT求第二类斯特林数模板：洛谷P5395 第二类斯特林数·行：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#define LL long long
using namespace std;
const int N=1e6+10;
const LL P=167772161,yg=3;
LL n,fac[N],inv[N],f[N],g[N],S2[N];
LL bin[N];

LL power(LL x,LL p) {
    LL ret=1;
    for (;p;p>>=1) {
        if (p&1) ret=(ret*x)%P;
        x=(x*x)%P;
    }
    return ret;
}

void NTT(LL *a,LL n,LL op) {  //NTT:系数a数组，长度为n，op=1求值op=-1插值
    for(LL i=0;i<n;i++) bin[i]=(bin[i>>1]>>1)|((i&1)*(n>>1));
    for(LL i=0;i<n;i++) if(i<bin[i]) swap(a[i],a[bin[i]]);
    for(LL i=1;i<n;i<<=1) {
        LL wn=power(yg,op==1?(P-1)/(2*i):(P-1)-(P-1)/(2*i)),w,t;
        for(LL j=0;j<n;j+=i<<1) {
            w=1;
            for(LL k=0;k<i;k++) {
                t=a[i+j+k]*w%P;w=w*wn%P;
                a[i+j+k]=(a[j+k]-t+P)%P;a[j+k]=(a[j+k]+t)%P;
            }
        }
    }
    if(op==-1) {
        LL Inv=power(n,P-2);
        for(LL i=0;i<n;i++) a[i]=a[i]*Inv%P;
    }
}

int main()
{
    cin>>n;
    fac[0]=inv[0]=1;
    for (int i=1;i<=n;i++) fac[i]=fac[i-1]*i%P,inv[i]=power(fac[i],P-2);
    for (int i=0;i<=n;i++) f[i]=(power(-1,i)+P)%P*inv[i]%P;
    for (int i=0;i<=n;i++) g[i]=power(i,n)*inv[i]%P;

    LL len=1;while(len<(n+1)<<1) len<<=1;

    NTT(f,len,1); NTT(g,len,1);
    for (int i=0;i<len;i++) S2[i]=(f[i]*g[i])%P;  //求f.g的卷积为S2
    NTT(S2,len,-1);

    for (int i=0;i<=n;i++) printf("%lld ",S2[i]);  //求第n行的斯特林数
    return 0;
}

例子
CF932E

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#define ll long long
#define re register
#define il inline
#define db double
#define fp(i,a,b) for(re int i=a;i<=b;i++)
#define fq(i,a,b) for(re int i=a;i>=b;i--)
using namespace std;
const int mod=1e9+7,N=5005;
int n,k,S[5005][5005];
ll ans;
il int gi()
{
  re int x=0,t=1;
  re char ch=getchar();
  while(ch!='-'&&(ch<'0'||ch>'9')) ch=getchar();
  if(ch=='-') t=-1,ch=getchar();
  while(ch>='0'&&ch<='9') x=x*10+ch-48,ch=getchar();
  return x*t;
}
il void Pre()
{
  S[0][0]=1;
  fp(i,1,k)
      fp(j,1,i) S[i][j]=(S[i-1][j-1]+1ll*j*S[i-1][j]%mod)%mod;
}
il ll ksm(re ll S,re ll n)
{
  re ll T=S;S=1;
  while(n)
    {
      if(n&1) S=S*T%mod;
      T=T*T%mod;
      n>>=1;
    }
  return S;
}
il ll jc(re int l,re int r)
{
  re ll res=1;
  fp(i,l,r) (res*=i)%=mod;
  return res;
}
int main()
{
  n=gi();k=gi();
  Pre();
  fp(i,1,min(k,n))
      (ans+=1ll*S[k][i]*jc(n-i+1,n)%mod*ksm(2,n-i)%mod)%=mod;
  printf("%lld\n",ans);
  return 0;
}