Zero-shot Label-Aware Event Trigger and Argument Classification

Motivation

• 事件分类依赖于大量注释，因此zero-shot很重要
• 之前的zero-shot方法很依赖于从已知的事件类型推测新的事件类型，但是一旦新的类型与所有已知类型都不相似，那么这类方法就会失效。
• 本文使用事件参数的定义和上下文语义来表示标签，并且不基于任何训练数据

Task

• 预定义：事件触发词类型集合\(\mathcal{E}\)，参数类型集合\(\mathcal{R}\)，实体类型\(\mathcal{T}\)
• 输入：句子\(S\)，触发词\(v\)，事件参数\(a\)
• 输出：对触发词和事件参数分类为制定类别

Model

模型分为两部分：预处理和预测。

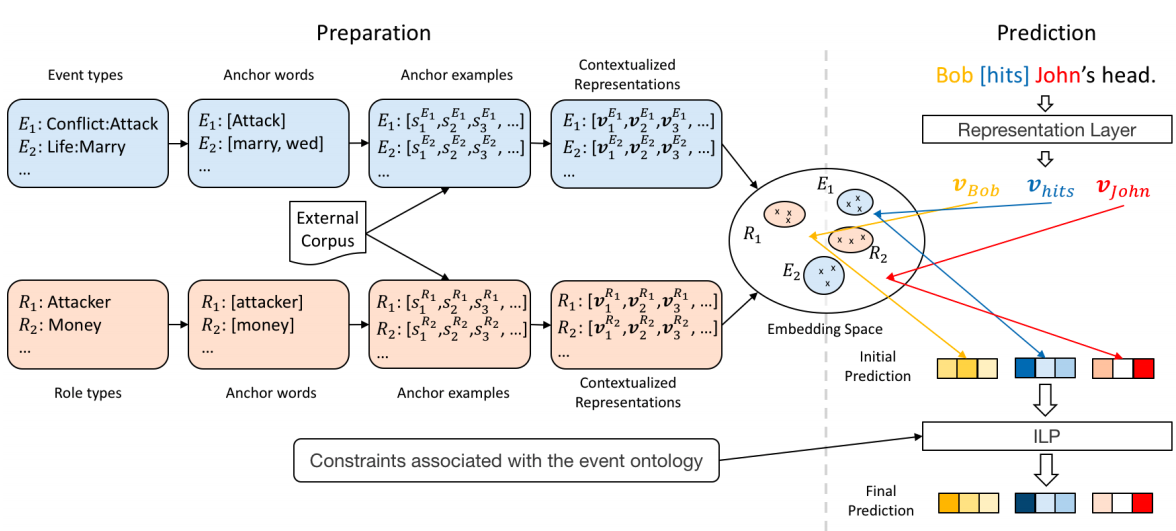
首先对于每一个事件类型，选择trigger word和同义词作为anchor word，从外部资源中抽取包含anchor word的若干句子，用预训练模型编码这些句子，根据编码结果得到标签的聚类中心，每个事实描述中的词通过与聚类中心计算距离得到预测概率，然后使用整数线性规划来约束预测结果。

Contextualized Representation Generation

作者对于trigger word和argument的词有不同的上下文表示策略。

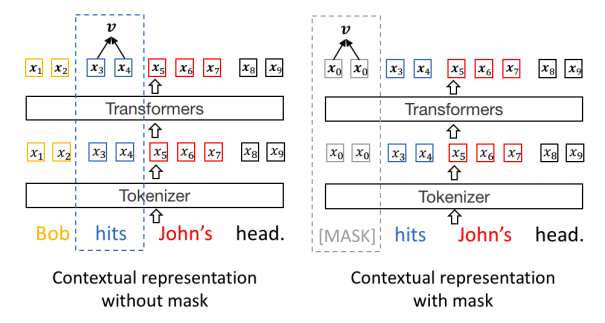
对于trigger word，表示为encoder编码整个句子后trigger word的位置的向量；对于事件参数，模型把参数位置用\(\mathtt{[MASK]}\)来代替。

Prediction

判别trigger word属于哪个事件

\[f(t, E) = \mathrm{Cos\_Dist}(t, \frac{\sum_{v \in \mathcal{V}^E} v }{|\mathcal{V}^E|} ) \]

其中\(\mathcal{V}^E\)事件类型\(E\)的聚类点集合。

同理，判断事件参数：

\[f(a, R) = \mathrm{Cos\_Dist}(a, \frac{\sum_{v \in \mathcal{V}^R} v }{|\mathcal{V}^R|} ) \]

作者提出了一些限制。

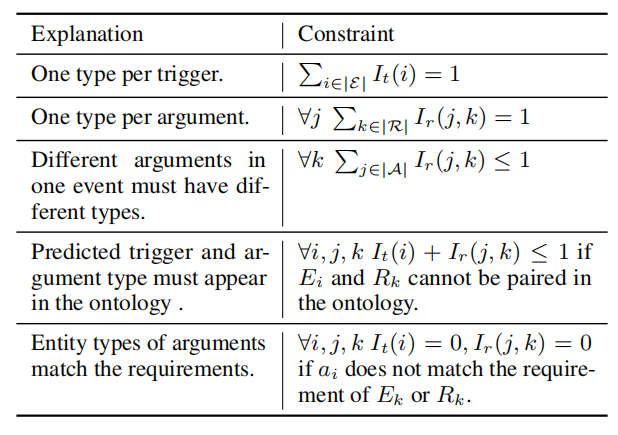
用整数线性规划在满足一些限制条件的情况下最大化下面目标函数

\[\arg\max_{I_t,I_a} \sum_{j \in |\mathcal{A}|} ( \sum_{i \in |\mathcal{E}|} f(t, E_i) \cdot I_t(i) \cdot \lambda + \sum_{k \in |\mathcal{R}|} f(a_j , R_k) \cdot I_a(j, k)) \]

其中\(I_t, I_a\)分别表示预测的事件类型和参数矩阵。
第一部分让相似度大的事件类型预测概率也大，第二部分让相似度大的参数概率也大。

Experiments

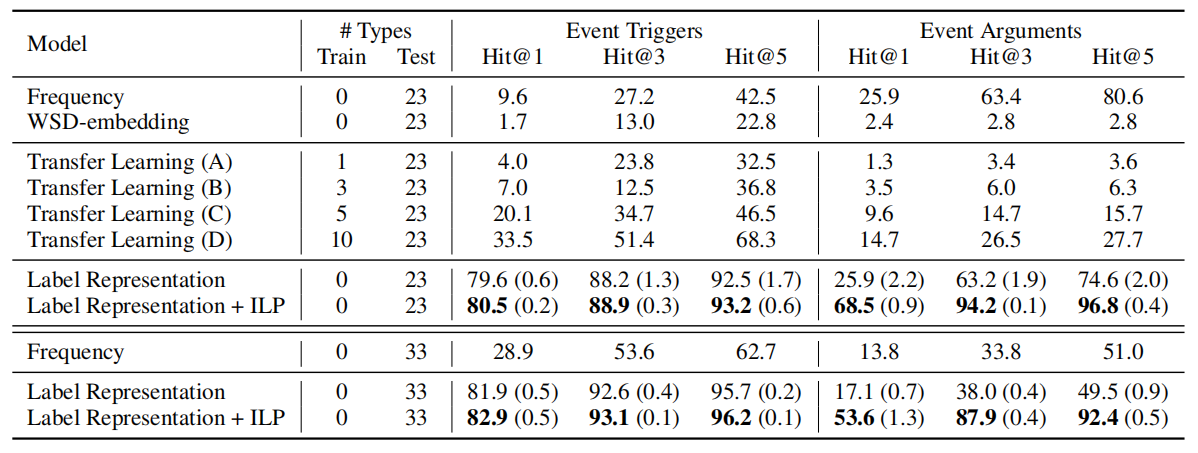
两种setting：拿其中一部分（最少见的22个事件类型）作为测试集和全部都作为测试集。