Learning from the Best: Rationalizing Prediction by Adversarial Information Calibration

最近看了一些关于Rationale的方法，选取其中一篇写个笔记

---

Motivation

• 之前的rationale的方法中，选择器和预测器的结果来自于预测对真实答案的比较，这样的探索空间非常大。
• 通常用于实现rationale流畅性的正则化器以相同的方式对待所有相邻的token pairs。这通常会导致选择不必要的token，因为它们与rationale token相邻。

针对上面两个问题，作者提出了 InfoCal：

• 使用两个模型：selector-predictor model 和 guider，让他们得到的表征相互接近
• 引入“信息瓶颈”模块，鼓励模型学习least-but-enough的特征
• 另外使用自然语言模型来计算相邻token之间的相关性，并修改正则化系数

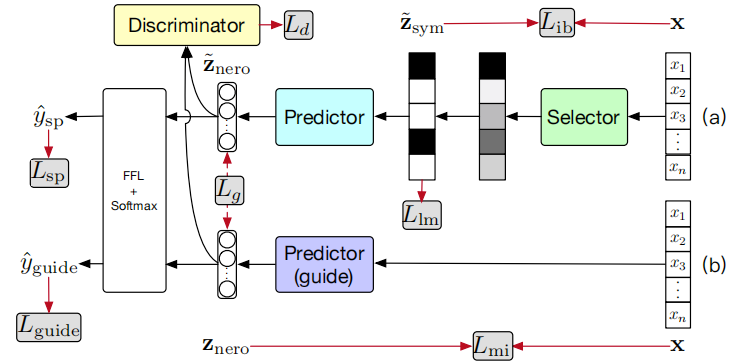
InfoCal: Selector-Predictor-Guider with Information Bottleneck

Selector

输入\(x=(x_1,x_2,\dots,x_n),y\)，selector学习\(p(\tilde{z}_{sym}|x)\)并输出\(p_i\)表示第\(i\)个词属于rationale的概率，基于概率可以使用gumbel softmax采样得到rationale mask矩阵：

\[u_i \sim U(0,1), g_i = -\log (-\log (u_i))\\ m_i = \frac{\exp((\log p_i + g_i) / \tau)}{\sum_j \exp((\log p_j + g_j) / \tau)} \]

然后获取rationale筛选过的表征\(\tilde{z}_{sym} = (m_1x_1,m_2x_2,\dots, m_nx_n)\)

Predictor

\[\tilde{z}_{nero} = \mathbf{Pred}(\tilde{z}_{sym})\\ p(\hat{y}|\tilde{z}_{sym}) = \mathbf{Softmax}(W_p \tilde{z}_{nero} + b_p) \]

\(\hat y\)就是预测的目标，由于中间有采样步骤，因此交叉熵损失通过琴声不等式可以计算出一个上界：

\[L_{sp} = − \frac{1}{K} \sum_k \log p(y^{(k)}_{sp} | x^{(k)})\\ = − \frac{1}{K} \sum_k \log \mathbb{E}_{\mathbf{Sel}(\tilde{z}^{(k)}_{sym} |x^{(k)})} p(y^{(k)}_{sp} |\tilde{z}^{(k)}_{sym})\\ \le −\frac{1}{K} \sum_k \mathbb{E}_{\mathbf{Sel}(\tilde{z}^{(k)}_{sym} |x^{(k)})} \log p(y^{(k)}_{sp} |\tilde{z}^{(k)}_{sym}), \]

Guider

Guider模型学习一个\(\mathbf{Pred}_{G}\)，然后根据预测采样得到一个稠密向量\(z_{nero}\)。

\[h = \mathbf{Pred}_G(x),\mu = W_m h + b_m,\sigma = W_s h + b_s\\ u \sim \mathcal{N}(0, 1), z_{nero} \sim u \sigma + \mu\\ p(\hat y_{guide} | z_{nero}) = \mathbf{Softmax}(W_p \tilde{z}_{nero} + b_p) \]

其中最后一步的预测层和Predictor共享参数。

\[L_{guide} \le −\frac{1}{K} \sum_k \mathbb{E}_{p(z^{(k)}_{nero} |x^{(k)})} \log p(y^{(k)}_{guide} |z^{(k)}_{nero}) \]

Information Bottleneck

这个模块目标是学习least-but-enough的特征。
形式化为最小化\(I(x,\tilde{z}_{sym}) - I(\tilde{z}_{sym}, y))^2\)，第一项是为了让模型学习尽可能少的特征，第二项是让模型学习尽可能有用的特征，其中第二部分在\(L_{sp}\)中实现，所以只需要考虑第一项。

\[I(x, \tilde{z}_{sym}) = \mathbb{E}_{x,\tilde z_{sym}} \left [ \log \frac{p(\tilde z_{sym}|x)}{p(\tilde z_{sym})} \right] \]

由于\(p(\tilde z_{sym})\)难以计算，所以用变分分布\(r_{\phi}\)代替：

\[I(x, \tilde{z}_{sym}) \le \mathbb{E}_{x,\tilde z_{sym}} \left [ \log \frac{p(\tilde z_{sym}|x)}{r_{\phi}(z)} \right]\\ L_{ib} = \sum_i \sum_{\tilde z_i} p(\tilde z_i | x)\log \frac{p(\tilde z_i | x)}{r_{\phi}(z_i)} \]

同理，对guide模型的约束：

\[L_{mi} = I(x, z_{nero}) \le \mathbb{E}_{z_{nero}} \left [ \log \frac{p(z_{nero}|x)}{p(z_{nero})} \right ] = = 0.5(\mu^2 + \sigma^2 − 1 − 2 \log \sigma) \]

Calibrating Key Features via Adversarial Training

我们希望告诉选择器仍然缺少什么类型的信息或错误地选择了什么。由于我们已经使用信息瓶颈原则来鼓励\(z_{nero}\)编码来自“最少但足够”特征的信息，如果我们还要求\(\tilde z_{nero}\)和\(z_{nero}\)编码相同的信息，那么我们将鼓励选择器选择“最少但足够”的离散特征。为了达到这个目的，我们使用了一种基于对抗的训练方法。因此,我们采用一个额外的鉴别器神经模块，称为\(D\)，它将\(\tilde z_{nero}\)或\(z_{nero}\)作为输入，并分别输出0或1。鉴别器可以是任何可微神经网络。我们模型中的生成器是由输出\(\tilde z_{nero}\)的选择器-预测器组成的。与发生器和鉴别器相关的损失为:

\[\begin{align} L_d &= − \log D(z_{nero}) + \log D(\tilde z_{nero})\\ L_g &= − \log D(\tilde z_{nero}) \end{align} \]

Regularizing Rationales with Language Models

用自然语言模型来建模两个相邻token之间应该连续的概率，而不是视为完全一样的权重

\[L_{lm} = −\sum_i m_{i−1} \log p_{lm}(m_ix_i| x_{< i}) \]

Experiments

BeerAdvocate

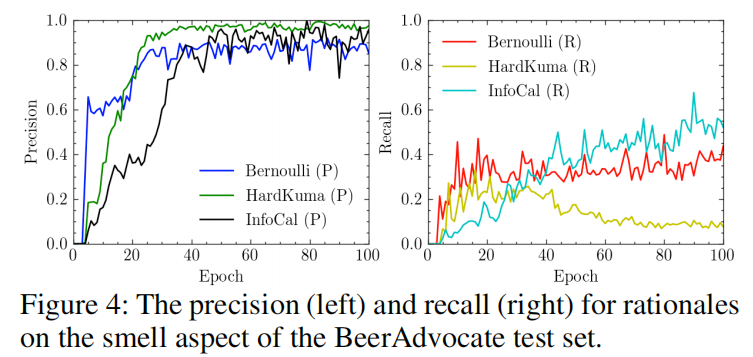
• rationale 选择评估

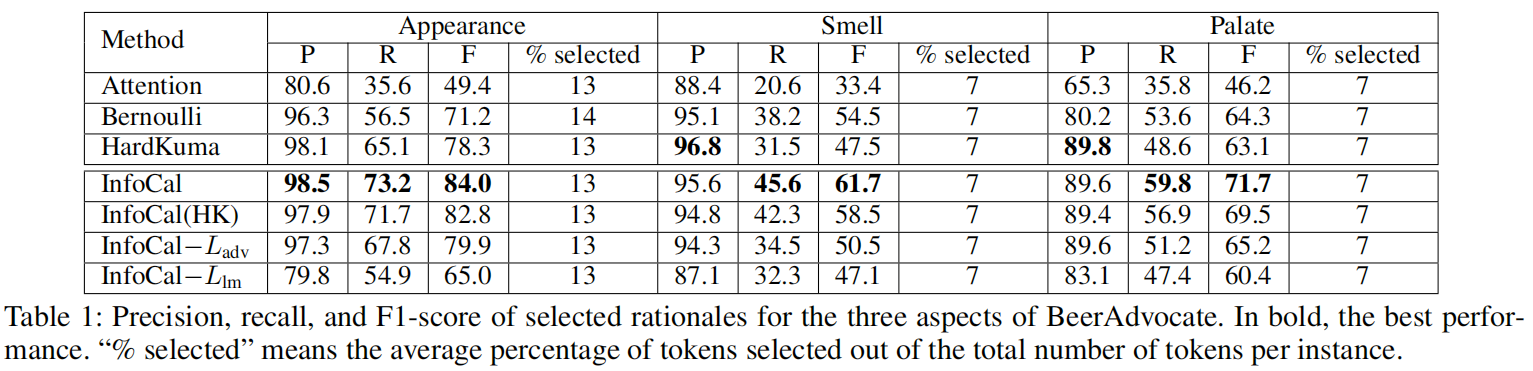
• 模型表现

Legal Judgement Prediction

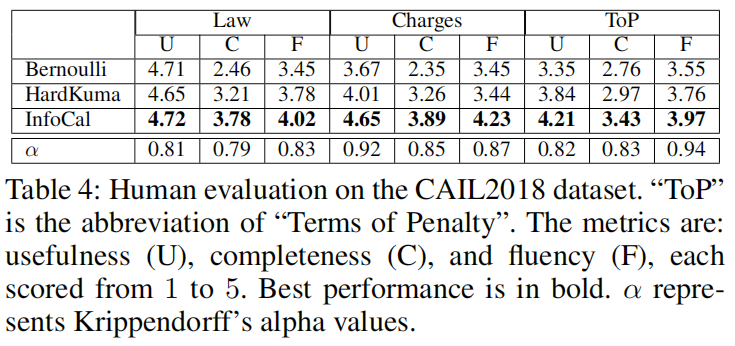
• 三个子任务表现
  

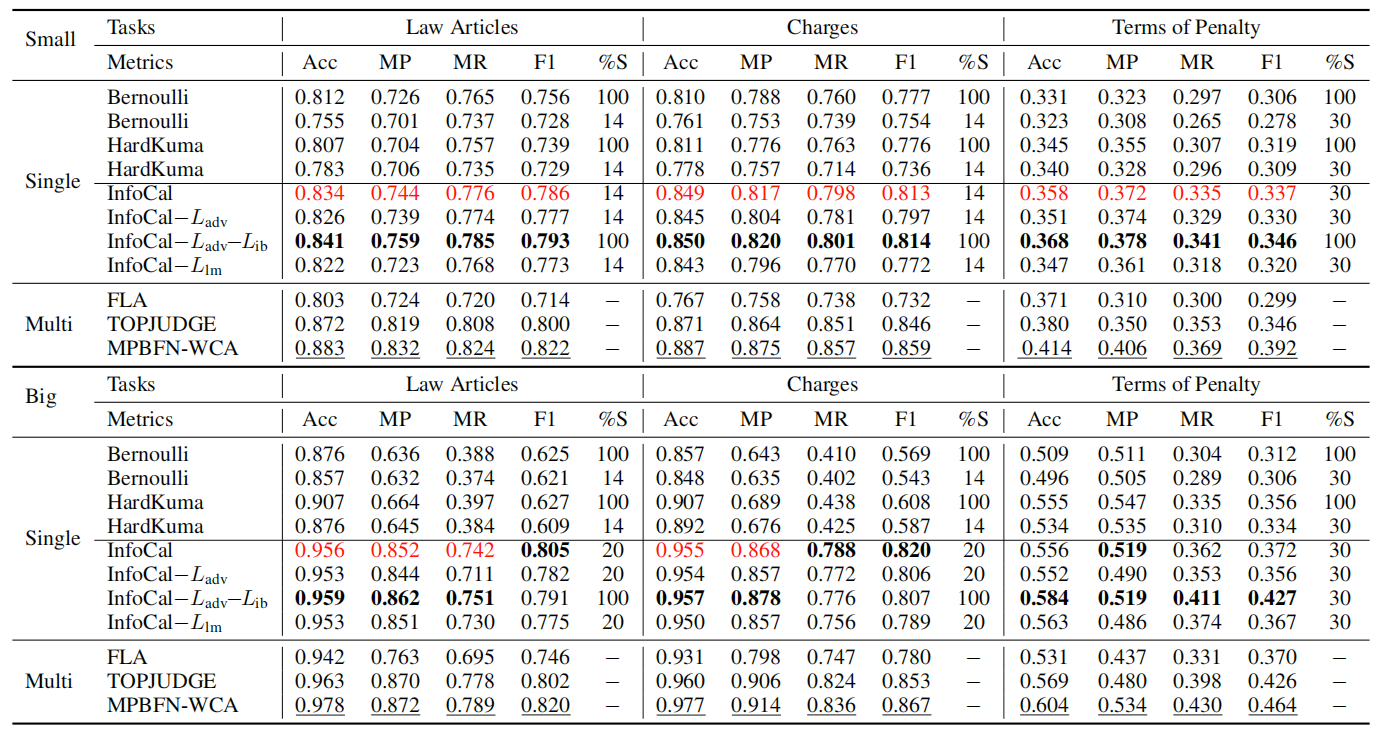
• rationale选择