From What to Why: Improving Relation Extraction with Rationale Graph

Motivation

• 之前的研究很少关注“为什么模型会预测某一个输出”，基于 rationale graph 可以提供更好的可解释性
• 实体类型和触发词是预测实体关系的两个重要信息

如：

Augustus	is	the	youngest	of	five	children	of	Hawkins
PERSON						Trigger		PERSON

从人的角度考虑，当我们注意到主语和宾语实体都是PERSON，以及上下文中出现的触发词children时，我们的第一反应是它们可能具有亲子关系。
因为我们知道，亲子关系只有可能在“人-人”之间存在，而这种先验知识可以作为二部图增强关系抽取模型。

Rationale Graph（RAG）

现在基于假设：数据中标注了，如图所示

• 实体
• 实体关系
• 触发词 trigger

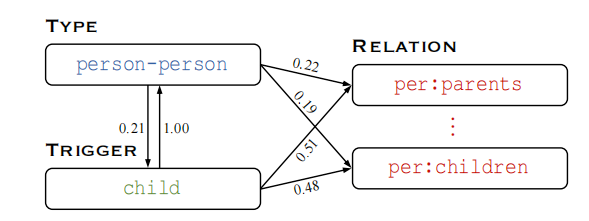
首先，构建每个instance的二部图，然后放入全局二部图中。
从总数据中统计出\(type \rightarrow relation\)、\(trigger \rightarrow relation\)、\(trigger \leftrightarrow type\)的数量，然后对RAG上所有的边进行normalization，保证每个点的出边概率之和为1：

\[\overline{w}_{ij} = p(r_j|t_i) = w_{ij} / \sum_{j'} w_{ij'} \]

图上四种边\(\varepsilon \leftarrow \{ \mathcal{M}_{tp2re}, \mathcal{M}_{tg2re},\mathcal{M}_{tp2tg},\mathcal{M}_{tg2rp}\}\)

Relation Extraction with RAG

• 预测实体对儿类别（如PERSON-PERSON）
• 预测trigger
• 联合trigger和实体对的预测结果计算实体关系，更新实体对儿和trigger表示（这一部分基于motivation中的推理依据）

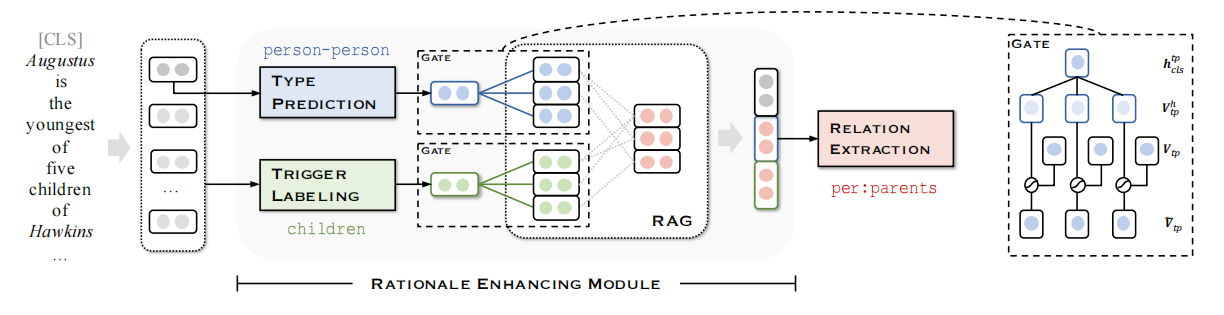
Encoding Module

用BERT作为特征编码器，输出\(H \in \mathbb{R}^{n \times d}\)，其中包含一个\(h_{cls} \in \mathbb{R}^d\)

Rationale Enhancing Module

这一部分是本文主要的模型创新。
原理增强模块由两个增强分支和一个原理集成单元组成。在每个分支中，首先预测输入实例的模式(类型或触发器)，然后计算实例属于RAG中的每个模式的模式概率。集成单元的目标是根据图的模式概率和图中的理论基础，收集理论基础增强特征，最终进行关系提取。

Type Enhancing Branch

预测实体对儿类型：

\[h_{cls}^{tp} = \tanh (\mathbf{MLP} (h_{cls}))\\ p_{tp} = \mathbf{Softmax} (\mathbf{MLP} (h_{cls}^{tp})) \]

\(n_{tp}\)表示已知的所有实体对儿类型。

Trigger Enhancing Branch

在预测句子的trigger时，作者使用两个序列标注模型，分别标注开始节点和结束节点。
首先将原来的bert输出序列和CLS标记的表示拼接：\(\overline{H} = [H; h_{cls}]\)。然后开始节点和结束节点的边界被设定为两边的CLS。
计算每个点作为开始和结束的概率：

\[p_{sta} = \mathbf{Softmax}(\mathbf{MLP}(\overline{H}))\\ p_{end} = \mathbf{Softmax}(\mathbf{MLP}(\overline{H})) \]

每个span综合起来的表示，\(h_{pre}^{tg} \in \mathbb{R}^{d}\)：

\[h_{pre}^{tg} = \frac{1}{2} (p_{sta} + p_{end}) \overline{H}\\ \]

计算与每个已知的trigger的相似度

\[p_{tg} = \mathbf{Softmax}(\mathbf{sim}(h_{pre}^{tg}, V_{tg})) \]

\(p_{tg} \in \mathbb{R}^{n_{tg}}\) is the probability of the given instance corresponding to each known trigger

当遇到某个没见过的trigger，这种方法也可以将它与之前见过的trigger联系在一起，考虑他们之间的相关性。

Rationale Intergration

以type为例，预测type与某个预定的type（假设叫\(t\)）越相似，那么对\(t\)的更新就越多。

用概率加成的文本侧（原文叫text-side）的类型表示

\[V_{tp}^h = p_{tp}^{\mathsf{T}} h_{cls}^{tp} \]

计算相似度

\[\delta_{tp} = \mathbf{Sigmoid}(\mathbf{MLP}([V_{tp};V_{tp}^h])) \]

门控更新

\[\tilde{V}_{tp} = (1 - \delta_{tp}) \circ V_{tp} + \delta_{tp} \circ V_{tp}^h \]

同理，对应的trigger部分，计算得到\(\tilde{V}_{tg}\)(怀疑作者这里是写错了，原文写的是\(\overline{V}_{tg}\))
用R-GCN更新节点表示

\[V_{tp}, \overline{V}_{tg}, \overline{V}_{re} = \mathbf{R-GCN}(\tilde{V}_{tp}, \tilde{V}_{tg}, V_{re}) \]

然后加权每一个关系的embedding表示，权重系数一部分来自于文本侧得到的属于某一type/trigger的概率，另一部分来自于rationale图上的边的权重。

\[h_{tp} = p_{tp}M_{tp2re}\overline{V}_{re}\\ h_{tg} = p_{tg}M_{tg2re}\overline{V}_{re} \]

文章中并没有用到\(M_{ty2tg}\)和\(M_{tg2tp}\)？

Classification Head

\[h_{re} = [h_{cls}; h_{tp}; h_{tg}]\\ p_{re} = \mathbf{SoftMax}(\mathbf{MLP}(h_{re})) \]

Training Objectives

由于明确知道文本中的trigger，因此可以施加对比学习，使得目标trigger的表示与\(h_{pre}^{tg}\)更近，引入一个margin \(M\)。

\[d = ||h^{tg}_{pre} − v_{tg}^{mat}||_2\\ \mathcal{L}_{mat} = (1 − \mathbb{I}_{mat})(\max\{0, m − d\})^2 + (\mathbb{I}_{mat})(d)^2 \]