Semi-supervised New Event Type Induction and Event Detection

Motivation

• 手动构造事件类型和标注数据成本非常高
• 手动标注的时间覆盖率比较低

Method

本文提出了一个基于VQ-VAE的半监督事件检测方法。

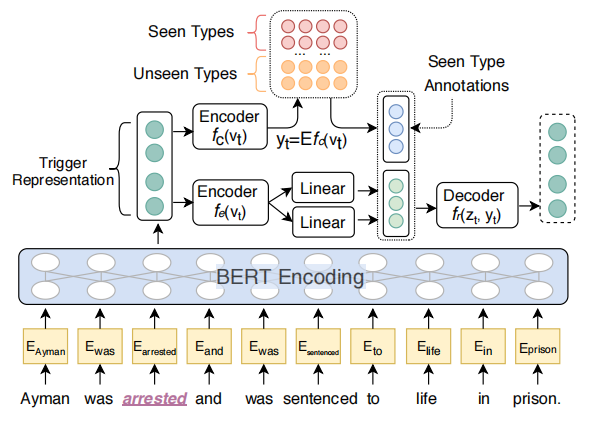
Trigger Representation Learning

句子表示为\(s = [w_1, \dots, w_n]\)，用所有subtoken的表示的平均值作为trigger word \(w_i\)的表示。

Event Type Prediction with Vector Quantization

每个事件类型的隐藏空间表示向量\(E \in \mathbb{R}^{k \times d}\)，\(e_i\)为第\(i\)个事件的表示向量，\(k\)为事件类型数量。

假设有\(m\)个已知的事件（seen type，因为本文的设定包含挖掘未看到的事件类型，因此涉及到seen type和unseen type，分别表示在训练集中标注了的事件类型和没标注的类型）。

已知候选触发词\(t\)和上下文表示\(v_t\)，用一个编码器\(f_c(v_t) \in \mathbb{R}^{d}\)计算对应的事件类型表示，然后通过离散的潜在事件表示计算事件类型分布

\[y_t = \text{Softmax}(E^{[1:k]} \cdot f_c(v_t)) \]

训练损失表示为

\[\mathcal{L}_c = \sum_{(t,\tilde{y}_t) \in D_s} - \tilde{y}_t \log (y_t) + \sum_{t \in D_u} \max (y_t^{[1:m]}) - \max ( y_t^{[m:k]}) \]

上式第一部分为seen type的交叉熵损失，第二项为让unseen type中距离t最近的那个事件比seen type中最近的事件距离t的表示更近。

另外一部分损失，更新code block和防止预测的隐藏向量在离散事件类型表示中来回跳跃

\[\mathcal{L}_{vq} = ||\text{sg}(f_c(v_t)) - e_i||^2 + ||f_c(v_t) - \text{sg}(e_i)||^2 \]

Variational Autoencoder as Regularizer

为了让事件类型预测不过拟合于seen type，使用VQ-VAE，其直觉是，每个事件提及都可以在潜在的变分嵌入\(z\)及其对应的类型分布\(y\)的条件下生成

SS-VQ-VAE的推理包含两个阶段，\(q(z|t)\)（由事件提及预测隐层向量）和\(p(t|y,z)\)（由事件类型分布和隐藏表示生成事件提及）。

对于seen type

\[\log p(t, y) \ge \log p(t|y, z) − \text{KL}(q(z|t)||p(z)) = −\mathcal{L}(t, y) \]

对于unseen type

\[\log p(t) \ge \sum_y q(y|t)(−\mathcal{L}(t, y)) − q(y|t) \log q(y|t) = −\mathcal{L}(t) \]