A Causal Lens for Controllable Text Generation

Motivation

本文的工作涉及到两个任务：属性条件生成、文本风格迁移。

之前的大量工作在很大程度上分别研究了这两个问题开发了不同的条件模型，但容易产生有偏见的文本.

本文从因果的角度将两个任务统一起来，分别视为在因果图上的“干预”和“反事实”两部分，然后再将框架应用于一个比较具有挑战性的场景中：部分混淆因子可见。

Introduction

本文研究的可控文本生成任务包括：

1. attribute-conditional generation。生成的文本需要包含一个指定属性。
2. text attribute transfer。在尽量保留原始文本语义的情况下，重新生成句子，要求包含某个属性。
   这两个任务最终都是要生成\((attribute, text)\)对儿。

用\(x\)表示生成的句子，\(a\)表示属性，之前的工作大多学习的是\(p(x|a)\)，这种形式很容易学习到虚假关联，如在传记文本中，男女性别差异可能造成职业差异，最终导致模型泛化性能下降，或对下游任务造成社会偏见。

之前也有工作去研究过这个问题，但是他们大多都适用于特定的混淆因子，比如性别；或者依赖于额外的信号，如完全可观测的混淆因子。

本文在不同的因果层级实现这两个任务：

1. attribute-conditional generation，用干预表示，\(p(x|do(a))\)
2. text attribute transfer，用反事实表示，\(p(x'|x, a(x), a')\)

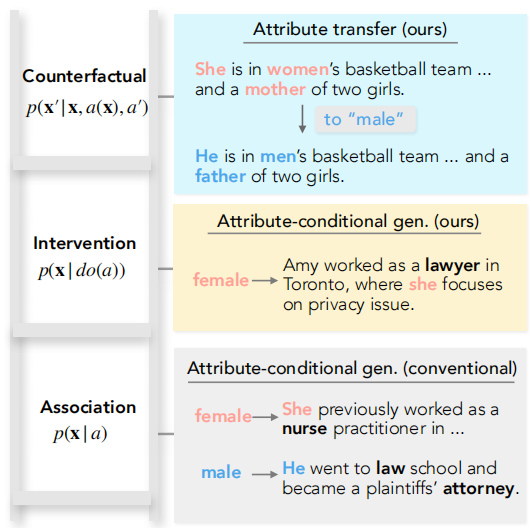
在实际应用中，我们不可能完全观测到所有的confounders，所以这里引入一个更加现实的setting：我们只能在1%到5%的samples中观测到混淆。

Causal Framework for Controllable Text Generation

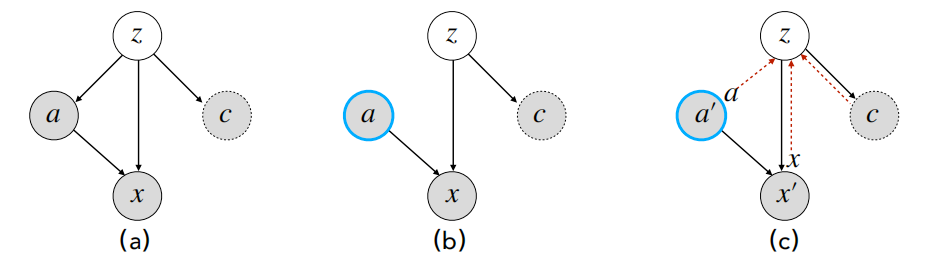
Structual Causal Model

• 这里假设treatment \(a\)是一个二元变量，可以是\(a \in \{ 0, 1\}\)，也可以是一个prompt。
• 由于在现实中高纬混淆变量\(z\)可能难于估计，所以我们引入一个代理变量\(c\)来间接估计\(z\)。

SCM定义了一个联合分布：

\[p_{\theta}(x,a,z,c) = p_{\theta}(x|a, z) p_{\theta}(a|z) p_{\theta}(c|z) p_{0}(z) \]

式中

• \(p_{\theta}(c|z)\)只有在sample的\(c\)可以被观测到时才有
• \(p_0(z)\)表示混淆变量遵循常理，服从一个先验的标准高斯分布。
• 用VAE推断潜在变量\(z\)
  • 存在一个变分分布\(q_{\phi}(z|x,z,c)\)
  • 在\(c\)可观测的samples上训练一个预测器，用来预测不可观测的sample中的\(c | (x, a)\)，但在本文中，我们将\(c\)设置为一个虚值

Inference (I): Intervention for Attribute-Conditional Generation

这一部分讨论属性条件生成在因果图上是如何作用的。

使用后门调整进行干预：

\[p_{\theta}(x|do(a)) = \sum_z p_{\theta}(x|a, z) p(z) \]

• 首先，采样\(z \sim p(z)\)
  • 通过一个GAN网络\(p_{\mathrm{GAN}}(z)\)采样，\(z \sim q_{\phi}\)
• 然后，解码\(x \sim p_{\theta}(x|a, z)\)

Inference (II): Counterfactual for Text Attribute Transfer

这个任务可以被形式化为反事实预测。

• 首先，推断上下文context，在这里，context可以被理解为\(z\)，也就是计算\(q_{\phi}(z|x, a, c)\)
• action，将\(a\)设置为\(a'\)，
• 最后，预测\(x' \sim p_{\theta}(x'|a',z)\)，将\(z\)设置为分布的平均值。

Learning

Variational auto-encoding objective

\[\mathcal{L}_{vae}(\theta, \phi) = \mathbb{E}_{z \sim q_{\phi}}[\log p_{\theta}(x|a, z) + \lambda_a \log p_{\theta} (a|z) + \lambda_c \log p_{\theta} (c|z)] - \lambda_{kl} \mathrm{KL}(q_{\phi}||p_{0}) \]

当\(c\)不可观测时，\(\lambda_c = 0\)。

Counterfactual objectives

上面的建模收到两个方面的影响：

• \(p_{\theta}(x|a,z)\)可能对\(a\)不是很敏感，因为训练数据的文本中已经存在属性相关信息了。
• 需要将不同attribute时的\(z\)联系在一起

从上面的角度考虑，作者继续提出了以下学习目标：

• 训练一个属性分类器\(f(x,a)\)，判断句子\(x\)是否包含属性\(a\)
  \[ \mathcal{L}_{cf-a}(\theta, \phi) = \mathbb{E}_{z \sim q_{\phi}, x' \sim p_{\theta}(x' | z, a')} [f(x', a')] \]
  由于句子离散，没有梯度，因此引入，Gumbel-softmax approximation
• 不同属性的句子对应的潜在变量应该不变，最小化两个潜在变量分布的距离：
  \[ \mathcal{L}_{cf-z}(\theta, \phi) = -\mathbb{E}_{z, z'}[d(z, z')] \]
  \(d\)函数用于评估两个分布的距离。
• 希望通过\(z'\)能够重建变量\(c\)
  \[ \mathcal{L}_{cf-c}(\theta, \phi) = \mathbb{E}_{z'} [\log p_{\theta} (c|z')] \]

最终学习目标：

\[\mathcal{L}(\theta, \phi) = \mathcal{L}_{vae} + \gamma_a \mathcal{L}_{cf-a} + \gamma_z \mathcal{L}_{cf-z} + \gamma_c \mathcal{L}_{cf-c} \]