【题目背景】:中秋节了,CCC老师决定去送礼。
【问题描述】:一个被分为 n*m 个格子的月饼盒,第 i 行第 j 列位置的格子里面有 a [ i , j ]个月饼。本来CCC老师打算送这盒月饼给某人的,但是就在要送出月饼盒的前一天晚上,一只极其可恶的老鼠夜袭月饼盒,有部分格子被洗劫并且穿了洞。CCC老师必须尽快从这个月饼盒里面切割出一个矩形月饼盒,新的月饼盒不能有洞,并且CCC老师希望保留在新月饼盒内的月饼的总数尽量多。
【题目任务】:请帮CCC老师设计一个程序 计算一下新月饼盒最多能够保留多少月饼。
【文件输入】:第一行有两个整数 n、m。第 i + 1 行的第 j 个数表示 a [ i , j ],如果这个数为 0 ,则表示这个位置的格子被洗劫过。其中: 0 ≤ a [ i , j ]≤ 1000
【文件输出】:输出最大月饼数
【样例输入】
3 4
1 2 3 4
5 0 6 3
10 3 4 0
【样例输出】
17
PS:对于40%的数据,N ,M≤80
对于60%的数据,N ,M≤400
对于100%的数据,N,M≤1000
题解:
对于(i,j)这个格子,我们如果将以它为某矩形底边的一个格子,它向上可以达到高为h[i][j],我们把这个看成一条高为h[i][j]的一条线段,让这条线段向左右尽可能长地摆动,假设他能够摆动的长度分别为L[i][j]和R[i][j],这样能够得到一个以(i,j)为底边一点的最大矩阵(即可以确定矩形的左上脚坐标和右下脚坐标),这样我们用递推就可以一次性算出这个矩阵的权值。如下图。
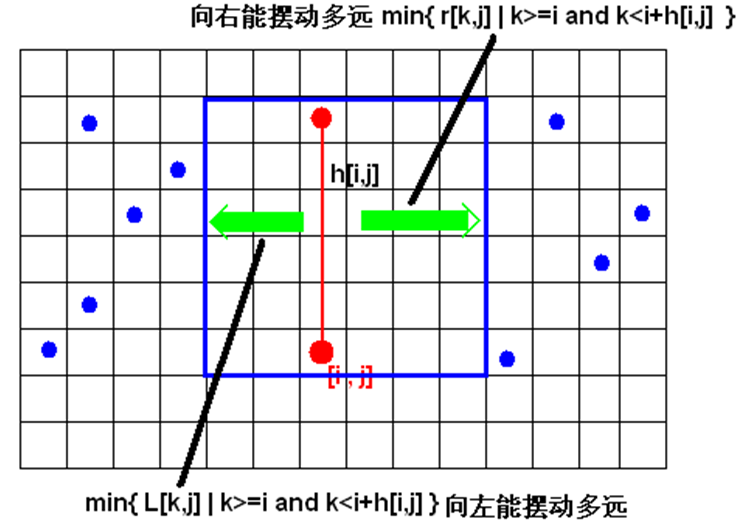
h[i,j]、L[i,j]、R[i,j]都可以递推得到:
当格子中的数为0的时候h[i][j]=0,否则h[i][j]=h[i-1][j]+1;
当格子中的数为0的时候L[i][j]=0,否则L[i][j]=L[i][j-1]+1;
当格子中的数为0的时候R[i][j]=0,否则R[i][j]=R[i][j+1]+1;
代码贴上:
#include<cstdio>
#include<iostream>
using namespace std;
int x2,x1,y1,y2,c,n,m,a[1005][1005],h[1005][1005],r[1005][1005],l[1005][1005],ans,maxx;
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%d",&c);
a[i][j]=c+a[i-1][j]+a[i][j-1]-a[i-1][j-1];
if(c==0) h[i][j]=0;
else h[i][j]=h[i-1][j]+1;
}
for(int j=1;j<=m;j++)
if(h[i][j]==0) l[i][j]=0;
else l[i][j]=l[i][j-1]+1;
for(int j=m;j>=1;j--)
if(h[i][j]==0) r[i][j]=0;
else r[i][j]=r[i][j+1]+1;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(h[i][j]>0)
{
if(h[i][j]>1)
{
l[i][j]=min(l[i][j],l[i-1][j]);
r[i][j]=min(r[i][j],r[i-1][j]);
}
x2=i;y2=j+r[i][j]-1;
x1=i-h[i][j]+1;y1=j-l[i][j]+1;
maxx=a[x2][y2]-a[x2][y1-1]-a[x1-1][y2]+a[x1-1][y1-1];
ans=max(ans,maxx);
}
printf("%d",ans);
return 0;
}
仅为个人见解,若有不好之处,欢迎反映交流!




