Pratt Parser解释器_TDOP_自上而下的运算符优先解析

Partt Parser又称普拉特语法分析器。

指 沃尔-普拉特所编写的论文《Top Down Operator Precedence》中的基于定义优先级运算符的方式解析为AST树的一种语法分析技术。 

 

在执行语法分析器的时候，我们的已经的到了经过词法分析器的结果。

也就是

1+2+3

Token	Type
1	NUM
+	ADD
2	NUM
+	ADD
3	NUM

1-5*3+5

Token	Type
1	NUM
-	MIN
5	NUM
*	MUL
3	NUM
+	ADD
5	NUM

当我们得到单元集合之后，就是需要语法分析器去处理这个单元之间的关系。

Partt解析器则是通过单元优先级规则的一种解析器。

简单的说就是根据每个单元的类型划分为前序和中序，并按照[前序-中序]的规则不断从单元集合的第一位推进到最后一位.

 

 

这个所谓的前序和中序是符号可以出现的位置。

例如

1就是前序

+就是中序

-则是前序，因为减号可以当作负数或者减法符号，所以减法同时是中序。

例子

1+2+3

这个四则表达式中存在了数字和加法两种符号。

我们简单的分析一下前序和中序，以及解释器能够推进的方法。

序列	类型	优先级
前序	1	0
中序	+	1
前序	2	0
中序	+	1
前序	3	0

这个表格中，多出了一个优先级，这个解释器能够推进的根本。除去前序，中序的固定搭配之外，能够推进的秘密就是优先级的高低。

这个优先级是按照，基本的数学规定。

也就是 先算乘除  后算加减

因为 数字也是计算单元的一部分，只不过没有被数学规定计算的优先级，所以默认为最低的。

也就是下表

符号	优先级
NUM	0
+	1
-	1
*	2
/	2

最终合成下表

顺序	符号	优先级
前序	NUM	0
中序	+	1
前序	-[负号]	1
中序	-[减法]	1
中序	*	2
中序	/	2

解释器根据符号的优先级和符号结合性形成了AST

例一

1+2+3

AST就是

 

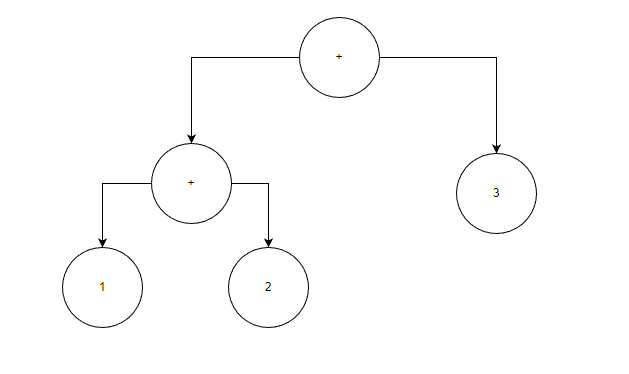
例二

1+2*3-4

AST

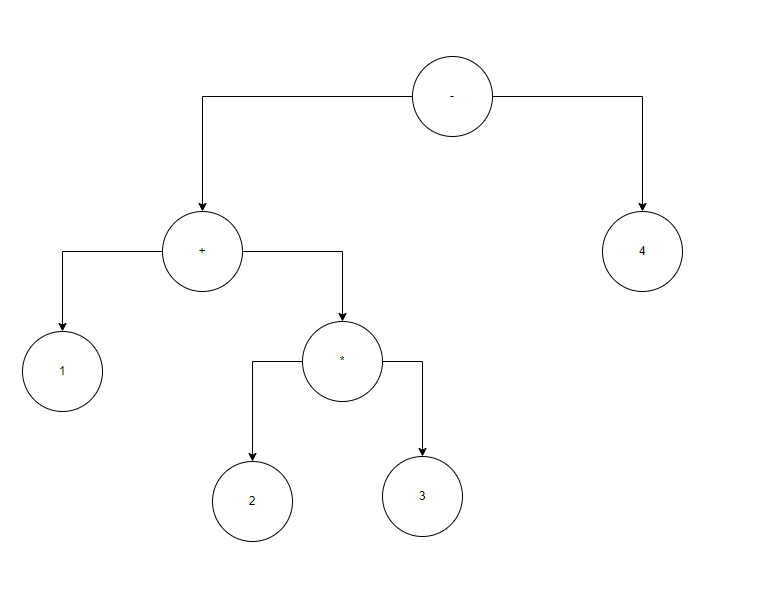
优先级的作用AST树中是分配【当前表达式】是否继续按照【前序-中序】的顺序匹配下一个表达式。

【前序-中序】可以理解为

【前序】生成最顶层叶子节点的左侧表达式

【中序】将【前序】表达式作为最终或者当前表达式的左侧节点，右侧节点并且依旧按照【前序-中序】的顺序匹配。

 这个解释器的结构总是【前序-中序】，一个表达式的开始肯定是一个【前序】处理之后在处理【前序】直到结束或者下一个token优先级大于当前可以执行【中序】。

【中序】则是将【前序】的表达式作为当前结果的左侧表达式，右侧表达式又是从【一个表达式的开始】也就是【前序】开始处理下一个token，换句话说又开始执行【前序-中序】这个结构。

 简单总结下

1.入口【前序-中序】

2.【前序】

3.下一个优先级大于当前【判断是否进入中序】或者token集合不结束.

4.【中序】

5.将【前序】作为左侧表达式

6.执行1，并将结果作为右表达式

7.依次返回

8.出口【前序-中序】

 

优先级为什么要当前的Token级别大于下一个Token级别才可以执行中序。

举例

 

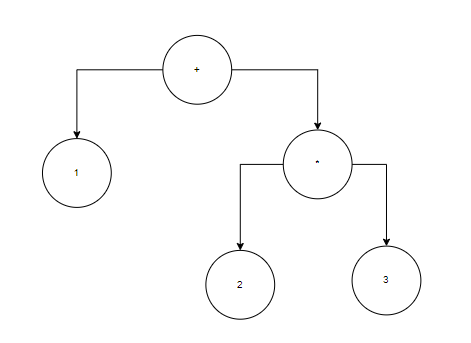
这是一个树状图。

我们可以得到（中序遍历）

1+2*3

 在这个程度上加一呢？

 

 

 

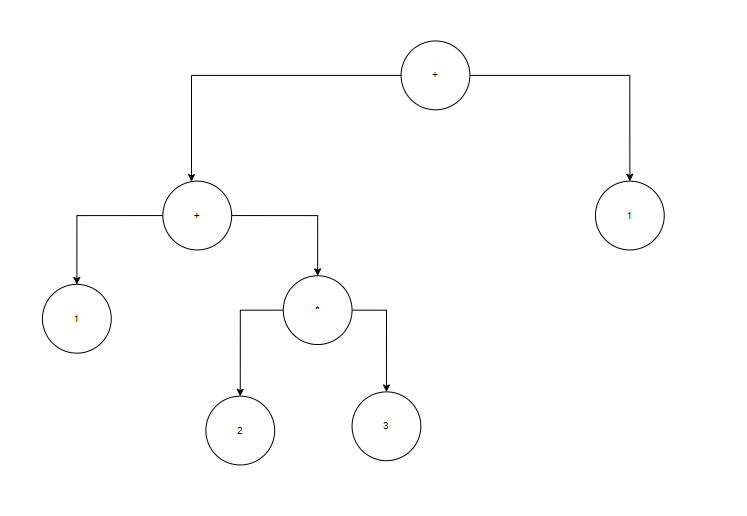
如果是1+2*3*4*5（在表达式1+2*3的基础上添加*4*5）呢

 

 

 

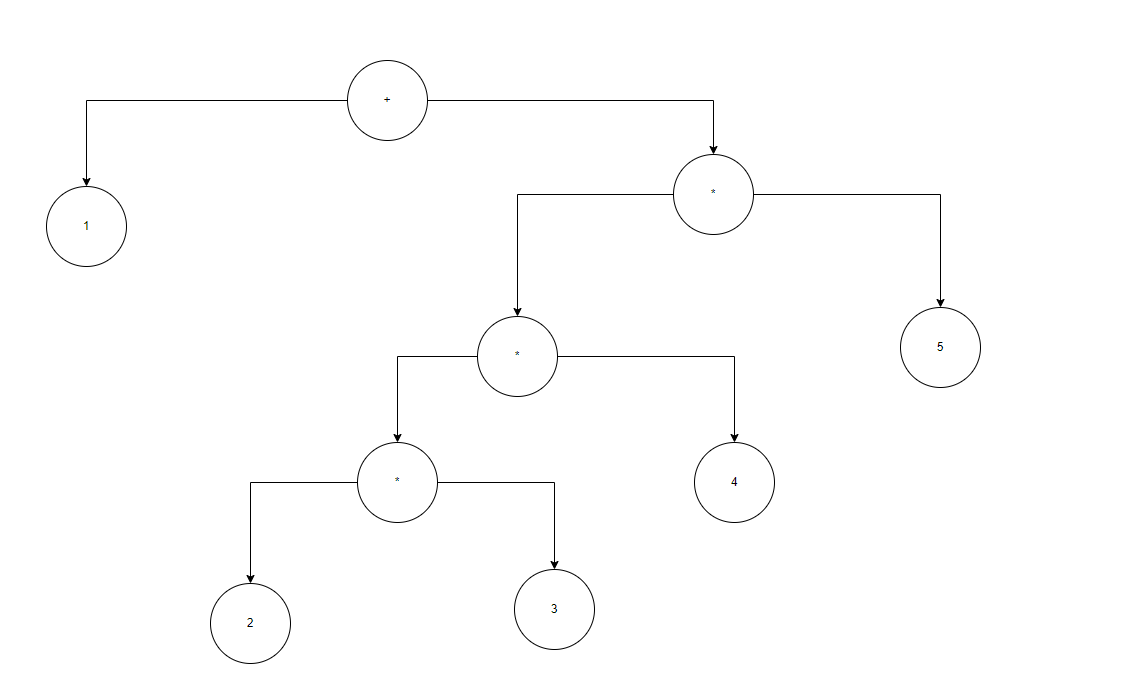
在添加一个表达式时，AST会

1.如果这个表达式是和顶点不同级优先级则会增加叶子层数，改变右侧叶子顶点为最新表达式token，并将原先叶子归为左叶子节点，新加表达式为右侧叶子节点

 

 

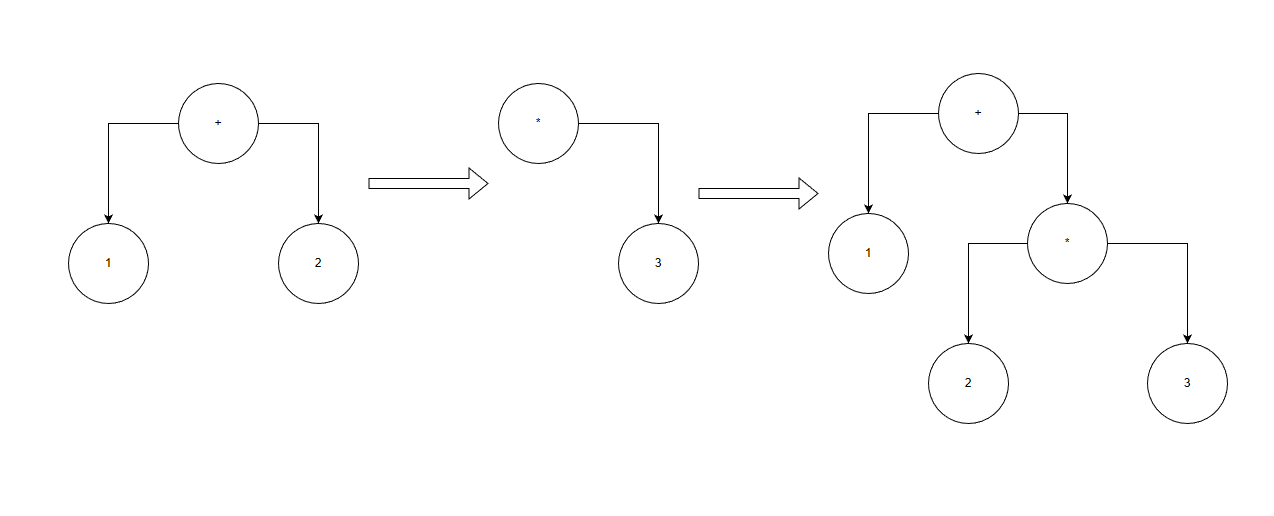
2.如果这个表达式是和顶点同级优先级则是增加叶子层数，改变顶点为最新表达式token和同时原先将左右叶子归为左侧叶子，右侧叶子节点放置新加表达式

 

 

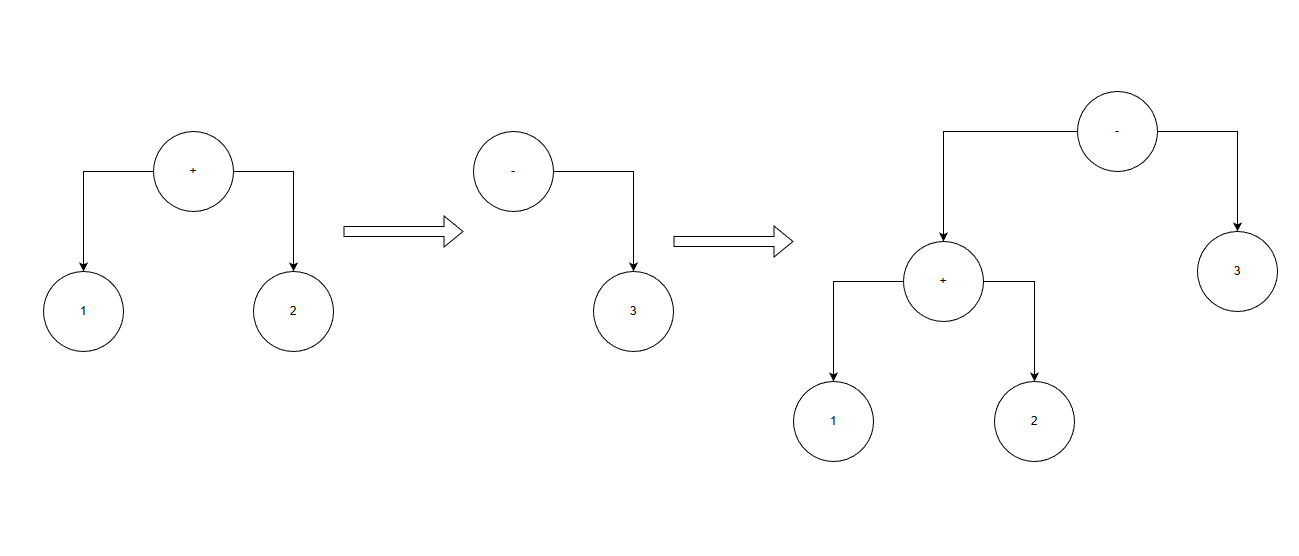
优先级主要是决断二叉树是否更换顶点，打断原有的结构顺序。

括号的作用也就可以在这里直接说明，因为括号也是打断原有括号，括号是前序运算符，所以只需要打断括号后第一个符号的等级，使得可以接纳所有符号直到括号结束。也就是说只需要像默认开始一样函数就OK了。

 

代码层面需要明确知道两个东西，当前符号和下一个符号，以及划分前序，中序，优先级等级 以及对应函数的方法。

代码虽然不多，也是小500了  我直接放代码地址吧

自上而下的运算符优先级分析: 自上而下的运算符优先级分析（也称普拉特解析法 (gitee.com)