添加简单的光
上一节中绘制出来的简直惨不忍睹啊。
但是这一节中,我们就可以实现这样的,看起来更真实了,因为我们添加了光
漫反射

镜面反射

光的类型
点光
可以理解为灯泡,有着固定的位置,发出来的光线到每个点都是不一样的。
L=Q-P
方向光
可以理解为太阳,在大尺度下看,太阳的光到地球和点光没有什么不同。但是我们身处于地面 看太阳,方向可都是一致的...
所以方向光对于每个点是一致的。
L=Q
环境光
因为是计算机中的世界,我们单纯计算两个光是没有办法点亮整个世界的。
按照书中说,最好的例子就是低头看看桌子底下,依旧是可以看到的东西.
所以我们要定义物体每个可以自发光....
那么我们的环境中是怎么计算光的?
是计算每一个点的环境光+点光+方向光。
但是呢,由于光会有损耗,有些光会被吸收。这个是需要介绍物体反射光的类型了
物体反射
物体的反射可以大概分成给哑光,闪亮两者。
木头啊,桌子啊。墙面都是哑光的。
玻璃,车漆,基本都是闪亮的。
这本书中说,一个环境内光的总量是1,环境光是每个物体都有的,点光和方向光均分剩下的。
另外呢,就是光的类型,一个是漫反射,一个是镜面反射,对应哑光和闪亮两种类型。
光的反射的能量或者说反射光的数量,取决于入射角度与物体表面的角度,我们用法线来表示这个面的方向,因为法线总是垂直于面。
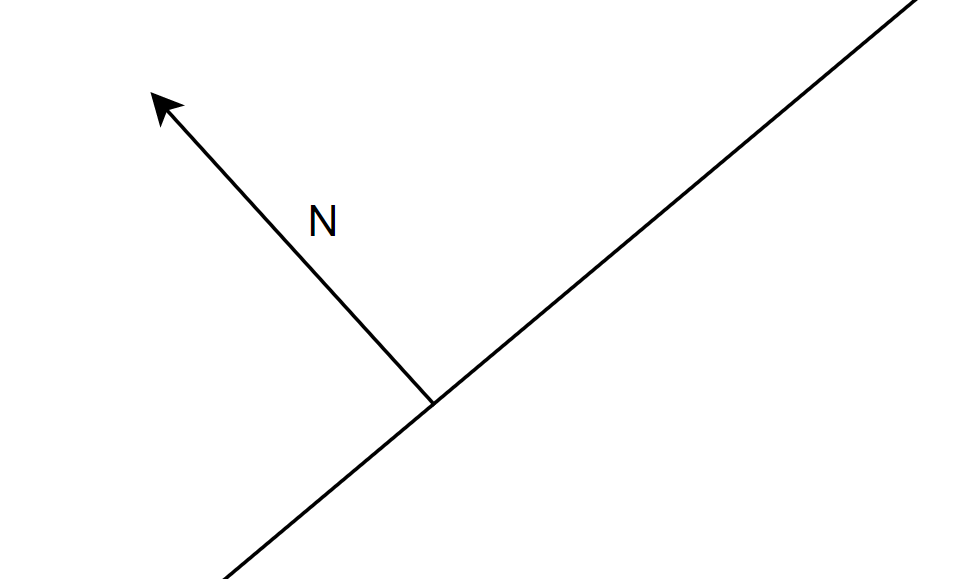
光入射时根据角度将能量,均匀的分布在物体表面。所以当面积越大反射越小,面积越小反射越大。所以我们看到的光实际上是计算光的能量与面积的比
漫反射
当光照射到哑光的物体时,光会沿着每个方向散射回到场景中,所以你从每个角度看哑光物体都是差不多的。
另外光的反射的多少是看角度的。
漫反射分析或者建模就是对反射的计算。由于我们的光线是从画布看到点的过程。
这个反射上实际计算是当画布的某个XY点与圆上一点相交时,光线在点的作用程度是多少。就是我们看到的XY坐标显示的颜色是什么。
简单分析
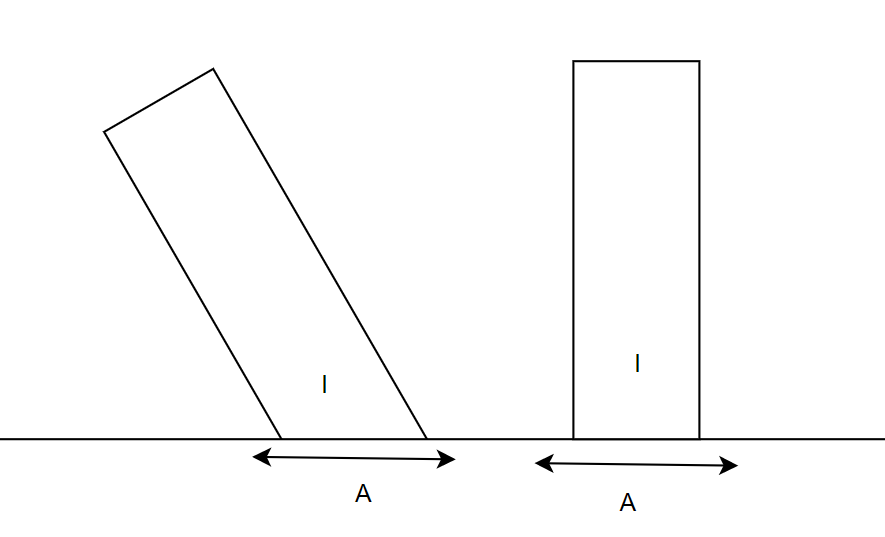
光是能量,我们这个简单绘制中使用I来表示光的强度(能量)。光照射在物体表面的面积用A代替。
由于光不存在宽度,但是存在强度,我们使用一个矩形的宽度代表强度,单位强度的光照射在单位面积的时候的强度与面积是I/A=1,所谓的单位就是1 例如单位元就是半径为1,单位强度就是矩形宽为1,单位面积是面积为1.
当光入射的时光线L与法线N逐渐垂直时(平行),lim I/A =∞(无限) 因此比值为0
我们看下图
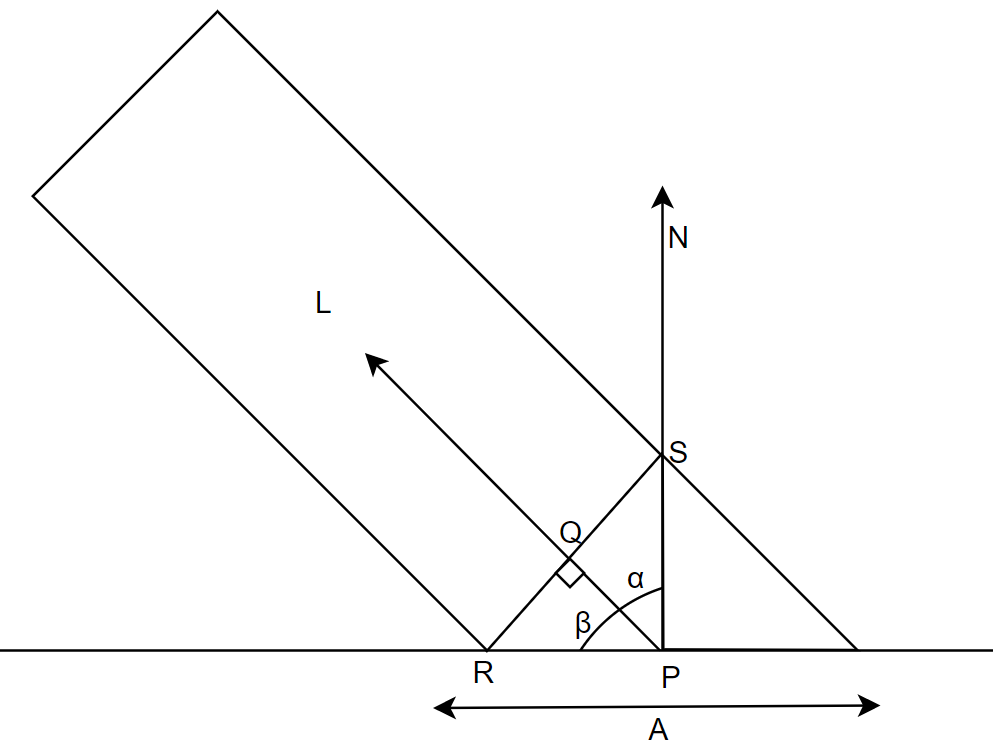
我们将光定义为漫反射,光会沿着入射角度反射,当光线L以β角度照射点P,光将能量均匀的分布在A面积上。
虽然说求这个点P的漫反射实际上就是计算I/A的值。那么I/A实际上是什么呢?我总不能直接I/A吧,A是面积,但是我们求点P,所以也可以计算I/P的面积,但是点P多大?这怎么算。所以这个路子也不对。
从图上看β角度入射,漫反射会以α角度反射。我们来看:
这些都是单位向量,我们假设点P处于中间位置,所以 线段RS是光线L的宽度是I(i),RP的宽度是A/2。RQ的长度I(i)/2。
因为∠RQP是90度,∠RPN也是90度,∠β+∠α等于90度,所以∠PRQ等于∠α。
我们现在能够和I/A扯上关系的RQ/RP(存在I,A),这也是∠PRQ的cos值,也就是cos(a)的值,任意角的三角函数请放置在单位元中
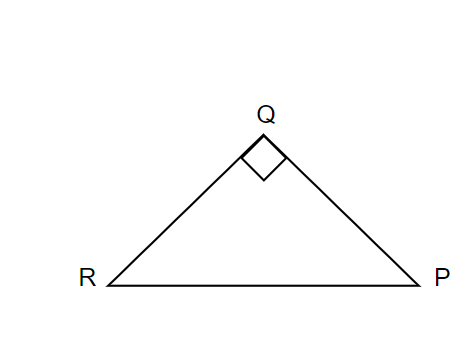
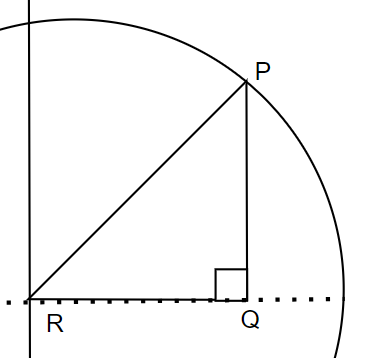
cos(a)=RQ/RP=I/2/A/2,分子分母上下乘以一个数值不变,所以上下同时乘以2等于cos(a)=I/A.
I/A=cos(a),这个比值得到了一个函数。
光是没有宽度的,实际上只是一个值而已。光线传播过程是一个向量准确一点就是图中的L,也就是向量L,所以COS(a)等于向量L和法线N的点乘除向量L乘向量N。
L dot N等于|L| |N|*COS(a)
即cos(a)=L dot N/ |L| *|N|=I/A
只需要用光的强度乘上cos(a)就可以得到这个光的漫反射。
我们解决了漫反射的计算方法,下一步就计算这个点接受的或者呈现出所有光的方法。
之前说 光的总量是不变,一个点的光是环境光+N点光+N方向光,其中方向光是对每个点都是相同所以,也是已知,但是需要计算漫反射。点光也是需要计算,因为知道了点乘所以需要求出光向量即可。
因为环境光是物体自带的,就不参与漫反射的计算过程。
最终
环境光+Σ (其他光的强度(N*L/ |L| *|N|))
其中: 其他光包括方向光,点光。
法向量
因为我们用的是球,球的表面的法向量非常简单就是表面点到球心。
即 P-C
代码
所以 我们来构建代码吧,因为说光的总量是1,且只能存在一个环境光,所以我们就定义
class Light { public Vector3D Direction { get; set; } public Vector3D Position { get; set; } public LightEnum LightType { get; set; } public double Intenesity { get; set; } }
光的类型
enum LightEnum { Ambient, Point, Directional }
定义三个光,强度总量为1
List<Light> lightlist = new List<Light> { new Light(){ LightType= LightEnum.Ambient,Intenesity=0.2 }, new Light(){ LightType= LightEnum.Point,Intenesity=0.6,Position=new Vector3D(2,1,0) }, new Light(){ LightType= LightEnum.Directional,Intenesity=0.2,Direction=new Vector3D(1,4,4) } };
我们需要添加一个算计光强的函数
/// <summary> /// 计算光 /// </summary> /// <param name="p">表面点P</param> /// <param name="n">法向量</param> /// <returns>强度</returns> double ComputeLighting(Vector3D p, Vector3D n) { double i = 0; Vector3D l = new Vector3D(); //遍历所有的光 foreach (var light in lightlist) { //不同的写法 if (light.LightType == LightEnum.Ambient) { i += light.Intenesity; } else { if (light.LightType == LightEnum.Point) { l = light.Position - p; } else { l = light.Direction; } var dot = Vector3D.DotProduct(n, l); if (dot > 0) { i += light.Intenesity * dot / (n.Length * l.Length); } } } return i; }
首先对于每个点遍历所有光,因为环境光是不需要计算漫反射所以排除,直接加到光量总和。
因为点光对每个点都是不同的,所以需要单独计算光向量。
方向光也说过对于每个点都是一样的,所以直接使用方向光的照射角度。
然我们在光线追踪函数下使用
Color tracrray(Vector3D origin, Vector3D dline, double min, double max) { double closet = double.PositiveInfinity; sharp claset_sharp = null; foreach (var item in sharplist) { var gp = IntersectRayShere(origin, dline, item); if (gp.X >= min && gp.X <= max && gp.X < closet) { closet = gp.X; claset_sharp = item; } if (gp.Y >= min && gp.Y <= max && gp.Y < closet) { closet = gp.Y; claset_sharp = item; } } if (claset_sharp == null) { return Colors.White; } var p = origin + (closet * dline); var n = p - claset_sharp.center; n = n / n.Length; var cl = ComputeLighting(p, n); return Color.FromRgb((byte)(cl * claset_sharp.color.R), (byte)(cl * claset_sharp.color.G), (byte)(cl * claset_sharp.color.B)); }
光直接作用在点上,所以直接影响到每个通道的值。
最后我们就得到了头图的效果,看起来还不错。至少能看出来是一个球了。
镜面反射
镜面反射对应的闪亮的效果。
镜面反射分析
镜面反射的过程就是入射角度根据法线做的镜像。

那怎么计算镜面反射呢? 我们又能看到多少呢?
镜面反射不同于漫反射在任何角度上看到的是一样的,所以不考虑角度的,镜面反射则是需要的。
因为视线看点P是存在角度,有可能这个角度和反射R不重合。
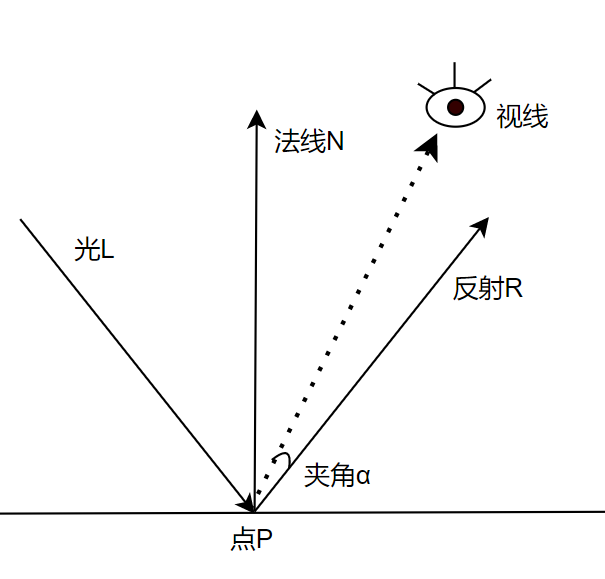
在看到闪亮的东西时,只有越贴合光线的反射角度看到越亮,远离反射角度或者说夹角α越大看起来无光泽,夹角α越小光泽越大。
这个夹角α可以根据视线向量和反射R的点乘来确定。
但是反射R的向量是怎么确定呢?
为了方便计算向量之间的夹角,我们把入射光的向量反过来。并将光L分解为向量Ln+向量Lp。
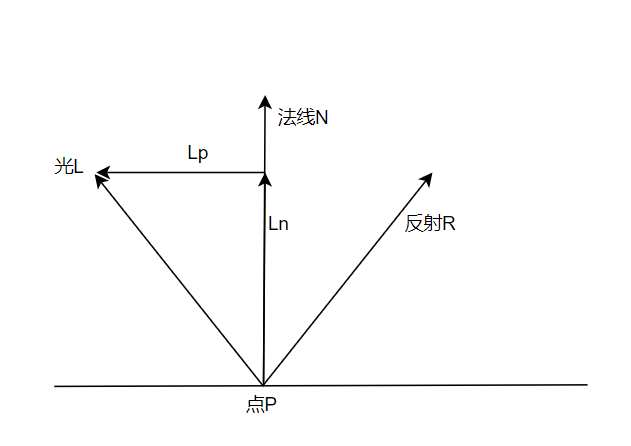
我们知道反射R是L的镜像,既然lp+ln=l,那么肯定-lp+ln=反射R
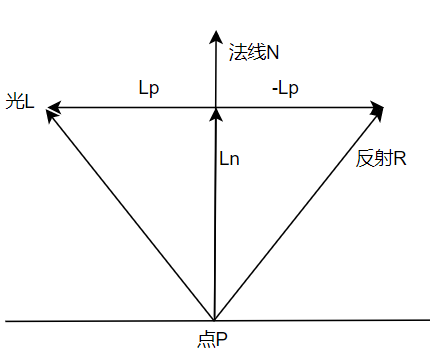
求lp必须要求LN,才可以因为ln=l-ln,
所以ln的长度计算公式如如下
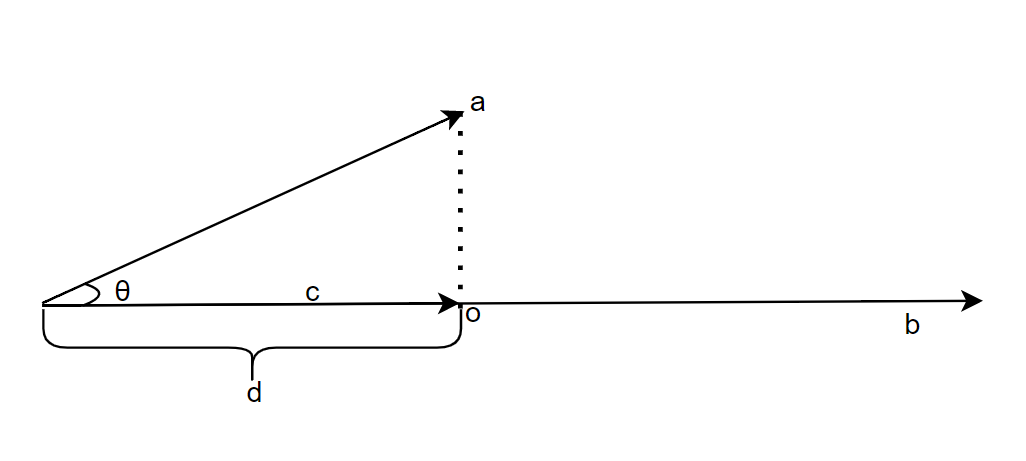
\[\overrightarrow{c}=d\dfrac{\overrightarrow{b}}{\left| b\right| }\]
\[ d=\left| a\right| \cos \left( \theta \right)\]
\[\cos \left( \theta \right) =\dfrac{\overrightarrow{a}\cdot \overrightarrow{b}}{\left| a\right| \left| b\right| }\]
建立联立方程
\[ \overrightarrow{c}=\left| a\right| \dfrac{\overrightarrow{a}\cdot \overrightarrow{b}}{\left| a\right| \left| b\right| }\dfrac{\overrightarrow{b}}{\left| b\right| }\]
即
\[\overrightarrow{c}=\left| a\right| \dfrac{\overrightarrow{a}\cdot \overrightarrow{b}}{\left| a\right| \left| b\right| }\overrightarrow{b}\dfrac{1}{\left| b\right| }\]
最终得
\[\overrightarrow{c}=\dfrac{\overrightarrow{a}\cdot \overrightarrow{b}}{\left| b\right| ^{2}}\overrightarrow{b}\]
带入我们实际的镜面反射模型后,|N|2等于1所以直接等于\[N(N \cdot L)\]
求得Ln就可以求出Lp,等于L-Ln=Lp
这样也就求出反射R=-Lp+Ln或者Ln-Lp
\[R=N(N\cdot L)-(L-N(N \cdot L))\]
\[R=2N(N \cdot L)-L\]
夹角
我们知道反射R,剩下就是视线的问题,视线就是我们发射的向量p。
这个非常好办。
求这个夹角α还是点积公式。
即\[\cos \left( a\right) =\dfrac{\overrightarrow{p}\cdot \overrightarrow{R}}{\left| p\right| \left| R\right| }\]
光泽
我们看一个闪亮的物体时,在不同角度下有不同亮度。
在漫反射中不存在光泽,只是对光的反射而已。镜面反射则是需要一个光泽来体现夹角α的大小。
我们使用的是cos函数,因为cos(0°) = 1和cos( ±90°) = 0,如果我们再加上一些小小的改变比如给cos函数加一个幂
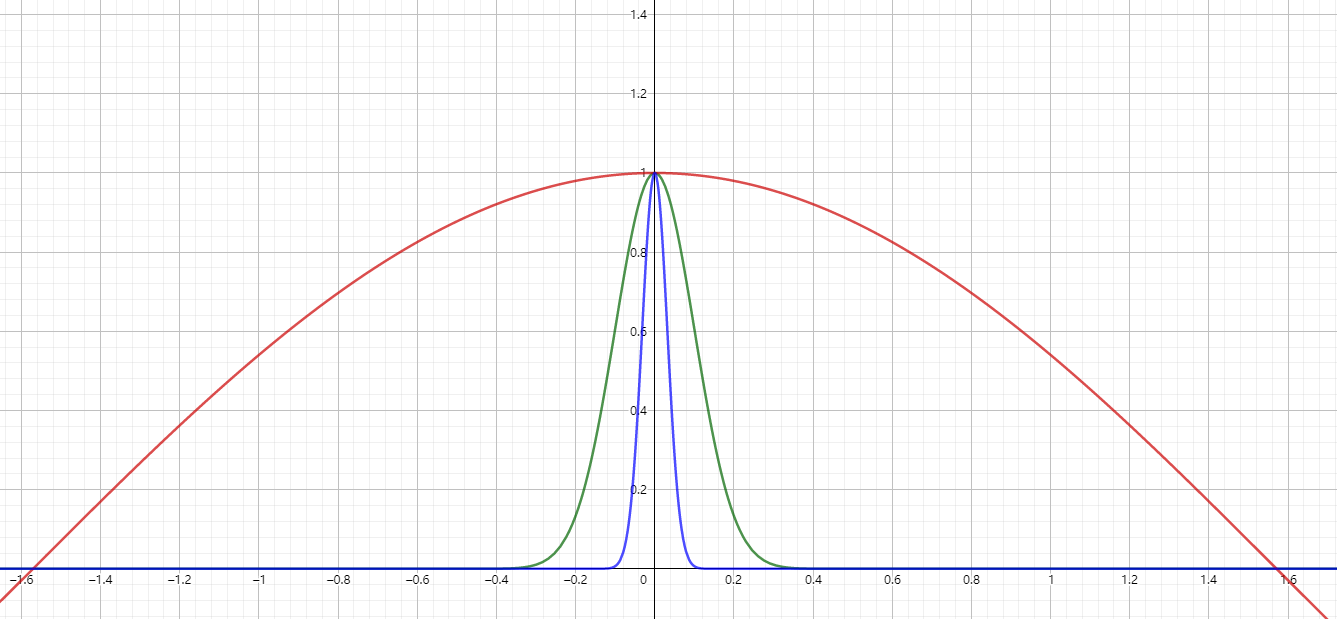
cosx的X值越大,突起越明显就以为特闪亮。
比如说红色是默认为1
绿色就是100
蓝色则是1000了
所以构建物体还是需要定义一个反射x。
而且在运算时小于0就不要添加了。光也没有负强度数..
\[\left( \dfrac{\overrightarrow{p}\cdot \overrightarrow{R}}{\left| p\right| \left| R\right| }\right) ^{s}\]
代码
class sharp { public Vector3D center { get; set; } public double radius { get; set; } = 1; public Color color { get; set; } public double specular { get; set; } }
修改物体反射程度
List<sharp> sharplist = new List<sharp> { new sharp() { center = new Vector3D(0, -1, 3), color = Colors.Red,specular=500 }, new sharp() { center = new Vector3D(2, 0, 4), color = Colors.Blue,specular=500 }, new sharp() { center = new Vector3D(-2, 0, 4), color = Colors.Green ,specular=10}, new sharp(){center=new Vector3D(0,-5001,0), radius=5000,color=Color.FromRgb(255,255,0) ,specular=1000}, };
添加镜面反射
double ComputeLighting(Vector3D p, Vector3D n, Vector3D v, double s) { double i = 0; Vector3D l = new Vector3D(); foreach (var light in lightlist) { if (light.LightType == LightEnum.Ambient) { i += light.Intenesity; } else { if (light.LightType == LightEnum.Point) { l = light.Position - p; } else { l = light.Direction; } var dot = Vector3D.DotProduct(n, l); if (dot > 0) { i += light.Intenesity * dot / (n.Length * l.Length); } if (s != -1) { var r = 2 * Vector3D.DotProduct(n, l) * n - l; var dotv = Vector3D.DotProduct(r, v); if (dotv > 0) { i += light.Intenesity * Math.Pow(dotv / (r.Length * v.Length), s); } } } } //可以设置大1为1 //i>1?1:i return i; }
对颜色每个通道应用光强度
Color tracrray(Vector3D origin, Vector3D dline, double min, double max) { double closet = double.PositiveInfinity; sharp claset_sharp = null; foreach (var item in sharplist) { var gp = IntersectRayShere(origin, dline, item); if (gp.X >= min && gp.X <= max && gp.X < closet) { closet = gp.X; claset_sharp = item; } if (gp.Y >= min && gp.Y <= max && gp.Y < closet) { closet = gp.Y; claset_sharp = item; } } if (claset_sharp == null) { return Colors.Transparent; } var p = origin + (closet * dline); var n = p - claset_sharp.center; n = n / n.Length; var cl = ComputeLighting(p, n, -dline, claset_sharp.specular); //保证颜色上下限正确 var M = Color.FromRgb((byte)(Math.Min(255, Math.Max(0, cl * claset_sharp.color.R))), (byte)(Math.Min(255, Math.Max(0, (cl * claset_sharp.color.G)))), (byte)(Math.Min(255, Math.Max(0, (cl * claset_sharp.color.B))))); return M; }
然后得到了一个头图的镜面反射效果
漫反射计算机图形学入门_3D渲染指南: 由C#作为编程语言,WPF作为输出。 计算机图形学入门3D渲染指南 - Gitee.com
镜面反射计算机图形学入门_3D渲染指南: 由C#作为编程语言,WPF作为输出。 计算机图形学入门3D渲染指南 - Gitee.com

