渲染球体

综述

这一章节，东西不少，画出圆（实际上是球），又没用圆的方程

主要是体现在视口的定义上。说的较为简单。至少我是可以看明白🤣。

另外就是视口到画布，计算过程简单，容易理解。

剩下就是向量与圆相交的部分。

视口

文中有个例子就是眼看风景，你觉非常好看。想要画下，但由于你没有这技能。

于是采用固定木框作为固定视角，木框内覆盖渔网格，画布上也覆盖同样的渔网格保证同样位置大小。

再通过固定视角观察木框的每一个网格的（混合？平均？）颜色在绘制到画布上。

>>>>>>>>>

这个例子作者就是表达出，视口到画布的过程。

你的眼睛是存在于3D空间的原点（x:0,y:0,z:0）的相机，木框是视口，就是也就是相机的镜头，画布就是你要展现的平面。

 

 

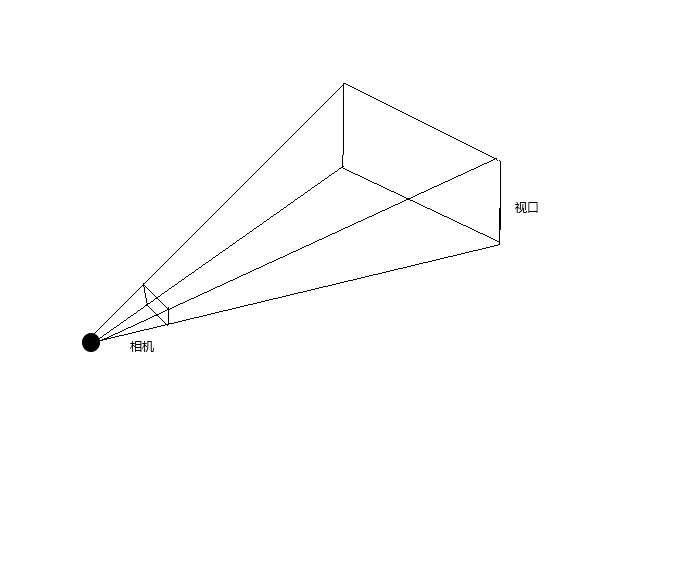
因为在例子中，木框和画布都存在渔网格，保证了每个格子的大小和位置，数量是一样的。也就是说木框和画布的宽高是存在一定比例。

 

因为我们是在画布上每一个网格绘制我们在木框上同一个网格看到的内容，也就是我们要确定木框上网格位置，换句说 画布的网格是确认的，我们反推木框上的网格位置。

换到计算机，我们最终是要在图片上，也就是画布上去显示，确定图片或者画布的坐标是简单的。

正常来说，现实中的 我们能看到东西是因为物体反射的光进入了眼中。不过我们为了简单，反过来计算，我们的相机主动发出光去看。

这里面还有个非常重要点的，就是3D坐标，相当于2D坐标多了一个Z轴，我们相机是看向+Z轴的，我们任何东西都是存在于3D空间的（相机，视口，物体）。当然，画布不是哦。

 

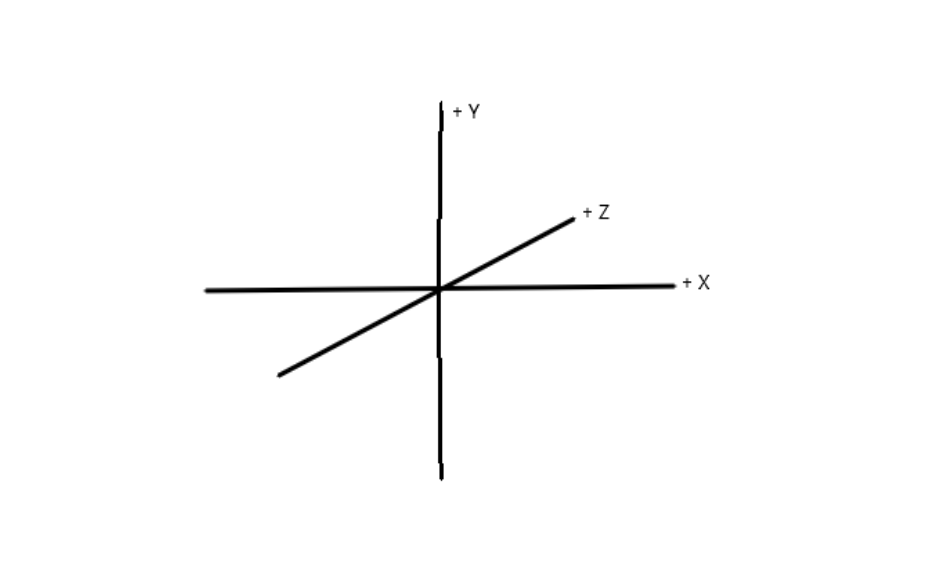
简单来说我们用Vw,Vh来定义视口的宽高，Cw，Ch定义画布的宽高，

并定义画布到视口的坐标为

Vx=Vw/Cw*Cx

Vy=Vh/Ch*Cy

目前来说这个视口是一个2D的，只不过是嵌套在3D空间而已，即便是2D的，这个视口上的每一个点都和相机存在一个距离，那么我们定义这个距离为d，使的每一个点的Zd=d。

这样，我们就得到画布的每一个点（Cx,Cy）都可以得到视口上的对应的位置（Vx,Vy,Vd）。

 

追踪射线

我们是从相机发出射线经过视口看物体。

而射线碰到什么决定了我们看到了什么。

其实射线就是向量，相机的位置是原点，通过视口时，向量有了角度，当向量不断前进，直到碰到的物体。此刻我们就知道可以绘制什么。

至于绘制什么，可以理解为向量就是我们的视线，看到了什么就绘制什么。

实际上每个向量的就是像素的显示，和圆碰到了显示的就是向量与圆的相交的点的颜色，没碰到就是背景色。

点 P=O+tD

O是原点，D是（空间内的某一点的坐标V，V-O），t是前进的数量。tD就是个向量数乘，D可以理解为方向。

那么这就是求t，t值决定了射线是否碰到了射线。

因为我们是绘制了球体，也就是圆与直线的相交。但是3D空间中的圆是球，可以理解为半径到圆心在各个方向上的合集，圆心到球体的边缘的距离就是半径。

 

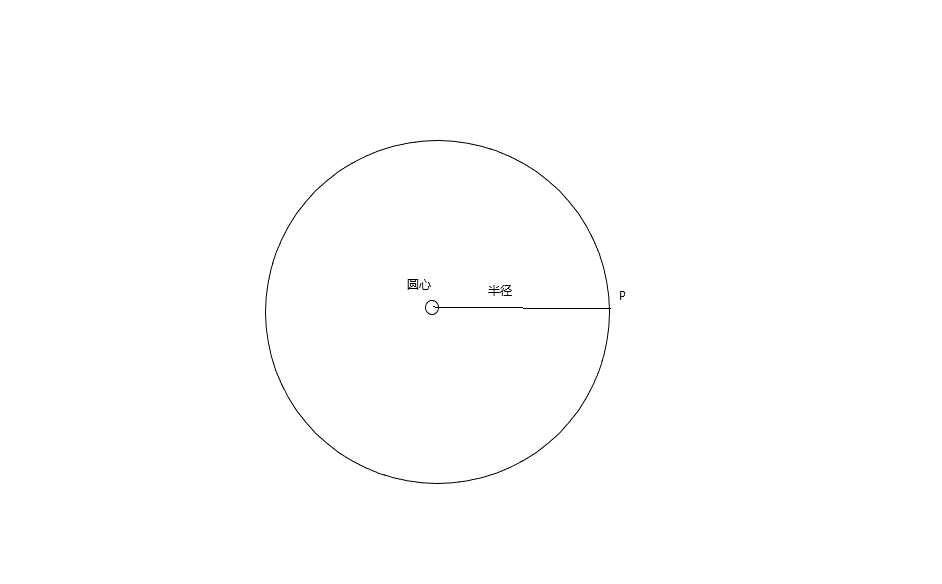
半径就是r,圆心是C

r² =(P-C ) dot (P-C)

r² =根号下（P-C）的点积。

我们将P替换成O-tD,得到

(O+tD-C)dot(O+tD-C)=r² ，我们利用交换律替换成（O-C+tD）,O-C是一个向量，我可以用OC代替。最终是

(OC+tD) dot (OC+tD)=r² ,因为是点积，我们可以利用分配律展开第一个括号

OC dot（OC+tD）+ tD dot (OC+tD)=r² 即 为：

 OC dot OC+ OC dot tD+ tD dot OC +tD dot tD=r²

 

(OC dot OC)+2(OC Dot tD)+(tD dot tD)=r2,因为点乘可以引用结合律，所以

2OC dot tD=2(t(OC dot D))=2t(OC dot D)

(tD dot tD)=t*(D) dot t*(D)=t*(D dot t*D)=t*(t*(D dot D ))=t^2(D dot D)

最终是

(OC dot OC)+2t(OC dot D)+t^2(D dot D)=r^2。

我们调换下位置t^2(D dot D)+2t(OC dot D)+(OC dot OC)-r^2=0

使用

a=(D dot D)

b=2(OC dot D)

c =(OC dot OC)-r^2

就是  at^2+bt+c=0,一次二元方程，所以我们能解出t，

也就是 (-b±根号下（b^2-4ac))/2a,当然t有几个不同情况

可能有解，一个解，两个解。如下图

 

 

代码

基本条件差不多了，我们来开始实践吧。

由于我们是用WPF，所以我们注意一下我们的坐标系转换，也就是3D坐标系到屏幕坐标系。

屏幕坐标系是以左上角为起点的，我们算的时候是以3D坐标系为基准，当我们真正输出到屏幕或者绘制时要注意转换。

剩下就是定义球的方法，要有半径，有3D坐标的中心，填充颜色

简单模型

　　　　class sharp
        {
            public Vector3D center
            {
                get; set;
            }
            public double radius { get; set; } = 1;
            public Color color
            {
                get; set;
            }
        }

我们定义三个

 　　　　  List<sharp> sharplist = new List<sharp>
        {
        new sharp() { center = new Vector3D(0, -1, 3), color = Colors.Red },
        new sharp() { center = new Vector3D(2, 0, 4),  color = Colors.Blue },
        new sharp() { center = new Vector3D(-2, 0, 4), color = Colors.Green }
        };

 

定义 一元二次方程的解

　　　　 /// <summary>
        /// 求解一元二次
        /// </summary>
        /// <param name="origin">起点</param>
        /// <param name="dline">向量</param>
        /// <param name="sharp">球体</param>
        /// <returns></returns>
        Point IntersectRayShere(Vector3D origin, Vector3D dline, sharp sharp)
        {
            //半径
           　　　　 double r = sharp.radius;
            //起点到圆心
           　　　　 var co = origin - sharp.center;
            
            var a = Vector3D.DotProduct(dline, dline);

            var b = 2 * Vector3D.DotProduct(co, dline);

            var c = Vector3D.DotProduct(co, co) - r * r;

            var discrinimant = b * b - 4 * a * c;

            if (discrinimant < 0)
            {
                return new Point();
            }
            var t1 = (-b + Math.Sqrt(discrinimant)) / (2 * a);
            var t2 = (-b - Math.Sqrt(discrinimant)) / (2 * a);
            //偷懒
            　　　　return new Point(t1, t2);
        }

 光线追踪

 

    /// <summary>
        /// 光线追踪
        /// </summary>
        /// <param name="origin">起点</param>
        /// <param name="dline">方向</param>
        /// <param name="min">射线最小值</param>
        /// <param name="max">射线最大值</param>
        Color tracrray(Vector3D origin, Vector3D dline, double min, double max)
        {
            double closet = double.PositiveInfinity;
            sharp claset_sharp = null;
            //遍历模型
            foreach (var item in sharplist)
            {
                //求解是否与圆相交
                var gp = IntersectRayShere(origin, dline, item);
                //小于判断
                if (gp.X >= min && gp.X <= max && gp.X < closet)
                {
                    closet = gp.X;
                    claset_sharp = item;
                }
                if (gp.Y >= min && gp.Y <= max && gp.Y < closet)
                {
                    closet = gp.Y;
                    claset_sharp = item;
                }
            }
            //不存在返回空白值
            if (claset_sharp == null)
            {
                return Colors.White;
            }
            //
            return claset_sharp.color;
        }

 

 

 

开始扫描绘制

  　　　　　　WriteableBitmap.Lock();
            //画布开始
           　　　　 for (double x = 0 - cw / 2; x < cw / 2; x++)
            {
                for (double y = 0 - ch / 2; y < ch / 2; y++)
                {
                    //画布到视口
                    var D = canvastoviewport(new Point(x, y));
                    //获取像素颜色
                    var color = tracrray(new Vector3D(), D, 1, double.PositiveInfinity);
                    //坐标系转换
                    var p = MidPoint(new Point(x, y));
                    //定义颜色BGRA
                    byte[] colorData = { color.B, color.G, color.R, color.A };
                    //跨距
                    int stride = (WriteableBitmap.PixelWidth * WriteableBitmap.Format.BitsPerPixel) / 8;
                    //绘制
                    WriteableBitmap.WritePixels(new Int32Rect((int)p.X, (int)p.Y, 1, 1), colorData, stride, 0);
                }
            }
            WriteableBitmap.Unlock();

 于是我们得到

 

 

 

具体代码参考计算机图形学入门_3D渲染指南: 由C#作为编程语言，WPF作为输出。 计算机图形学入门3D渲染指南 - Gitee.com