WPF 基于五点线性平滑曲线算法

线性算法是基于最小二乘法所计算的平滑算法，

具体可以参考这篇博客几个简单的数据点平滑处理算法_Ivan 的专栏-CSDN博客_数据平滑处理

其他的算法原文解释是：

算法的原理很简单，以五点三次平滑为例。取相邻的5个数据点，可以拟合出一条3次曲线来，然后用3次曲线上相应的位置的数据值作为滤波后结果。简单的说就是 Savitzky-Golay 滤波器 。

只不过Savitzky-Golay 滤波器并不特殊考虑边界的几个数据点，而这个算法还特意把边上的几个点的数据拟合结果给推导了出来。

 

我没找到具体原公式...这一点很是遗憾，也不知道到底根据什么算的系数.

代码不是C#的，但是很好改成C#。

我觉得线性的代码就很不错了，速度也很快。

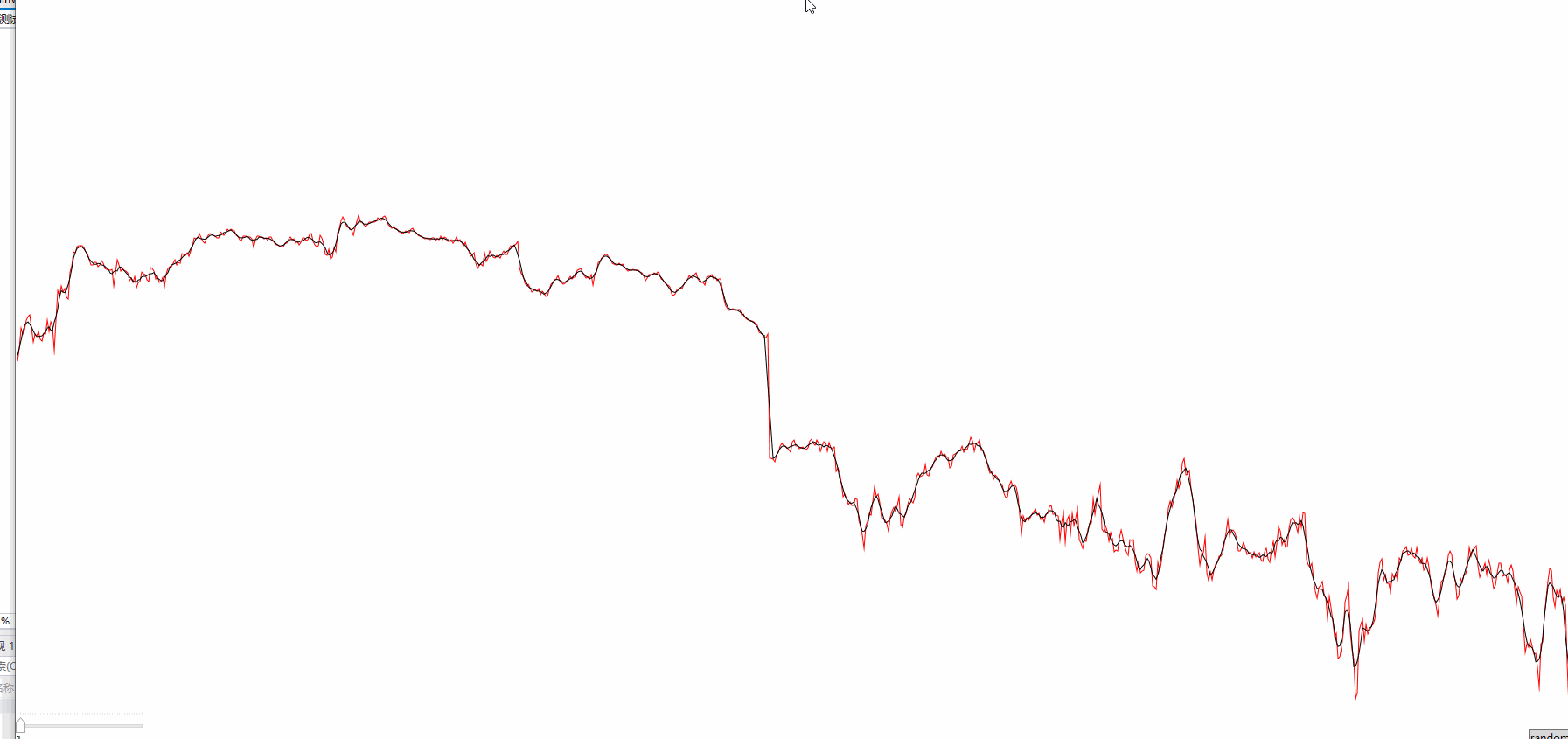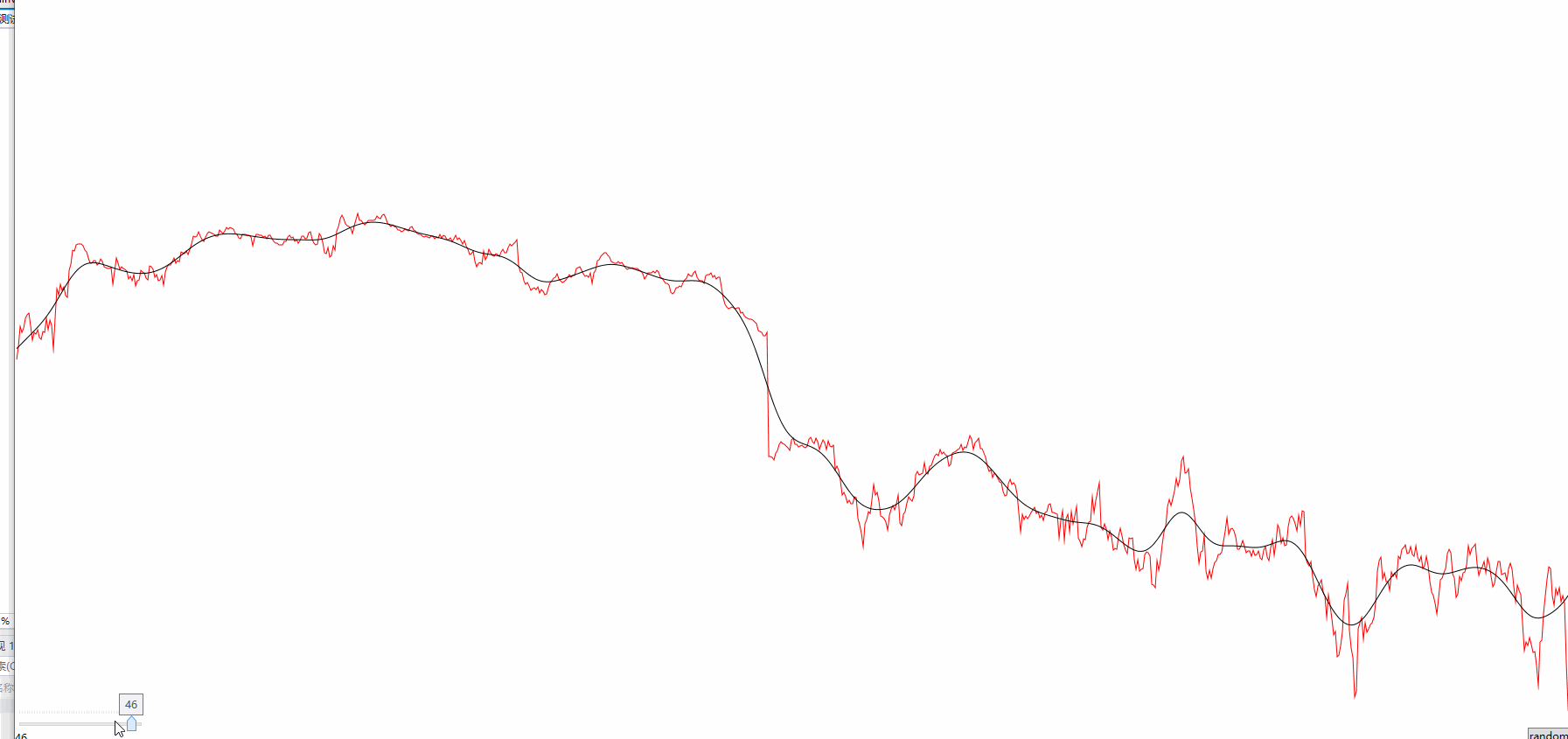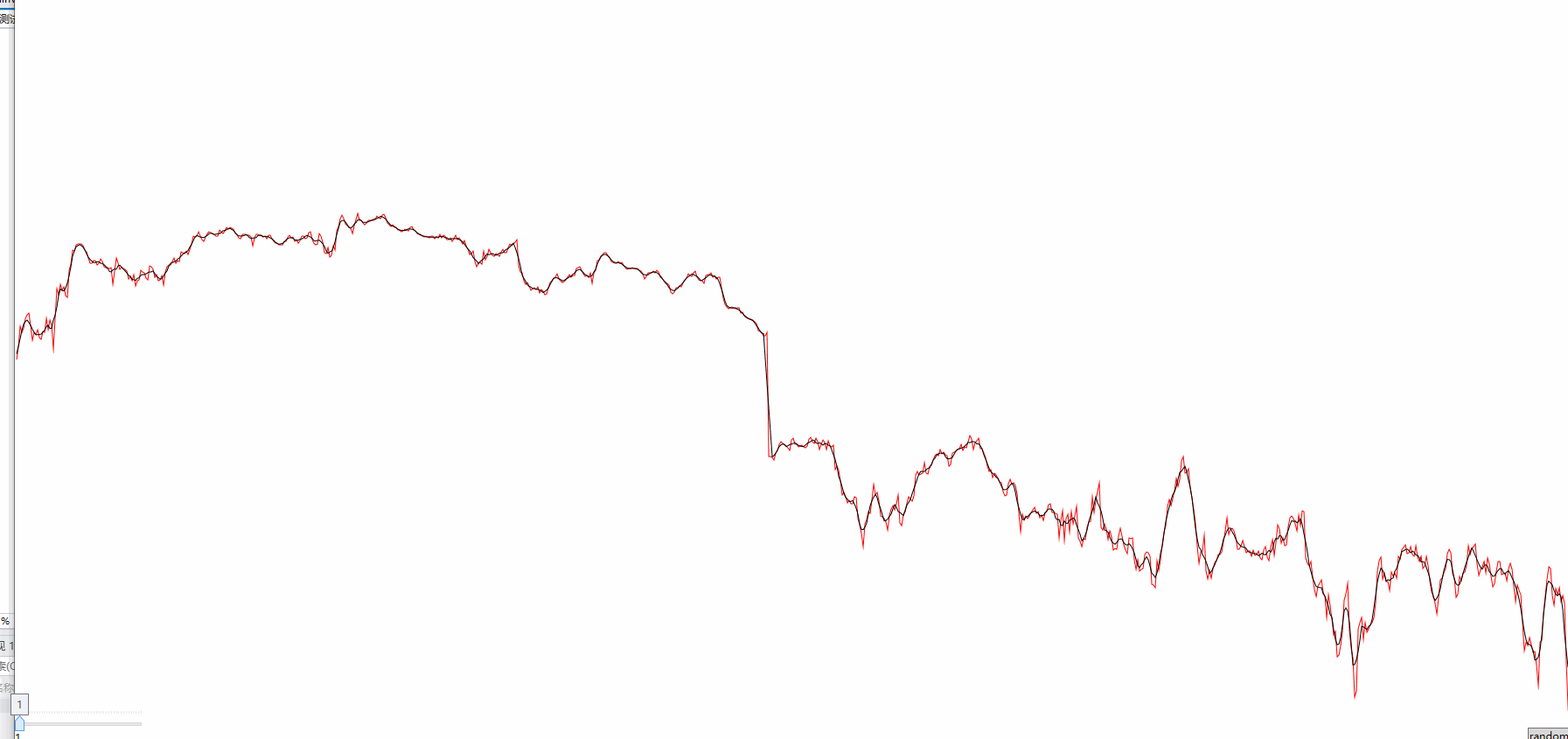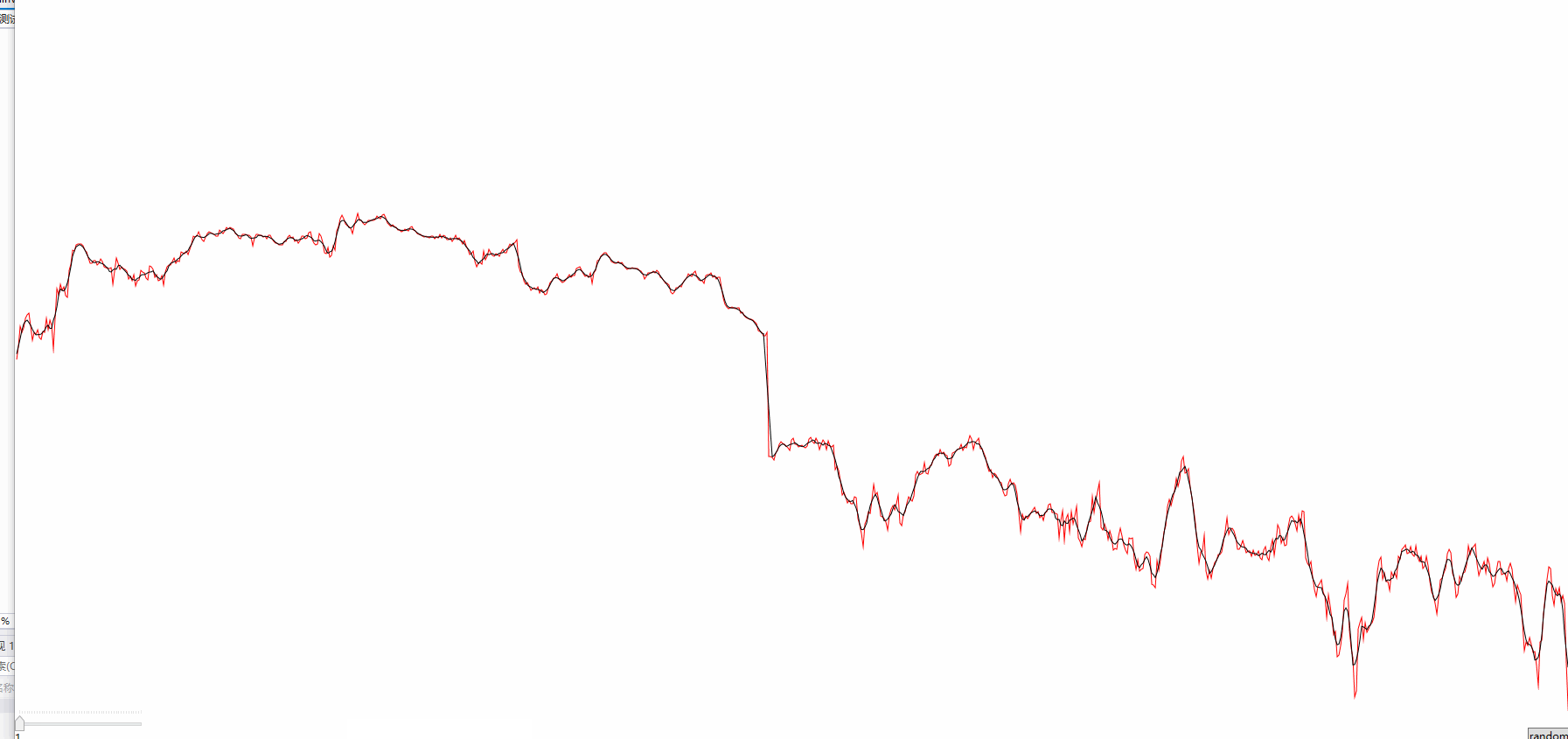
迭代的次数最好是小于20次，不然就趋向于直线了，这个算法也许不一定适用所有的情况，时间序列应该是没多大问题的。

 

 

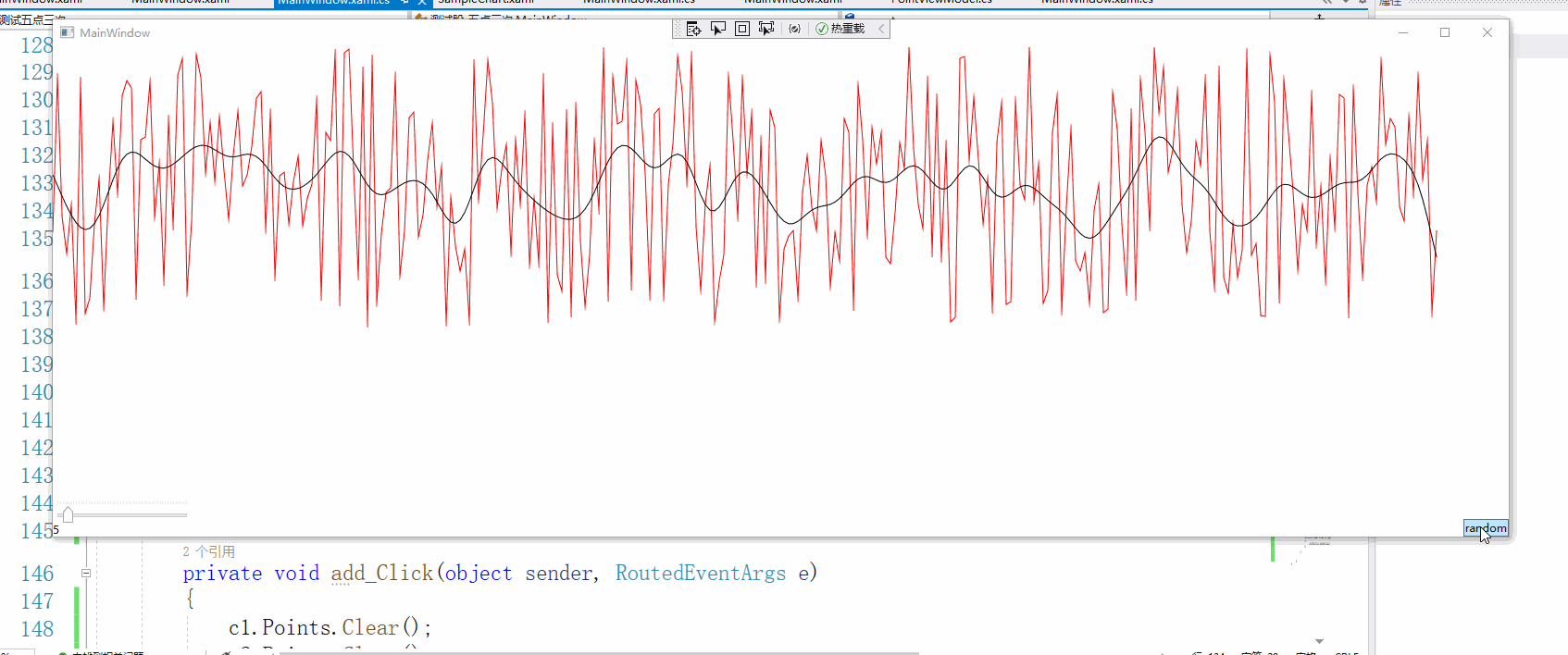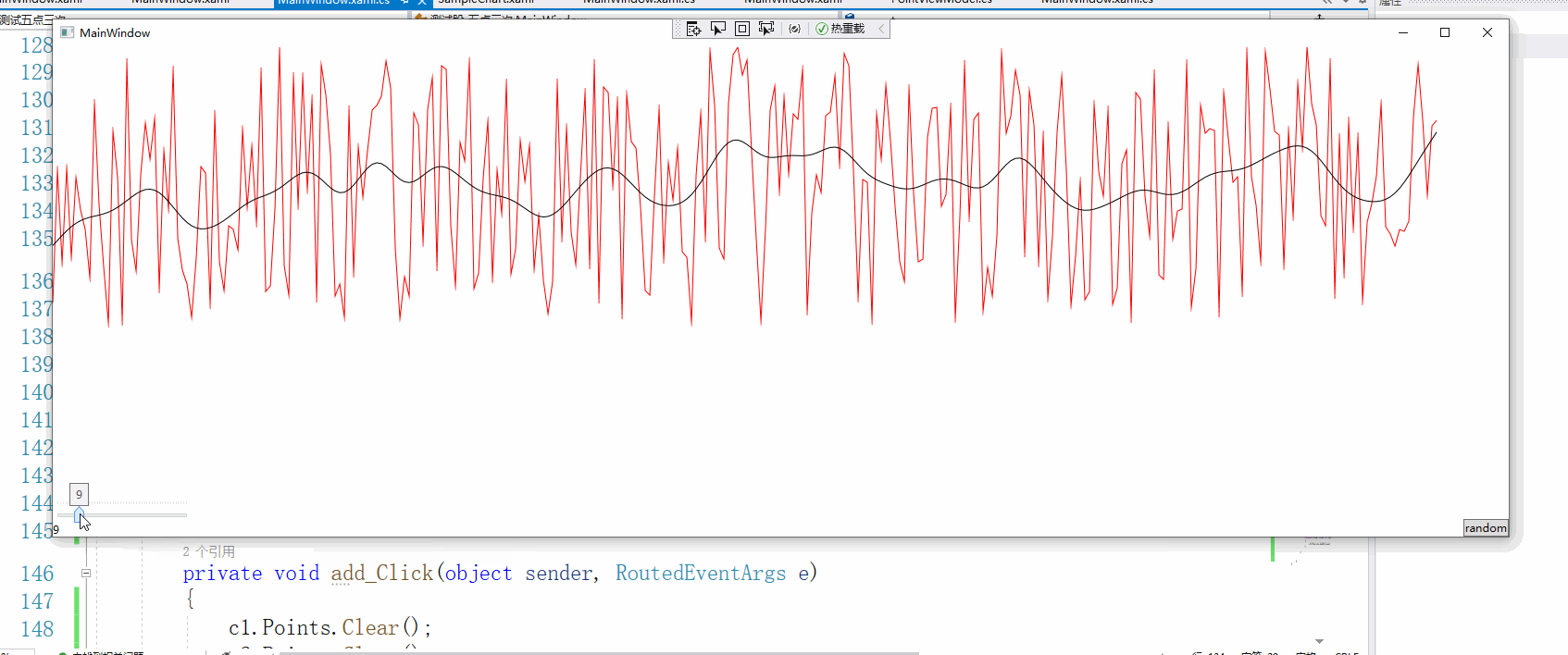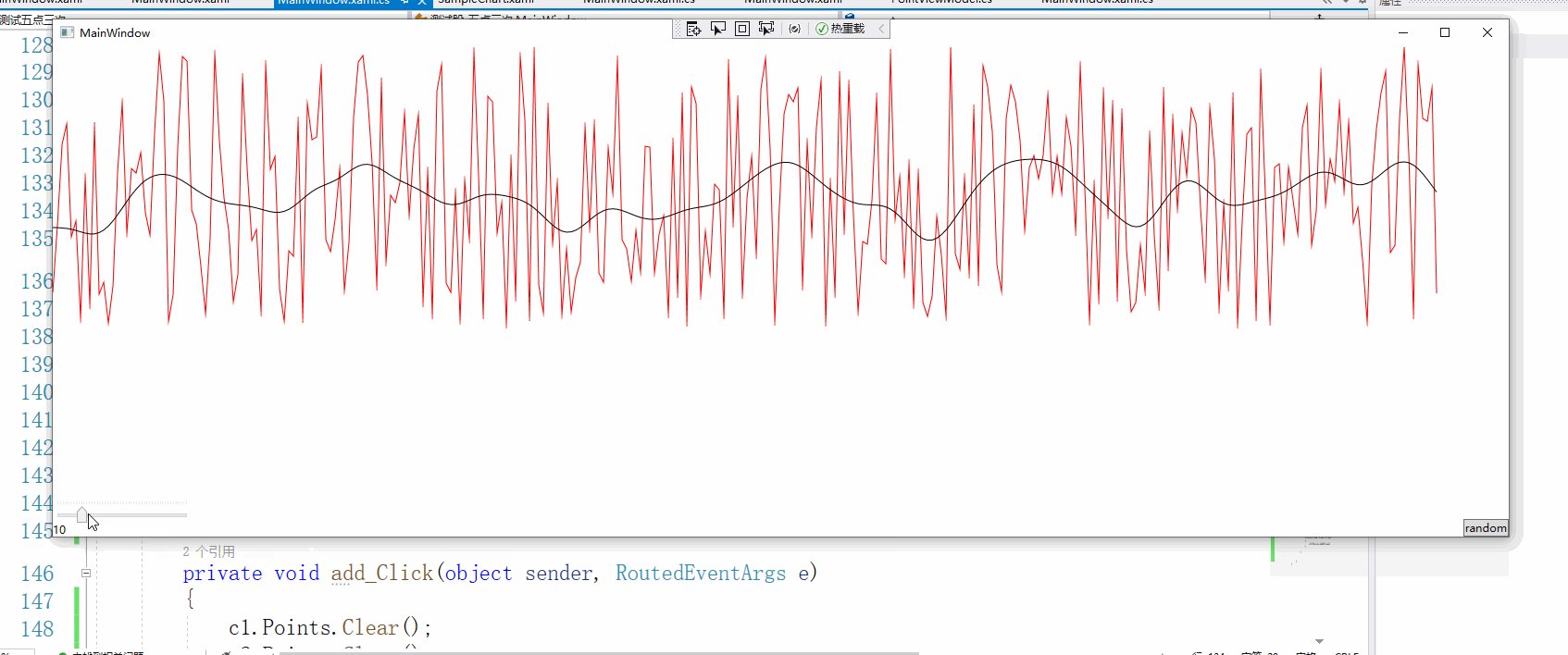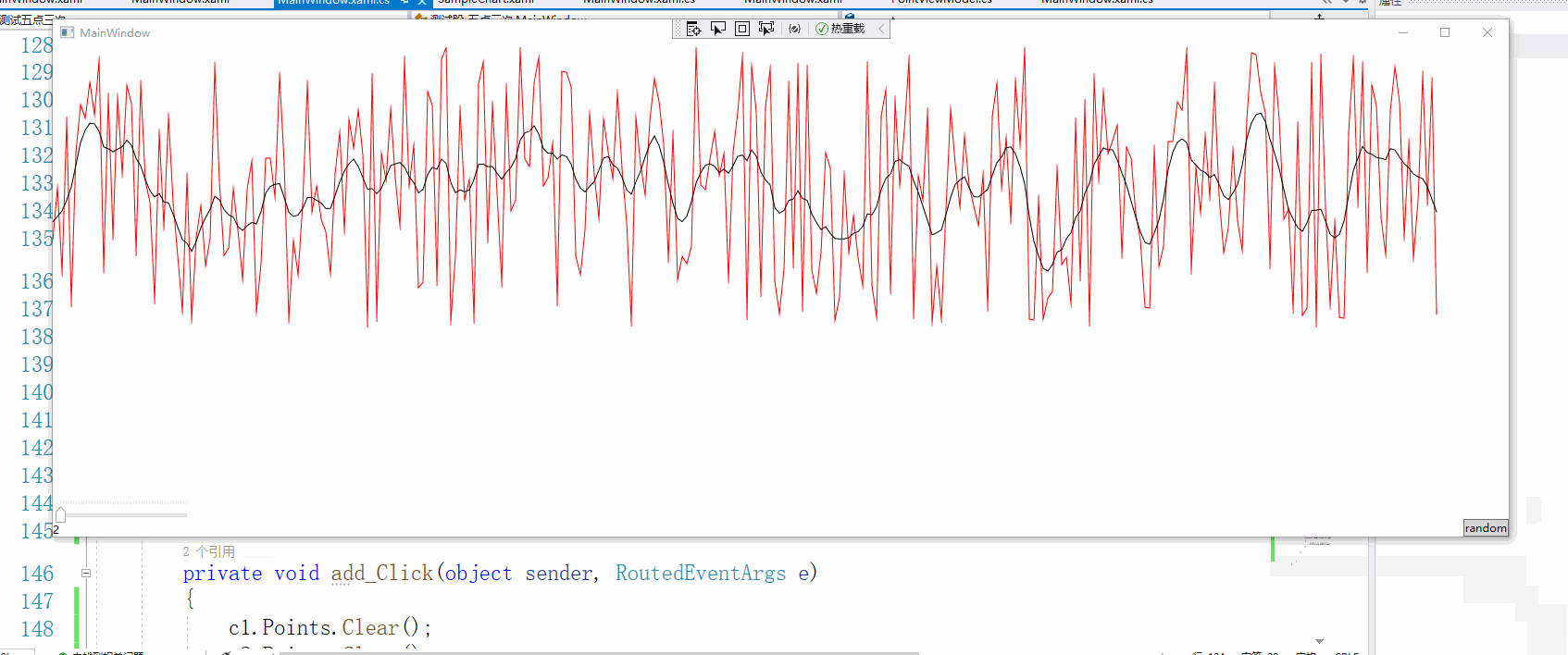
这个数据是我截取某个股票的数据，数据点1200个，看得出平滑的效果还是不错的

 

 

 

修改的代码

   private List<Point> linearSmooth5(List<Point> Data)
        {

            List<Point> restult = new List<Point>();
            var count = Data.Count;
            if (count <= 5)
            {
                for (int i = 0; i <= count - 1; i++)
                {

                    restult.Add(Data[i]);
                }
            }
            else
            {

                double y = (3.0 * Data[0].Y + 2.0 * Data[1].Y + Data[2].Y - Data[4].Y) / 5.0;
                restult.Add(new Point(Data[0].X, y));
                y = (4.0 * Data[0].Y + 3.0 * Data[1].Y + 2 * Data[2].Y + Data[3].Y) / 10.0;
                restult.Add(new Point(Data[1].X, y));
                for (int i = 2; i <= count - 3; i++)
                {
                    y = (Data[i - 2].Y + Data[i - 1].Y + Data[i].Y + Data[i + 1].Y + Data[i + 2].Y) / 5.0;
                    restult.Add(new Point(Data[i].X, y));
                }
                y = (4.0 * Data[count - 1].Y + 3.0 * Data[count - 2].Y + 2 * Data[count - 3].Y + Data[count - 4].Y) / 10.0;
                restult.Add(new Point(Data[count - 2].X, y));
                y = (3.0 * Data[count - 1].Y + 2.0 * Data[count - 2].Y + Data[count - 3].Y - Data[count - 5].Y) / 5.0;
                restult.Add(new Point(Data[count - 1].X, y));
            }
            return restult;
        }