WPF 拉格朗日插值法简单实现

学习学习文化，提升自己

拉格朗日插值法，解释起来差不多就是，【有很多点，我不知道构造这些点的具体函数，但是我可以尝试在每个点的时让其他点的纵坐标都为零，这个点为纵坐标为1，此时得到一个点的函数，后续每个点重复操作，最后相加即可】

知乎这篇说明就很不错

 

先上截图

 

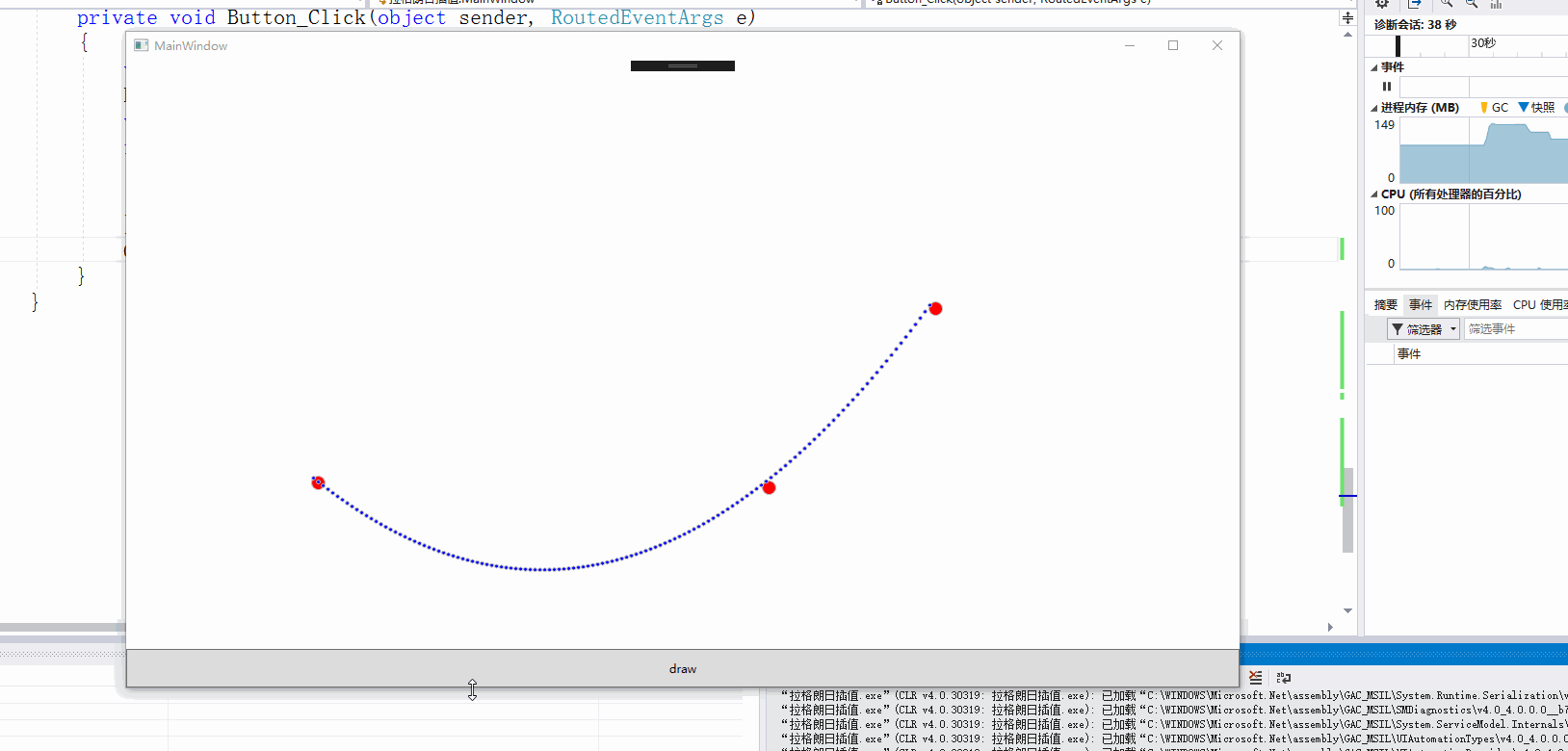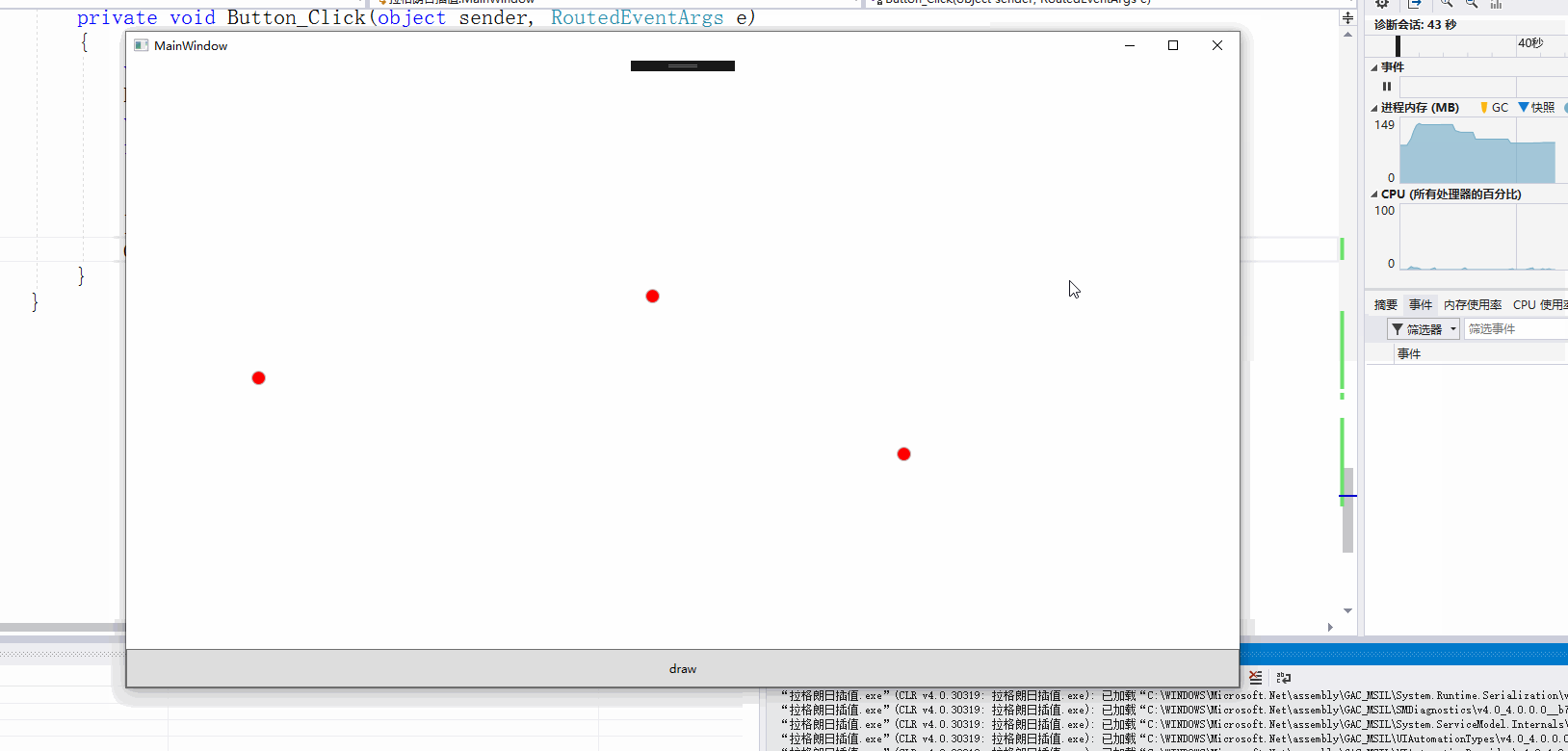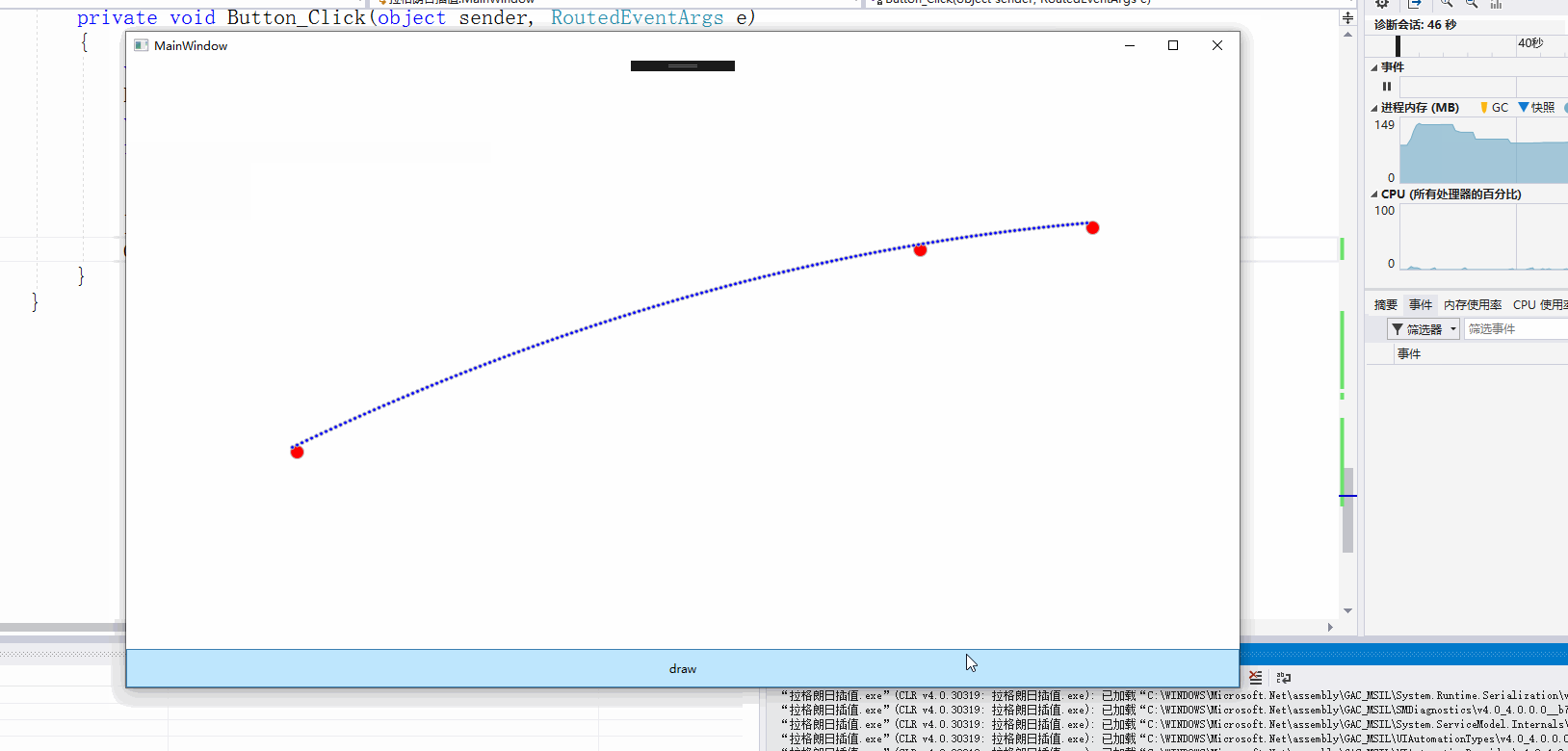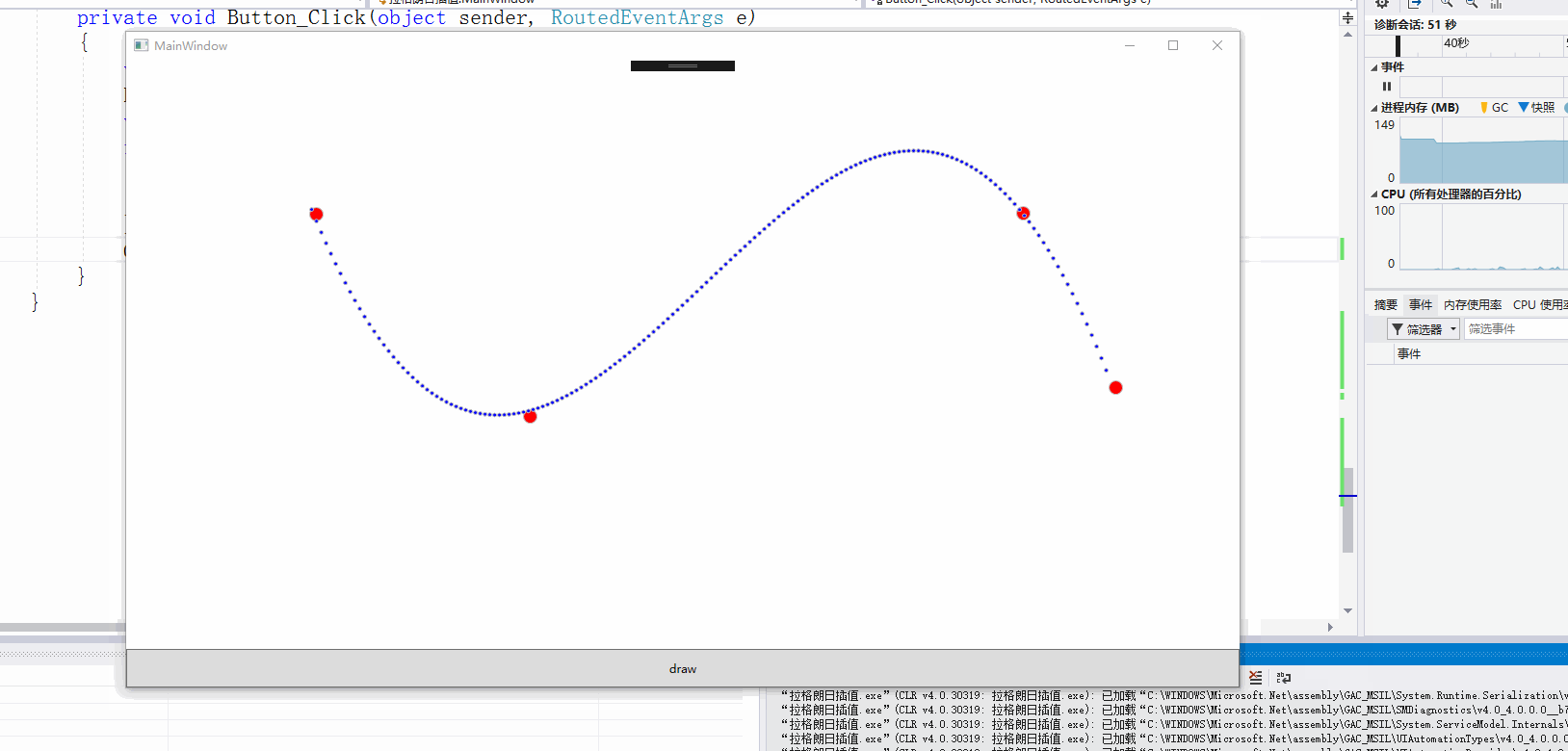
xaml的具体代码：主要是对canvas的绘图绑定

 <Grid >
        <Grid.RowDefinitions>
            <RowDefinition Height="*"/>
            <RowDefinition Height="auto"/>
        </Grid.RowDefinitions>
        <ItemsControl Background="White" x:Name="T1" ItemsSource="{Binding    EP }" PreviewMouseLeftButtonUp="T1_PreviewMouseLeftButtonUp">
            <ItemsControl.ItemsPanel>
                <ItemsPanelTemplate>
                    <Canvas   />
                </ItemsPanelTemplate>
            </ItemsControl.ItemsPanel>
            <ItemsControl.ItemTemplate>
                <DataTemplate>
                    <ContentControl Content="{Binding UI}"/>
                </DataTemplate>
            </ItemsControl.ItemTemplate>
            <ItemsControl.ItemContainerStyle>
                <Style >
                    <Setter Property="Canvas.Top" Value="{Binding Y}"/>
                    <Setter Property="Canvas.Left" Value="{Binding X}"/>
                </Style>
            </ItemsControl.ItemContainerStyle>
        </ItemsControl>
        <Button Height="40" Grid.Row="1" Click="Button_Click" Content="draw"/>
    </Grid>

 

后台代码

namespace 拉格朗日插值
{
    public class EPS
    {
        private double _x;

        public double X
        {
            get { return _x; }
            set { _x = value; }
        }

        private double _y;

        public double Y
        {
            get { return _y; }
            set { _y = value; }
        }

        private Ellipse ellipse;

        public Ellipse UI
        {
            get { return ellipse; }
            set { ellipse = value; }
        }
        public EPS(Point point,bool b=true)
        {
            UI = new Ellipse
            {
                Stroke = new SolidColorBrush(Colors.Silver),
                Fill = new SolidColorBrush(b ? Colors.Red : Colors.Blue),
                Height = b ? 15 : 5,
                Width = b ? 15 : 5
            };
            Y = point.Y;
            X = point.X;
        }
        public EPS()
        {

        }
    }
    /// <summary>
    /// MainWindow.xaml 的交互逻辑
    /// </summary>
    public partial class MainWindow : Window
    {
        public ObservableCollection<EPS> EP { get; set; }
        public MainWindow()
        {
            InitializeComponent();
            EP = new ObservableCollection<EPS>();
            DataContext = this;
        }

        private void T1_PreviewMouseLeftButtonUp(object sender, MouseButtonEventArgs e)
        {
            if (CanDraw)
            {
                EP.Clear();
                CanDraw = false;
            }
            EP.Add(new EPS(e.GetPosition(T1)));
            //两点基画法
            //if (EP.Count > 3)
            //{
            //    EP.Clear();
                
            //}
            //if (EP.Count == 2)
            //{
            //    for (double i = EP[0].X; i < EP[1].X; i+=1)
            //    {
            //        EP.Add(new EPS(new Point(i,Towpoint(i)),false));
            //    }
            //}
           
        }
        double Towpoint(double x)
        {
            var b=
                (EP[0].Y * ((x - EP[1].X) /( EP[0].X - EP[1].X)) )
                + 
                (EP[1].Y * ((x - EP[0].X) /( EP[1].X - EP[0].X)));
            return b;
        }
        double MultiPoint(List<EPS> Points,double x)
        {
            var k = (from item in Points
                    let l1 = item.Y
                    * (Points.Where(c => c != item).Select(p => x - p.X).Aggregate((a, b) => a * b))
                    / (Points.Where(c => c != item).Select(p => item.X - p.X).Aggregate((a, b) => a * b))
                    select l1).Sum();
                return k;
        }
        bool CanDraw;
        private void Button_Click(object sender, RoutedEventArgs e)
        {
            var k = new EPS[EP.Count];
            EP.CopyTo(k, 0);
            var items = k.ToList();
            for (double  i = EP[0].X; i < items.Last().X; i+=5)
            {
                  EP.Add(new EPS(new Point(i, MultiPoint(items, i)), false));
            }
            CanDraw = true;
        }
    }
}

主要说说关于多点的linq写法

拉格朗日插值法的算法通俗而言也就是

点的纵坐标值乘与未知点的横坐标减去其他点的横坐标的乘积并除以这个点的横坐标减去其他点的横坐标的乘积，最后相加即可

所以我们首先得某个点，紧接着过滤掉自身，并开始计算分子的未知点的x减去其他点的X坐标最后使用累加函数相乘即可，当然还要重复一次求分母，并将未知点的X替换为这个点的X坐标

最后相加即可