在字节海洋中沉浮
前言
在我所在的校队中，很多颇有名望的前辈都喜欢记录自己在比赛期间的所见所闻。而且，受到了《绝区零》中格莉丝的“新型空洞内特殊作业用工业机器开发日志”的激励后，我希望找到一种可持续的记录自己成长的方式。无论是信息学竞赛方面，抑或是文化课方面。
所以，从今天起，我决定，尝试以一篇文章的方式，记录我的历程。
以上，\(2024\) 年 \(8\) 月 \(1\) 日，记录开始。
2024/8/1 - 介绍
我，一个在校队中不上不下的奥信选手，一个在年级中不上不下的准初三学生。对语文、政治、历史等死记硬背的科目十分厌烦，对数学、英语、物理、化学等重在思考的科目喜好有加。
好不容易在期末考试前初步摸出了政治论述题的答题格式，在真正考试的时候又没选对材料。
在前天的 Codeforces 教育场中出乎意料地拿到了不错的成绩，可以见这篇文章。作者就是我的账号。
为什么这样说呢？因为，对我来说，在一场正常的 CF Div.2 比赛中，能解决 \(2\) 题是正常水平，解决 \(3\) 题是运气好，而解决 \(4\) 道或以上的题就是撞大运了。
我还在 CodeChef 中参加比赛，因为这个网站经常出数学相关的题目，而且这里的 Div.1 约等于 CF 的 Div.2。
昨天我就在这个网站参加了一场比赛，在 \(6\) 题中解决了 \(3\) 题。
AtCoder 也不错。这个网站出的题目几乎全部是精妙的思维题，能让你的大脑高速旋转。
我暑假作业还没写完。结果，我很快就要去学校集训了。
在那时，我能碰到什么样的题呢？
Phase \(1\) - 现役
2024/8/5 - 启程/NOIP 比赛 \(1\)
基本配置报告：宿舍没有蚊子，存在极少量蟑螂，洗衣服务禁用。
勉强还行。
今天比赛的题目来自牛客。
四道题的考点分别为数学，前缀和/并查集/启发式合并，树上分块，缩点。
分值：\(100+100+45+0=245\)。
排在校队所在分部第 \(3\) 名，还算不错。
笑点解析其一：学校电脑 Windows \(7\)，无法支持 vscode 最新版本，遂改用 vim。
2024/8/6 - NOIP 比赛 \(2\)
洗衣服务能用了。
今天四道题的考点分别为数学，数学，数学以及分块。
以下是我打完比赛后的暴论：
首先，我***，T3 的输入数据绝对有问题。
得分情况：\(100+75+90+25=290\)。
T1，看到题目认为有显然的贪心策略，正解也确实如此，但是测大样例后认为最优方案是全选就一直认为方案周了，然而并没有。
T2，第一眼认为不可做，但是后来发现可以使用前缀和和后缀和算出每个位置的固定贡献，万万没想到被题目骗了，上了个线段树，比赛结束之后才发现不用线段树，换成前缀和就过了，甚至是目前用时最少的代码。
T3，首先我要*出题人，第一眼觉得不可做，后来遵照伟大先师 cyk 的指示睡了半个小时，然后发现***还是拆贡献，然后用 \(20\) 分钟打了出来。然后，快读 \(90\) 分，scanf \(100\) 分。我***
T4，没有任何思路，写了个循环展开尝试多捞点分，最终只额外捞到 \(5\) 分。
总结：造数据的人我***
2024/8/7 - ICPC 比赛 \(1\)
众所周知，我校的教练与杭电大有深入交流，而我们校内举办的多场 ICPC 比赛直接使用了杭电大校赛的题目。本场比赛采用的题目为“\(2024\)‘钉耙编程’中国大学生算法设计超级联赛 \(1\)”。
AC 编号：ABEHL。
本场比赛采用了一种十分创新的组队方式，名为“强制组队”，据教练解释，其意思是根据前两天的 NOIP 模拟赛进行平均的分组。
我所在的队名为“蒸鱼王”，其中每个字采用了每个队员的姓的谐音。
“蒸”负责 EL，“鱼”负责 AB，“王”负责 H。可以说，“王”打响了第一枪，“鱼”完成了难度中等的模拟题，“蒸”为我队的排名提供了保障。
“蒸”所负责的两道题均为难度极高的数学题，原因是“蒸”在编程领域专精数学。
2024/8/8 - NOIP 比赛 \(3\)
自闭了。
在一道题上卡了 \(2\) 个小时。
不想写。
2024/8/9 - NOIP 比赛 \(4\)
还是不想写。在简单的题目上绕到了死角里面，还没有出来。
再次自闭。
总结如下。
分值：\(80+0+70+0=150\)。
T1，调试过程贯穿整场比赛，赛时非常不幸地没有意识到一个节点最多访问两次，然后还坚定不移地认为自己的思路没有问题，于是在比赛结束前半个小时才写出 \(80\) 分的代码。
T2，不同于上一个周期诈骗性质的期望题，这次的题面已经足够让我绝望了。所以并没有写这道题。
T3，通过在之前 CF 比赛中积累的打表找规律经验，成功猜推出了这道博弈论的 \(O(V)\) 递推解法，拿到 \(70\) 分。正解花了半个多小时找，还发现了黄金分割率，结果还是找不出来，于是就没有再看。
T4，一眼看出选的一定是叶子，然而没有什么用，正解想不出来，暴力也不太想打。
总结：上个周期第一，这个周期倒数，我真是个莫得实力的选手。
2024/8/10 - ICPC 比赛 \(2\)
果不其然，教练再次选择了杭电的 \(2024\) 钉耙编程赛 \(2\)。
队名为“马学张网捕鱼”，同样继承了使用队友姓名命名的优良传统。
以下直接以 HDU 题号进行讲述。
AC 顺序：GJFKACH。
G，即 HDU7451，URL 划分。本题为本场比赛第一个签到题，由“鱼”负责，因为输入处理失误而吃了一发罚时，然而并不影响我们拿到首 A。直接按照题目模拟即可，注意细节。
#include<iostream>
#include<string>
using namespace std;
const int N=1e5+10;
string s,t;
int tag;
void run(){
cin>>s;
t="";
tag=0;
for(auto& i:s)
{
if(i==':' or i=='/')
{
if((tag<2 or t.find('=')!=t.npos) and t.size())cout<<t<<'\n',tag++;
t="";
continue;
}
t+=i;
}
// if(t.size())cout<<t<<'\n';
}
int main(){
int T=1;
scanf("%d",&T);
while(T--)run();
}
J，即 HDU7454，女神的睿智。本场比赛第二道签到题，同样由“鱼”负责，按照题目模拟即可。
#include<iostream>
#include<string>
#include<map>
using namespace std;
const int N=8;
map<char,int> mp;
string s,t;
void run(){
cin>>s;
mp.clear();
for(auto& i:s)mp[i]++;
if(mp[s[0]]==mp[s[4]] and s[0]!=s[4])puts("N");
else if(mp[s[0]]>mp[s[4]])putchar(s[0]),putchar('\n');
else putchar(s[4]),putchar('\n');
}
int main(){
int T=1;
scanf("%d",&T);
while(T--)run();
}
F，即 HDU7450，传奇勇士小凯。一道相对简单的期望，由“马”负责。
#include <cstdio>
#include <vector>
#define int long long
using namespace std;
int t,n,p[100007];
vector<int> g[100007];
int gcd(int a,int b){
return b==0?a:gcd(b,a%b);
}
struct frac{
int x,y;
bool operator < (frac b){
return x*b.y<b.x*y;
}
frac operator + (frac b){
int Y=y*b.y;
int X=x*b.y+b.x*y;
int g=gcd(X,Y);
if(g!=0) X/=g,Y/=g;
return (frac){X,Y};
}
frac(){
x=0,y=1;
}
frac(int a,int b){
int g=gcd(a,b);
//printf("%d\n",g);
if(g!=0) a/=g,b/=g;
x=a,y=b;
}
}dp[100007];
void dfs(int u,int fa){
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(v==fa) continue;
dfs(v,u);
if(dp[u]<dp[v]) dp[u]=dp[v];
}
dp[u]=dp[u]+frac(15,p[u]);
}
signed main(){
scanf("%lld",&t);
while(t--){
scanf("%lld",&n);
for(int i=1;i<=n;i++) g[i].clear(),dp[i]=frac(0,1);
for(int i=1,x,y;i<n;i++){
scanf("%lld%lld",&x,&y);
g[x].push_back(y);
g[y].push_back(x);
}
for(int i=1;i<=n;i++){
scanf("%lld",&p[i]);
}
dfs(1,0);
printf("%lld/%lld\n",dp[1].x,dp[1].y);
}
return 0;
}
K，即 HDU7455，在 A 里面找有 C 的 B。本题由于“鱼”的实现不善导致三发罚时后转交给“张”负责，随后一次过。解法为将 AC 自动机和哈希结合。
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
int n,cnt,TT;
int ans[N],pos[N],in[N],Ne[N];
string s,T,C,Q[N];
struct node{
int son[30];
int end;
int fail;
int ans;
}t[N];
vector<int> Ans;
void insert(string x,int id){
int u = 0;
for(int i = 0;i<(int)x.size();i++){
int v = x[i]-'a'+1;
if(t[u].son[v] == 0)
t[u].son[v] = ++cnt;
u = t[u].son[v];
}
if(!t[u].end) t[u].end = id;
pos[id] = t[u].end;
}
void getfail(){
queue<int> q;
for(int i = 1;i<=26;i++)
if(t[0].son[i])
q.push(t[0].son[i]);
while(q.size()){
int now = q.front();
q.pop();
for(int i = 1;i<=26;i++){
if(t[now].son[i]){
t[t[now].son[i]].fail = t[t[now].fail].son[i];
in[t[t[now].son[i]].fail]++;
q.push(t[now].son[i]);
}
else t[now].son[i] = t[t[now].fail].son[i];
}
}
}
void query(string x){
int u = 0;
for(int i = 0;i<(int)x.size();i++){
int v = x[i]-'a'+1;
u = t[u].son[v];
t[u].ans++;
}
}
void topo(){
queue<int> q;
for(int i = 1;i<=cnt;i++)
if(!in[i]) q.push(i);
while(q.size()){
int u = q.front();
q.pop(); ans[t[u].end] = t[u].ans;
int v = t[u].fail;
in[v]--;
t[v].ans+=t[u].ans;
if(!in[v]) q.push(v);
}
}
void getnext(string p){
Ne[0] = Ne[1] = 0;
int l = p.size();
for(int i = 1;i<l;i++){
int j = Ne[i];
while(j && p[i] != p[j]){
j = Ne[j];
}
if(p[i] == p[j]){
Ne[i+1] = j+1;
}
else{
Ne[i+1] = 0;
}
}
}
bool kmp(string s,string p){
int sl = s.size();
int pl = p.size();
int j = 0;
for(int i = 0;i<sl;i++){
while(j && s[i] != p[j]) j = Ne[j];
if(s[i] == p[j]) j++;
if(j == pl){ return 1;}
}
return 0;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin>>TT;
while(TT--){
cin>>n;
for(int i = 1;i<=n;i++) ans[i] = 0;
memset(t[0].son,0,sizeof(t[0].son));
t[0].fail = 0;
t[0].end = 0;
cin>>T>>C;
getnext(C);
for(int i = 1;i<=n;i++) cin>>s,insert(s,i),cin>>Q[i];
getfail();
query(T);
topo();
Ans.clear();
for(int i = 1;i<=cnt;i++) in[i] = 0;
for(int i = 1;i<=n;i++){
if(ans[pos[i]]){
if(Q[i].size()<C.size()) continue;
if(kmp(Q[i],C)) Ans.push_back(i);
}
}
if(Ans.size() == 0) cout<<'\n';
for(int i = 0;i<(int)Ans.size();i++){
cout<<Ans[i];
if(i != (int)Ans.size()-1) cout<<" ";
else cout<<'\n';
}
}
return 0;
}
A，即 HDU7445，鸡爪。本题由“鱼”负责，在“张”对 K 进行实现时在某知名图论编辑器网站上进行乱搞，并迅速发现了一个简单的构造方法，并且可以达到理论鸡爪构造量上界。于是，本题在未经证明的情况下提交并 AC，且成为了本次校内唯一一个没有在本题吃罚时的队伍。
在 \(n\le 5\) 时特判，其余在 \(1,2,3\) 节点上各增加一条边即可。
#include<iostream>
using namespace std;
const int N=1e5+10;
int n,u1,u2,u3;
void run(){
scanf("%d",&n);
u2=n/3+2;
u3=u2-1;
u1=u2+1+n%3;
if(n<=5)
{
for(int i=1;i<=n;i++)
{
printf("%d %d\n",1,i+1);
}
return;
}
for(int i=2;i<=u1;i++)printf("%d %d\n",1,i);
for(int i=3;i<=u2;i++)printf("%d %d\n",2,i);
for(int i=4;i<=u3;i++)printf("%d %d\n",3,i);
}
int main(){
int T=1;
scanf("%d",&T);
while(T--)run();
}
C，即 HDU7447，绝对不模拟的简单魔方。本题由“张”负责，选择了码量最大的模拟写法，并在第一次提交时成功 AC。
#include<bits/stdc++.h>
using namespace std;
int p[2500][4],tot,n,m,t,b[4],cntl,cntr,cnt;
char c[20][20],d[20][20],f[20],a[5][5];
bool vis1,vis2;
int ans1,ans2,ans3;
void dfs(int x){
if(x>3){
tot++;
for(int i = 1;i<=3;i++) p[tot][i] = b[i];
return;
}
for(int i = 0;i<=12;i++){
b[x] = i;
dfs(x+1);
}
}
void xz(int x,int y,int op){
for(int i = x;i<=x+1;i++)
for(int j = y;j<=y+1;j++)
a[i][j] = d[i][j];
if(op == 1){
d[x][y] = a[x][y+1];
d[x][y+1] = a[x+1][y+1];
d[x+1][y] = a[x][y];
d[x+1][y+1] = a[x+1][y];
}
else{
d[x][y] = a[x+1][y];
d[x][y+1] = a[x][y];
d[x+1][y] = a[x+1][y+1];
d[x+1][y+1] = a[x][y+1];;
}
}
void check(){
// for(int i = 1;i<=n;i++){
// for(int j = 1;j<=m;j++){
// cout<<d[i][j];
// }
// cout<<endl;
// }
int pos = 0,p1,p2,p3;
if(d[2][3] != '1' || d[3][2] != '2' || d[3][3] != '3') pos++,p1 = 1,p2 = 2,p3 = 3;
if(d[2][4] != '1' || d[3][4] != '3' || d[3][5] != '4') pos++,p1 = 1,p2 = 3,p3 = 4;
if(d[4][2] != '2' || d[5][3] != '6' || d[4][3] != '3') pos++,p1 = 2,p2 = 3,p3 = 6;
if(d[4][4] != '3' || d[4][5] != '4' || d[5][4] != '6') pos++,p1 = 3,p2 = 4,p3 = 6;
if(d[1][3] != '1' || d[3][1] != '2' || d[3][8] != '5') pos++,p1 = 1,p2 = 2,p3 = 5;
if(d[6][3] != '6' || d[4][1] != '2' || d[3][8] != '5') pos++,p1 = 2,p2 = 5,p3 = 6;
if(d[1][4] != '1' || d[3][6] != '4' || d[3][7] != '5') pos++,p1 = 1,p2 = 4,p3 = 5;
if(d[6][4] != '6' || d[4][6] != '4' || d[4][7] != '5') pos++,p1 = 4,p2 = 5,p3 = 6;
if(pos == 0) vis1 = 1;
if(pos == 1){
vis2 = 1;
ans1 = p1,ans2 = p2,ans3 = p3;
}
}
void work(){
for(int i = 1;i<=3;i++){
if(p[tot][i] == 0) continue;
if(p[tot][i] == 1){
f[1] = d[3][7];
f[2] = d[3][8];
for(int i = 8;i>=3;i--) d[3][i] = d[3][i-2];
d[3][1] = f[1];
d[3][2] = f[2];
xz(1,3,1);
}
if(p[tot][i] == 2){
f[1] = d[4][7];
f[2] = d[4][8];
for(int i = 8;i>=3;i--) d[4][i] = d[4][i-2];
d[4][1] = f[1];
d[4][2] = f[2];
xz(5,3,0);
}
if(p[tot][i] == 3){
f[1] = d[5][3];
f[2] = d[6][3];
for(int i = 6;i>=3;i--) d[i][3] = d[i-2][3];
d[1][3] = d[4][8];
d[2][3] = d[3][8];
d[3][8] = f[2];
d[4][8] = f[1];
xz(3,1,0);
}
if(p[tot][i] == 4){
f[1] = d[5][4];
f[2] = d[6][4];
for(int i = 6;i>=3;i--) d[i][4] = d[i-2][4];
d[1][4] = d[4][7];
d[2][4] = d[3][7];
d[3][7] = f[2];
d[4][7] = f[1];
xz(3,5,1);
}
if(p[tot][i] == 5){
f[1] = d[3][2];
f[2] = d[4][2];
f[3] = d[5][3];
f[4] = d[5][4];
f[5] = d[3][5];
f[6] = d[4][5];
f[7] = d[2][3];
f[8] = d[2][4];
d[5][3] = f[1];
d[5][4] = f[2];
d[4][5] = f[3];
d[3][5] = f[4];
d[2][3] = f[5];
d[2][4] = f[6];
d[4][2] = f[7];
d[3][2] = f[8];
xz(3,3,1);
}
if(p[tot][i] == 6){
f[1] = d[3][1];
f[2] = d[4][1];
f[3] = d[6][3];
f[4] = d[6][4];
f[5] = d[3][6];
f[6] = d[4][6];
f[7] = d[1][3];
f[8] = d[1][4];
d[6][3] = f[1];
d[6][4] = f[2];
d[4][6] = f[3];
d[3][6] = f[4];
d[1][3] = f[5];
d[1][4] = f[6];
d[4][1] = f[7];
d[3][1] = f[8];
xz(3,7,0);
}
if(p[tot][i] == 7){
for(int j = 1;j<=3;j++){
f[1] = d[3][7];
f[2] = d[3][8];
for(int i = 8;i>=3;i--) d[3][i] = d[3][i-2];
d[3][1] = f[1];
d[3][2] = f[2];
xz(1,3,1);
}
}
if(p[tot][i] == 8){
for(int j = 1;j<=3;j++){
f[1] = d[4][7];
f[2] = d[4][8];
for(int i = 8;i>=3;i--) d[4][i] = d[4][i-2];
d[4][1] = f[1];
d[4][2] = f[2];
xz(5,3,0);
}
}
if(p[tot][i] == 9){
for(int j = 1;j<=3;j++){
f[1] = d[5][3];
f[2] = d[6][3];
for(int i = 6;i>=3;i--) d[i][3] = d[i-2][3];
d[1][3] = d[4][8];
d[2][3] = d[3][8];
d[3][8] = f[2];
d[4][8] = f[1];
xz(3,1,0);
}
}
if(p[tot][i] == 10){
for(int j = 1;j<=3;j++){
f[1] = d[5][4];
f[2] = d[6][4];
for(int i = 6;i>=3;i--) d[i][4] = d[i-2][4];
d[1][4] = d[4][7];
d[2][4] = d[3][7];
d[3][7] = f[2];
d[4][7] = f[1];
xz(3,5,1);
}
}
if(p[tot][i] == 11){
for(int j = 1;j<=3;j++){
f[1] = d[3][2];
f[2] = d[4][2];
f[3] = d[5][3];
f[4] = d[5][4];
f[5] = d[3][5];
f[6] = d[4][5];
f[7] = d[2][3];
f[8] = d[2][4];
d[5][3] = f[1];
d[5][4] = f[2];
d[4][5] = f[3];
d[3][5] = f[4];
d[2][3] = f[5];
d[2][4] = f[6];
d[4][2] = f[7];
d[3][2] = f[8];
xz(3,3,1);
}
}
if(p[tot][i] == 12){
for(int j = 1;j<=3;j++){
f[1] = d[3][1];
f[2] = d[4][1];
f[3] = d[6][3];
f[4] = d[6][4];
f[5] = d[3][6];
f[6] = d[4][6];
f[7] = d[1][3];
f[8] = d[1][4];
d[6][3] = f[1];
d[6][4] = f[2];
d[4][6] = f[3];
d[3][6] = f[4];
d[1][3] = f[5];
d[1][4] = f[6];
d[4][1] = f[7];
d[3][1] = f[8];
xz(3,7,0);
}
}
}
check();
}
int main(){
dfs(1);
cin>>t;
cnt = tot;
while(t--){
cntl = 0;
n = 9,m = 12;
tot = cnt;
for(int i = 1;i<=n;i++)
for(int j = 1;j<=m;j++)
cin>>d[i][j];
for(int i = 1;i<=n;i++){
if(i == 2 || i == 5 || i == 8) continue;
cntl++;
cntr = 0;
for(int j = 1;j<=m;j++){
if(j == 2 || j == 5 || j == 8 || j == 11) continue;
cntr++;
c[cntl][cntr] = d[i][j];
}
}
n = 6,m = 8;
/*for(int i = 1;i<=n;i++){
for(int j = 1;j<=m;j++)
cout<<c[i][j];
cout<<endl;
}*/
vis1 = vis2 = 0;
while(tot){
for(int i = 1;i<=n;i++)
for(int j =1 ;j<=m;j++)
d[i][j] = c[i][j];
//for(int i = 1;i<=3;i++) cout<<p[tot][i]<<" ";
//cout<<endl;
work();
tot--;
if(vis1){
cout<<"No problem"<<'\n';
break;
}
if(vis2){
cout<<ans1<<" "<<ans2<<" "<<ans3<<'\n';
break;
}
}
/*for(int i = 1;i<=n;i++)
for(int j =1 ;j<=m;j++)
d[i][j] = c[i][j];
//xz(3,3,0);
work();
for(int i = 1;i<=n;i++){
for(int j = 1;j<=m;j++)
cout<<d[i][j];
cout<<endl;
}*/
}
return 0;
}
H，即 HDU7452，成长，生命，幸福。本题为规律题，由“马”负责，因为初始化问题十分不幸地吃了 \(7\) 发罚时，并有惊无险地在比赛接近结束时获得了 AC。
#include<iostream>
#include<vector>
using namespace std;
const int N=1e5+10,mod=1e9+7;
int n,m,deg[N],mx1[N];
using ll=long long;
ll dp[N];
int c2[N],c3[N],s3[N],pw;
vector<int> road[N];
int rt;
void dfs(int u,int f)
{
if(m<28) dp[u]=1ll*c2[u]*pw+1ll*s3[u]*(pw-1)+c3[u];
else dp[u]=c2[u]+s3[u];
if(dp[u]>dp[rt]) rt=u;
for(int i=0;i<road[u].size();i++){
int v=road[u][i];
if(v==f) continue;
c2[v]=c2[u]+(deg[v]==2);
c3[v]=c3[u]+(deg[v]>=3);
s3[v]=s3[u]+(deg[v]>=3?deg[v]-1:0);
dfs(v,u);
}
}
int qpow(int a,int b){
int ans=1;
while(b){
if(b&1) ans=1ll*ans*a%mod;
a=1ll*a*a%mod;
b=b>>1;
}
return ans;
}
// 直径=直径度数和
void run(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
deg[i]=0;
road[i].clear();
}
if(n==1)
{
puts("1");
return;
}
for(int i=1,x,y;i<n;i++)
{
scanf("%d%d",&x,&y);
road[x].emplace_back(y);
road[y].emplace_back(x);
deg[x]++;
deg[y]++;
}rt=0;
pw=qpow(2,m);
c2[1]=(deg[1]==2);
c3[1]=(deg[1]>=3);
s3[1]=(deg[1]>=3?deg[1]-1:0);
dfs(1,0);
c2[rt]=(deg[rt]==2);
c3[rt]=(deg[rt]>=3);
s3[rt]=(deg[rt]>=3?deg[rt]-1:0);
dfs(rt,0);
//printf("%d\n",ans);
int res=(1ll*pw*c2[rt]%mod+1ll*(pw+mod-1)*s3[rt]%mod)%mod;
int ans=(1ll*res%mod+c3[rt]+2)%mod;
printf("%d\n",ans);
}
int main(){
int T=1;
scanf("%d",&T);
while(T--)run();
}
总结：打 CF 逝有用的。
2024/8/12 - NOIP 比赛 \(5\)
第三次自闭。
详情：
又是熟悉的总结环节。
分数：\(0+0+60+0=60\)。现实意义上垫底。
T1，写 \(m'=s'=2n\) 的情况，本来得 \(40\) 分，结果文件名写错了爆零。（conveyer \(\rightarrow\) conveyor）
T2，暴力写挂了。这题才是没有大样例。
T3，通过打表找到 \(O(\max_{i=1}^n \text{dep}_i\times m)\) 的写法，得到 \(n^2\) 以及随机树结构的分数，\(60\) 分。
T4，写不了一点。
cyb 学长真的对 NOIP 难度没有一丁点的误解吗？
2024/8/13 - NOIP 比赛 \(6\)
第四次自闭，不过情况比上次好一点。
分数：\(100+0+20+0=120\)。排名 \(10/24\)。
一位喜欢计数的大佬出的，然后全是计数题。
T1，通过瞪样例瞪出了答案计算公式，然后用树状数组过了。
T2，看一眼后直接放弃，因为完全没有任何思路。
T3，全场将近 \(\frac{3}{4}\) 的时间都用在了这道题上，结果一个公式推错了，在整个调试过程中都没有察觉，最后只得打最低档暴力得 \(20\) 分。
T4，直接放弃。
总结：世界上不会有任何一场选拔性 OI 比赛只考计数。
2024/8/19 - NOIP 比赛 \(10\)
读者们可能注意到了，这次更新与上次更新已经相隔了一周之久。你们肯定很好奇为什么。
现在我可以说出答案了。
我玉玉了。
在过去的一周里，我所参加的所有比赛中，我都得到了极低的名次。这使我感到非常无法接受。今天的比赛中，我又排到了中位数的位置。这时我才想起来，我已经连续两年在校内比赛中稳定地排在中间的位置了。
我需要接受这个事实。
离正式比赛只剩两周了。
我需要重新调整自己的心态。
今天的比赛，考点为单调栈/最短路径树/状态压缩DP/模拟。
分数：\(100+20+0+10=130\)。
T1，一道单调栈优化题目。我已经很久没有在赛时使用过单调栈了。今天重新开始使用，取得了不错的效果。
T2，一道神秘最短直径题目，然而我没有看出 bitset 的成分，于是贪心选取度数最大的节点进行构造，然后理所当然地寄掉了。
T3，当时看到 \(1\le n\le 15\)，直接怕了，没有打。
T4，手搓了一个非常长的表达式，然后寄了。
总结：要敢打。
2024/8/20 - NOIP 比赛 \(11\)
我们为何而存在？
你说得对，但是我已经死了。
分数：\(41+30+20+0=91\)。
T1，思路完全错误。我的思路是，用尽可能少的线程录下所有视频，并选取包含视频最多的 \(k\) 个线程，累加答案。得分 \(42\) 分。为什么最终是 \(41\) 分？因为我在最后用更大的时间复杂度再次实现了这个错误的思路。
T2，比赛开始就完全放弃了这道题，在将近结束时打暴力，得到最低档部分分。
T3，尝试推一些神秘图论与数论结合的方法，结果完全没有成果，只好打最低档暴力。
T4，本来同样能有最低档暴力分 \(30\) 分，但是因为与 mmx 同样卡进了神秘过编不运行的内存区间，导致 0ms 128KiB RE。
总结：我已经死了。
2024/8/21 - ICPC 比赛 \(6\)
我复活了。
本次比赛的来源为杭电“钉耙编程”中国大学生编程超级竞赛 \(4\)。
这场比赛，某种程度上可以被称作乱搞场。
T5，多层血条。
签到题 \(1\)。
直接按照题意模拟即可。
- 负责人：Redshift_Shine。
- 罚时数量：\(2\)。
- 死因：使用蒙版策略实现，结果在做除法时会使颜色偏移一位。
#include <cstdio>
using namespace std;
const int N = 5e1 + 10, M = 8e2 + 10;
char ch[N][M], tch;
int n, m, hp, dmg, tre;
void run()
{
scanf("%d%d%d%d", &n, &m, &hp, &dmg);
if (hp < m)
tch = ' ';
else
tch = 'A' + ((hp / m + 4) % 5);
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
ch[i][j] = tch;
}
if (hp % m)
{
tre = (hp - 1) % m + 1;
if (tch == ' ')
tch = 'A';
else
tch = (tch == 'E' ? 'A' : tch + 1);
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= tre; j++)
ch[i][j] = tch;
}
}
else
tre = m;
tch = '.';
for (int i = 0, t = tre; i < dmg and i < m; i++, t = (t == 1 ? m : t - 1))
{
for (int j = 1; j <= n; j++)
{
ch[j][t] = tch;
}
}
putchar('+');
for (int i = 1; i <= m; i++)
{
putchar('-');
}
puts("+");
for (int i = 1; i <= n; i++)
{
putchar('|');
for (int j = 1; j <= m; j++)
{
putchar(ch[i][j]);
}
puts("|");
}
putchar('+');
for (int i = 1; i <= m; i++)
{
putchar('-');
}
puts("+");
}
int main()
{
int T = 1;
scanf("%d", &T);
while (T--)
run();
}
T9，昵称检索。
签到题 \(2\)。
使用 vector 容器计算每个名称最先出现的位置，使用同样的方法计算一年 \(\bold{366}\) 天的最晚出现位置（本题一律按闰年计算）。做后缀和即可。
- 负责人：Redshift_Shine。
- 罚时数量：\(1\)。
- 死因：空间开小。
#include <algorithm>
#include <iostream>
#include <string>
#include <vector>
using namespace std;
const int M = 1e6 + 10, N = 1e5 + 10, T = 1e3 + 10;
string s[M], t, dat[M];
int n, m, ps[M], pre[M], pos[M], idx, res = 0;
const int dx[]{31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
using pii = pair<int, int>;
vector<pii> ch[26], tmp;
void run()
{
res = 0;
scanf("%d%d", &n, &m);
cin >> t;
for (int i = 0; i < 26; i++)
ch[i].clear();
for (int i = 1; i <= n; i++)
{
pos[i] = m;
cin >> s[i];
ch[s[i][0] - 'a'].emplace_back(i, 0);
}
for (int i = 0; i < m; i++)
{
ps[i] = 0;
if (!isalpha(t[i]))
continue;
tmp = ch[t[i] - 'a'];
ch[t[i] - 'a'].clear();
for (auto &[k, v] : tmp)
{
v++;
if (v == s[k].size())
pos[k] = i;
else
ch[s[k][v] - 'a'].emplace_back(k, v);
}
}
for (int i = 0; i < 10; i++)
ch[i].clear();
for (int i = 1; i <= idx; i++)
{
ch[dat[i][0] - '0'].emplace_back(i, 0);
}
ps[m] = 0;
for (int i = m - 1; ~i; i--)
{
ps[i] += ps[i + 1];
if (!isdigit(t[i]))
continue;
tmp = ch[t[i] - '0'];
ch[t[i] - '0'].clear();
for (auto &[k, v] : tmp)
{
v++;
if (v == dat[k].size())
ps[i]++;
else
ch[dat[k][v] - '0'].emplace_back(k, v);
}
}
for (int i = 1; i <= n; i++)
{
res += ps[pos[i]];
}
printf("%d\n", res);
}
string to_str(int x)
{
if (x < 10)
{
string tmp2 = "";
tmp2 += (x + '0');
return tmp2;
}
return to_str(x / 10) + (char)(x % 10 + '0');
}
int main()
{
for (int i = 0; i < 12; i++)
{
for (int j = 1; j <= dx[i]; j++)
{
idx++;
dat[idx] = to_str(i + 1);
if (i < 9)
dat[idx] = '0' + dat[idx];
if (j < 10)
dat[idx] += '0';
dat[idx] += to_str(j);
if (dat[idx].size() != 4)
dat[idx] = '0' + dat[idx];
reverse(dat[idx].begin(), dat[idx].end());
}
}
int T = 1;
scanf("%d", &T);
while (T--)
run();
}
T3，最优 K 子段。
二分答案。
每次遍历整个数组，发现后缀满足条件的子段出现，直接清空备选位置。
时间复杂度 \(O(n\log n\log V)\)。
- 负责人：Linyize257。
- 罚时数量：\(0\)。
#include <cmath>
#include <iostream>
#include <set>
#define int long long
using namespace std;
int t;
int n, m;
struct node
{
int x, y;
bool operator<(const node &u) const
{
return x < u.x;
}
};
bool vis[200005];
void init()
{
int num = 200000;
vis[0] = vis[1] = 1;
for (int i = 2; i <= num; i++)
{
if (vis[i])
continue;
for (int j = 2 * i; j <= num; j += i)
{
vis[j] = 1;
}
}
return;
}
int a[200005];
set<node> st;
int check(long long xx)
{
st.clear();
st.insert((node){0, 0});
int ans = 0;
for (int i = 1; i <= n; i++)
{
set<node>::iterator it = st.begin();
while (it != st.end())
{
if (a[i] - (it->x) < xx)
{
it = st.end();
continue;
}
if (!vis[i - (it->y)])
break;
it++;
}
if (it == st.end())
st.insert((node){a[i], i});
else
{
st.clear();
ans++;
st.insert((node){a[i], i});
}
}
return ans;
}
signed main()
{
cin >> t;
init();
while (t--)
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> a[i], a[i] += a[i - 1];
if (m * 2 > n)
{
cout << "impossible\n";
continue;
}
long long l = -2000, r = 200000000ll;
int ans = 0;
while (r - l > 1)
{
int mid = (l + r) >> 1;
if (check(mid) >= m)
{
l = mid;
}
else
r = mid;
}
cout << l << "\n";
}
return 0;
}
T7，序列更新。
本题是本场比赛中最精彩的题目，也是本场比赛中最体现团队合作精神的题目。在本场比赛中，存在一个长达一个小时以上的区间，在此区间内，几乎所有的团队都在尝试找出这题的解法。
在 Linyize257 完成了 T3 后，看着排行榜，再看到题目中的 \(6\) 秒限时（在 HDUOJ 是 \(10\) 秒）以及“随机”字眼，我们认为可以找到一种神秘的方法解决这道题。
首先，HH_yst 想到了一个性质，即较小的 \(b_i\) 在若干次操作后几乎不可能再对原序列造成修改。于是他建议，在前 \(\sqrt n\) 次操作中检查整个序列，而在后面的操作中只检查前 \(\sqrt n\) 大的 \(b_i\) 对序列造成的更改。与此同时，Redshift_Shine 提出另一种思路，即利用数据点数量极小（\(T=2\)）的性质为每一个询问动态分配随机采样检查 \(b_i\) 的修改可行性的次数。随后，Redshift_Shine 实现了 HH_yst 的思路，随后发现即使在随机生成的数据下，所有小 \(b_i\) 都在严格 \(\sqrt n\) 次修改中完成修改的几率还是极小。随后，Redshift_Shine 认为自己的思路实现难度极高，于是放弃了这个思路。
为了解决实现难度较高的问题，Redshift_Shine 提出另一种思路，即沿用 HH_yst 发现的性质，在前 \(\sqrt n\) 次操作中仍然检查整个序列，但在后面的操作中将 \(b\) 序列降序排序，在每次操作中将检查 \(b_i\) 的个数按一定比例减少。于是，Redshift_Shine 完成实现，并通过了样例。与此同时，考虑到本题对参数的要求可能较为苛刻，HH_yst 完成了暴力对拍程序的实现。随后，Redshift_Shine 也完成了按照题目要求的数据生成器的实现。
接下来半个小时中，Redshift_Shine 将自己的程序与 HH_yst 的程序进行对拍，然而每次调参的结果都不尽如人意。此时，HH_yst 将 Redshift_Shine 程序中的比例参数调为 \(1\)，结果发现答案仍然错误。此时，Redshift_Shine 终于发现了其代码中的错误。他浪费了整整半个小时。
在接下来的对拍中，Redshift_Shine 持续调整参数，最终在比例参数调为 \(0.9975\) 且 \(n=2\times 10^4\) 的情况下与对拍程序的输出结果完全一致。
于是 Redshift_Shine 提交了代码。Wrong Answer。然后他对着代码端详良久，惊呼一声：“我参数呢？”原来，他提交了之前被证明为错误解法的代码。
接下来，Redshift_Shine 重新找到了他的代码然后再次提交。Wrong Answer。这是怎么回事？此时，HH_yst 提出了一种新的思路。他认为，既然 \(n=2\times 10^4\) 已经不足以找出代码的错误，那么不妨使用两份参数不同的代码对拍，并且将 \(n\) 调至最大值 \(2.5\times 10^5\)。
于是 Redshift_Shine 将代码复制一份，并将比例参数调至 \(0.9999\)，并且按照 HH_yst 的方法继续对拍。
效果是极为显著的。仅仅在第一组样例中，两组代码就给出了不同的答案。于是，我们按照这种方法继续对拍并调整参数，终于，在参数调为 \(0.99945\) 时，其输出与参数调为 \(0.9999\) 时保持一致，并且运行时间被控制在了 \(5\) 秒左右。此时，Redshift_Shine 准备提交，但 HH_yst 提议再进行一组测试，检测这个参数与 \(0.9975\) 是否存在区别。
本次对拍仍然是成功的。参数为 \(0.99945\) 的代码输出显著大于参数为 \(0.9975\) 的代码输出。
于是，我们在比赛进行至 \(3\) 小时 \(19\) 分 \(2\) 秒提交了参数为 \(0.99945\) 的代码，并取得 Accepted。
- 负责人：HH_yst / Redshift_Shine。
- 罚时数量：\(2\)。
- 死因：提交错误代码，对拍不完善。
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 2.5e5 + 10;
using pii = pair<int, int>;
int a[N], sqt, n, m, pt;
bool vis[N];
using ll = long long;
using pii = pair<int, int>;
pii b[N];
ll res;
using ld = long double;
const ld eps = 0.99945;
ld prp;
int tmp;
void run()
{
res = 0;
scanf("%d%d", &n, &m);
prp = n;
sqt = sqrt(n);
memset(vis, 0, n);
for (int i = 0; i < n; i++)
{
scanf("%d", a + i);
res += a[i];
}
for (int i = 0; i < n; i++)
{
scanf("%d", &b[i].first);
b[i].second = i;
}
sort(b, b + n);
for (int i = 1, x, tm = 0; i <= m; i++)
{
scanf("%d", &x);
if (vis[x])
continue;
if (n <= 10000 or tm <= sqt)
{
for (int j = 0; j < n; j++)
{
pt = (b[j].second + n - x) % n;
if (a[pt] < b[j].first)
{
res -= a[pt];
a[pt] = b[j].first;
res += a[pt];
}
}
tm++;
}
else
{
tmp = prp;
tmp = max(tmp, sqt);
for (int j = 0; j < tmp; j++)
{
pt = (b[n - j].second + n - x) % n;
if (a[pt] < b[n - j].first)
{
res -= a[pt];
a[pt] = b[n - j].first;
res += a[pt];
}
}
prp *= eps;
}
printf("%lld\n", res);
}
}
int main()
{
int T = 1;
scanf("%d", &T);
while (T--)
run();
}
2024/8/22 - NOIP 比赛 \(12\)
我又死了一遍。
我无法确定我是不是处于死与活的中间态内。
分数：\(100+75+30+32=239\)。
T1，看到题目直接想到平均分配，然后很快地打了出来。第一次打完后发现空间开小了，然后开大后就过了。
T2，打完 T1 之后将近 \(10\) 分钟处于思想混乱状态，然后看 T2，猛然想到可以二分答案。然后马上一顿打，大样例过了，交。万万没想到读题不仔细，漏掉了 NO 的情况，然后少了 \(25\) 分。
T3，完全没有头绪，直接打暴力。小样例过了，交。然后没测大样例。比赛结束前 \(10\) 分钟检查的时候发现没测大样例，然后赶紧下载下来测，发现 WA 了。猛然发现自己的交集判断有问题，然后改了。改完之后，答案对了，交。过于惊险。
T4，感觉和点分树或者虚树有点关系，然后想不出来了，就打了暴力和菊花图的特殊性质，加起来 \(32\) 分。
从第 \(10\) 掉到了第 \(14\)，大亏。要是有 \(4\) 次都在第 \(3\) 梯队的话就真的无地自容了。
2024/8/23 - NOIP 比赛 \(13\)
\(2024\) 年 \(8\) 月 \(23\) 日上午 \(11\) 时 \(45\) 分，正当所有人都在为 T3 的特殊性质和 T4 的策略做出最后的努力时，忽然，所有人的电脑变为了黑屏，屏幕下的电源指示灯熄灭。此时，一些将代码存在 C 盘的同学痛哭流涕，而其他将代码存在 D 盘的同学开心地向饭堂奔去。
“chxulong，我们有麻烦了。”
分数，\(100+100+40+5=245\)。排名未知。
T1，一个并不十分显然的 DP 优化。将题目给出的伤害表达式拆开可得
因此，在选择的怪物确定的情况下，有显然的贪心策略，即按照 \((a+b)\) 降序的顺序击杀。
时间复杂度 \(O(n^2+m\log n)\)。
T2，比 T1 简单，正难则反，考虑计算出每个点不被选中的概率累加即可，时间复杂度 \(O(n)\)。
T3，不会，用并查集暴力，时间复杂度 \(O(n^2)\)，\(40\) 分。
T4，推不出“最优策略”，骗树的分，\(5\) 分。
总结：本来看到题目觉得有机会重回一梯队，这下好了，留在二梯队了，惨。
2024/8/24 - ICPC 全队娱乐赛
在今天，\(2024\) 暑假的集训迎来了尾声。与之而来的是一场为全队不同水平的选手设计的一场 ICPC 娱乐赛。在本场比赛中，我经历了一个幅度巨大的情绪波动，具体见下。
1. Ascending
在比赛开始的一刹那，我开始寻找签到题的位置。根据经验，签到题不会被放在第一道题，于是我开始看后面的题目。
当看到倒数第二道题时，我眼前一亮：这也许就是签到题。题意如下：
给出字符串 \(s\)，每次修改 \(s\) 中的一个字符，在每次修改后求子串 \(\texttt{tyte}\) 的出现次数。\(1\le |s|,q\le 10^6\)。
于是我想到，利用子串很短的性质，可以直接使用 substr 函数进行检查。每次修改字符时，只需要检查包含该字符的四个起始位置即可。
于是，在比赛开始 \(4\) 分 \(46\) 秒时，我成功获得了这道题目的首 A。
此时，看到另一位选手 A 掉了另一道题，我看到这道题：
给定 \(n\) 个长度为 \(m\) 的数组 \(a_i\)，以及一个长度为 \(m\) 的数组 \(b\)，要求选出若干个 \(a_i\) 使得选出的 \(a_i\) 对应位置的总和与 \(b\) 对应位置的值相等，求满足条件的方案数。\(1\le m\le 100\)。
本来看到这题，我以为是 DP。但我又看到一个小得惊人的数据范围：
\(1\le n\le 20\)
于是，我恍然大悟，枚举所有选择 \(a_i\) 的组合，检查是否符合要求，时间复杂度 \(O(2^nm)\)。
然后，我提交了代码，Runtime Error。
我想道，（不可发送单个标点符号），于是我再次检查自己的代码。
然后我发现，我数组开小了。
随后，我改大了数组大小，然后再次提交。
于是，我在比赛开始后 \(10\) 分钟 \(27\) 秒时取得了本题的 Accepted。
接下来，我看到有人做第 \(1\) 题，于是我去看：
给出正整数 \(d\)，请构造任意一组满足以下条件的非负整数三元组 \((a,b,c)\)，或报告无解：
\[\begin{cases} x>y>z\\ x-z=d\\ x\mid y+z\\ y\mid x+z\\ z\mid x+y\\ \end{cases} \]
然后，我想，什么玩意？怎么构造？
然后我看到了样例：
3 -> Impossible
4 -> 6 4 2
于是我猜，答案应该是：
然后我猜对了，在比赛开始 \(13\) 分钟 \(9\) 秒后取得了本题的 Accepted。
接下来，我看见了整整一列的罚时。于是我看到这道题。题意是这样的：
给出 \(n\) 个整数，保证其中有一个数的出现次数大于 \(\lfloor\frac{n}{2}\rfloor\)。求这个数。\(1\le n\le 10^7\)，时间限制 \(3\) 秒。
我想，这题应该不难啊。直到我看到了内存限制：4MiB。
当时我想，（不可发送单个标点符号），而且不知道摩尔投票算法，于是我想到了一种猎奇的方法：既然这个数的出现次数大于 \(\lfloor\frac{n}{2}\rfloor\)，那么这些数所占据的二进制位出现次数也必然大于 \(\lfloor\frac{n}{2}\rfloor\)，其他的二进制位出现次数会严格小于 \(\lfloor\frac{n}{2}\rfloor\)，所以本方案可行。于是我开始实现本题，并在比赛开始后 \(18\) 分钟 \(55\) 秒后在内存限制内解决了这道题，获得了首 A。然而，就在我得到了 Accepted 的那一刻，教练认为 4MiB 的限制过于苛刻，于是将内存限制上调至 40MiB，重测了之前提交的代码，最终使我的首 A 拱手让人。我对这个调整极为不满，当场提出了抗议，但无济于事。这也在一定程度上影响了我接下来比赛的情绪。
就在此时，我仍然处于排行榜的第一名。
接下来，我看到有人 A 了一道叫“罗德岛战役”的题。我点进去看，发现一堆东西，以为是个大模拟。然后我再仔细看，发现是个连普及难度都没有的小学数学题，然后在比赛开始后 \(34\) 分钟 \(14\) 秒后取得了本题的 Accepted。
接下来，突然有一位学长拿着他的两题首 A 冲到了我的前面。我顿感大事不妙，急忙去看他过掉的题。
给出一个有 \(m\) 棵树的森林，求用 \(m-1\) 条边连接每一棵树后整棵树的最大/最小直径。
然后我想，非常简单，最大直径就是将每一棵树的直径提取出来首尾相接，而最小直径就是提取出每条直径上的终点，以最长直径的中点为根构造菊花图。
然后，Wrong Answer。怎么回事？哦，原来我一堆变量写错了还忘记处理 corner case 了。去处理一下，然后在比赛开始后 \(1\) 小时 \(14\) 分 \(12\) 秒取得了本题的 Accepted。
本来我认为，我有希望超越那位学长，重新夺回第一。却不知，这是我排名大幅下降的开始。
2. Falling
接着，我看到了一道题。
在一条无限长的数轴上，有 \(n\) 个点。第 \(i\) 个点会在第 \(t_i\) 秒出现于 \(x_i\) 位置，接下来以 \(1\) 单位/秒的速度向左或右移动至 \(y_i\) 位置，然后消失。求不同方向运动的点的相遇次数。
于是我想到，可以使用坐标系转换此问题转换为以下形式：
给定 \(n\) 条线段，第 \(i\) 条线段的端点分别为 \((t_i,x_i),(t_i+|x_i-y_i|,y_i)\)，求互相垂直的线段的交点数。
于是我想到，可以通过将坐标系逆时针旋转 \(45\degree\) 转换为离线查询可以解决的问题。
然后我开始实现。一开始写的是不带离散化的动态开点线段树，然后吃了三发 Runtime Error。接下来，我加入离散化，然后吃了两发 Memory Exceeded。最后，我改成树状数组，然后吃了一发 Wrong Answer。为什么？原来是因为排序方法错了。重新写 cmp 函数，过了。此时距离比赛开始已经 \(4\) 小时 \(52\) 分钟 \(27\) 秒了。此时我放弃了对其他题目的思考，收拾书包去了饭堂。
没错。结束了。
2024/8/28 - 数/英/物 复习
数学
二次根式
表现形式：\(\sqrt a(a\ge 0)\)
定义：\(\sqrt{\quad}\) 被称为二次根号
计算法则：
最简二次根式
表现形式：\(2\sqrt 2,\frac{\sqrt 3}{10},\frac{2\sqrt a}{a}\)
定义：被开方数不含分母且不含能开得尽方的二次根式
形式化定义 \(\sqrt a\) 为最简二次根式当且仅当：
代数式
表现形式：\(5,a,a+b,-ab,\frac{s}{t},-x^3,\sqrt 3,\sqrt a(a\ge 0)\)
定义：用基本运算符号把数或表示数的字母连接起来的式子
海伦-秦九韶公式
函数
表现形式：
- 解析式
- 图像
- 表格
一次函数
一般解析式：\(y=kx+b(k\neq 0)\)
正比例函数：\(y=kx(k\neq 0)\)
分段一次函数：
二次函数
一般解析式：\(y=ax^2+bx+c(a\neq 0)\)
判别式：\(\Delta=b^2-4ac\)
求根公式：\(x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)
勾股定理
表现形式：\(a^2+b^2=c^2\)
应用：
| 公式 | 图片 |
|---|---|
| \(a^2+b^2=c^2\Rightarrow \text{Rt}\triangle ABC\) |  |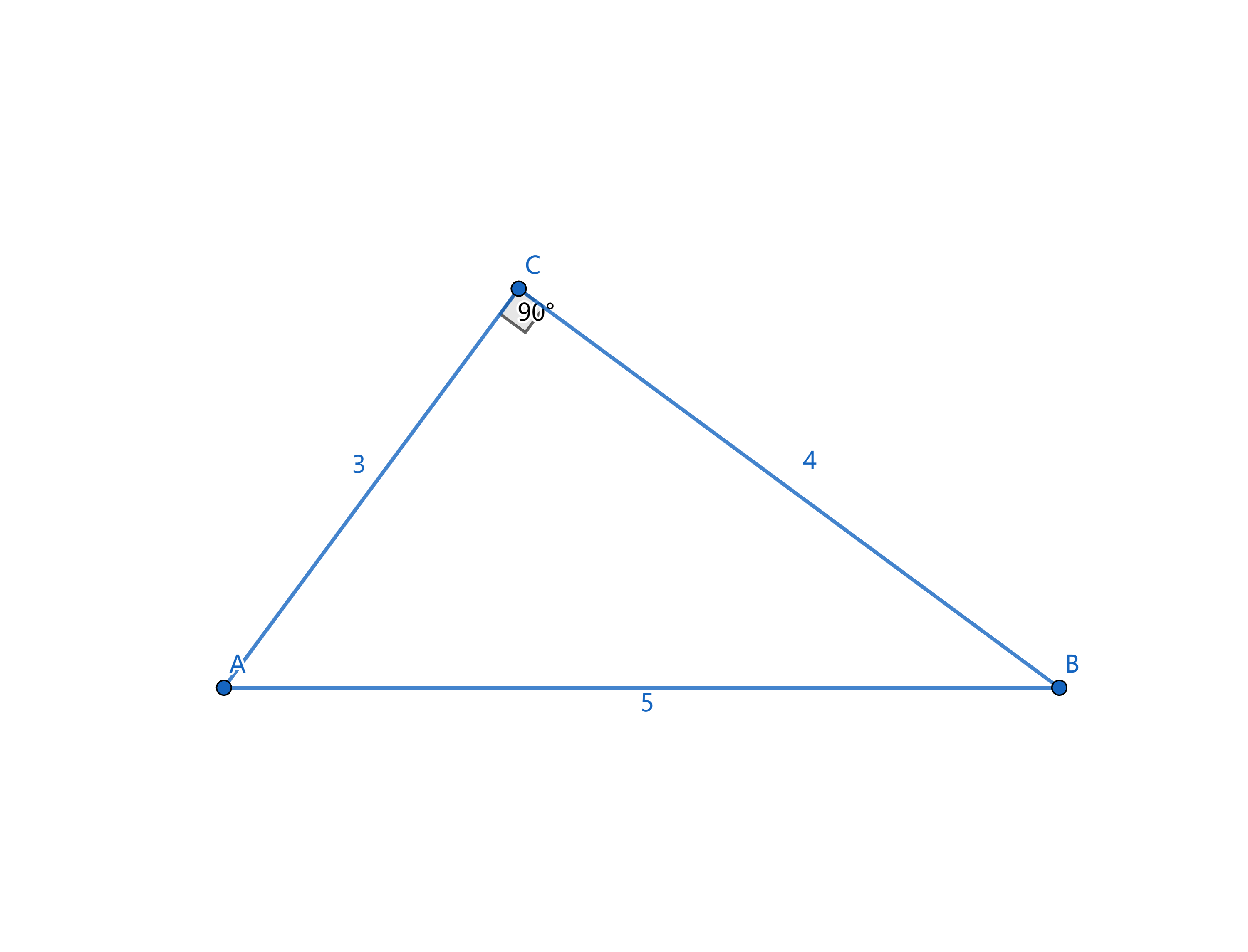
| \(a^2-d^2=b^2-(c-d)^2\) |  |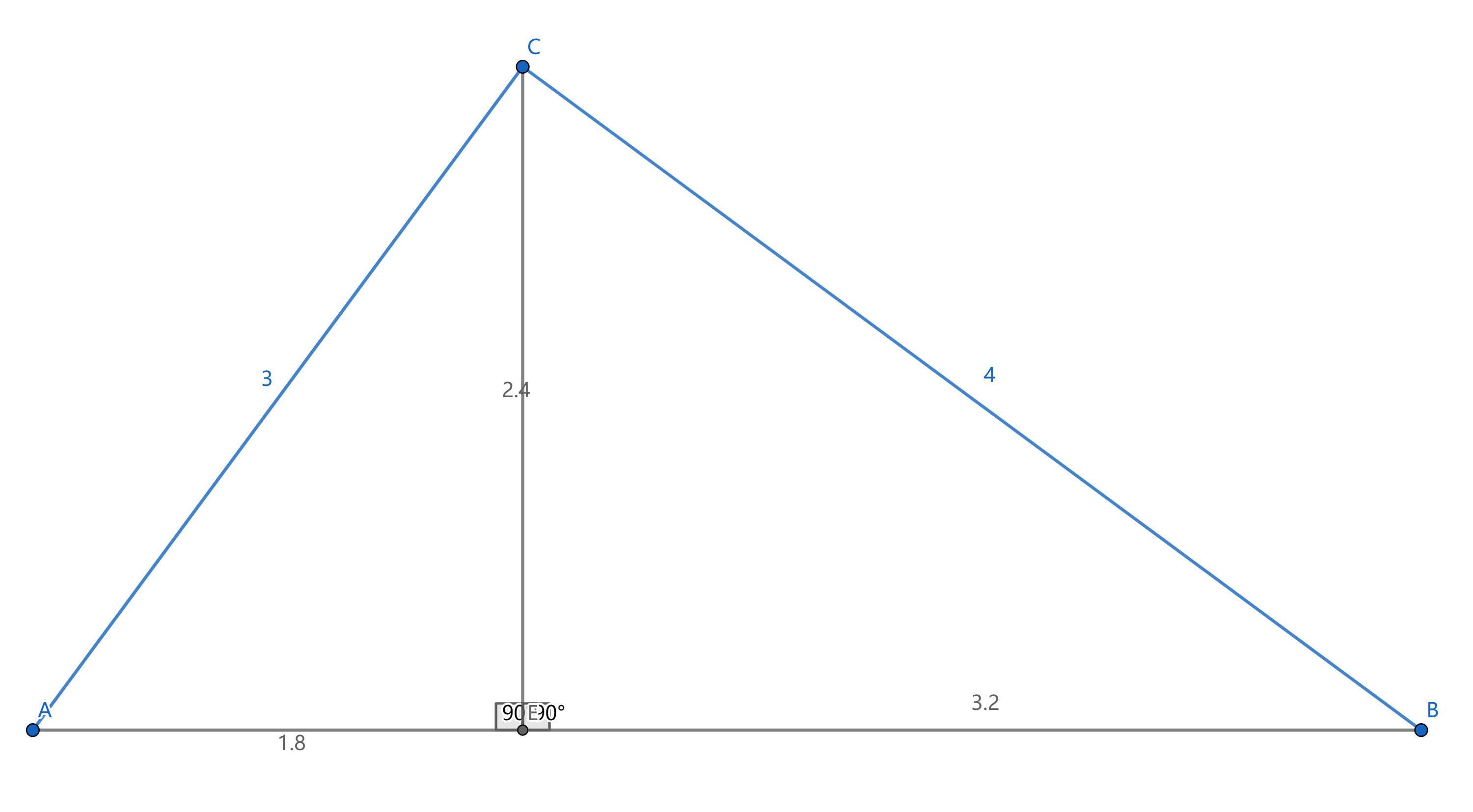
平行四边形
表现形式：\(\Box ABCD\)
定义：两组对边分别平行的四边形为平行四边形。
一般形态：
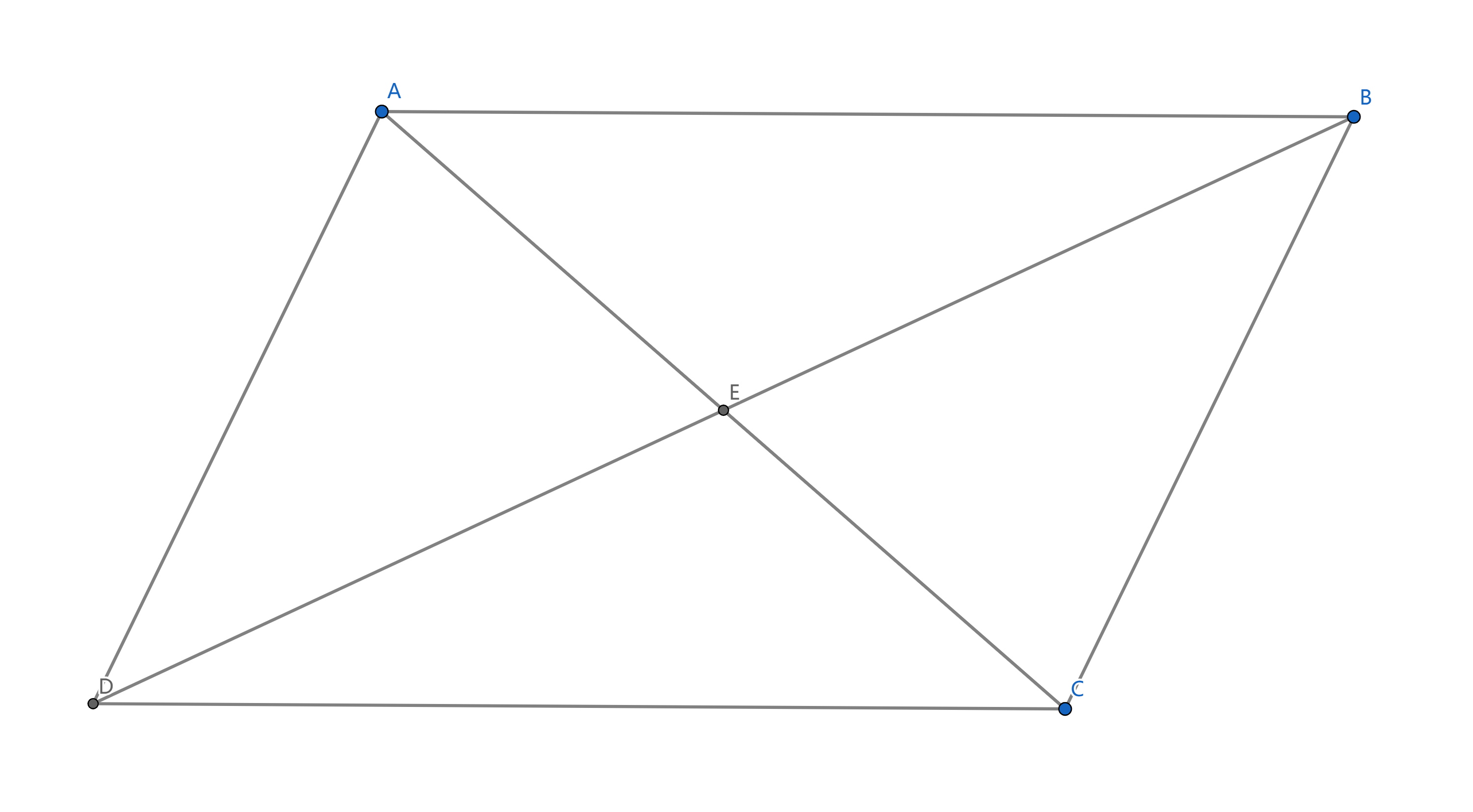
上方的平行四边形满足以下条件：
若将上方四边形看作一般四边形，那么当该四边形满足以下任一条件时，其为平行四边形：
中位线
在 \(\triangle ABC\) 中，若 \(E\) 为 \(AB\) 中点，\(F\) 为 \(AC\) 中点，则 \(EF\) 为 \(\triangle ABC\) 中位线且 \(EF=\frac{1}{2} BC\)，\(EF\parallel BC\)。
矩形
定义：有一个角是直角的平行四边形是矩形。
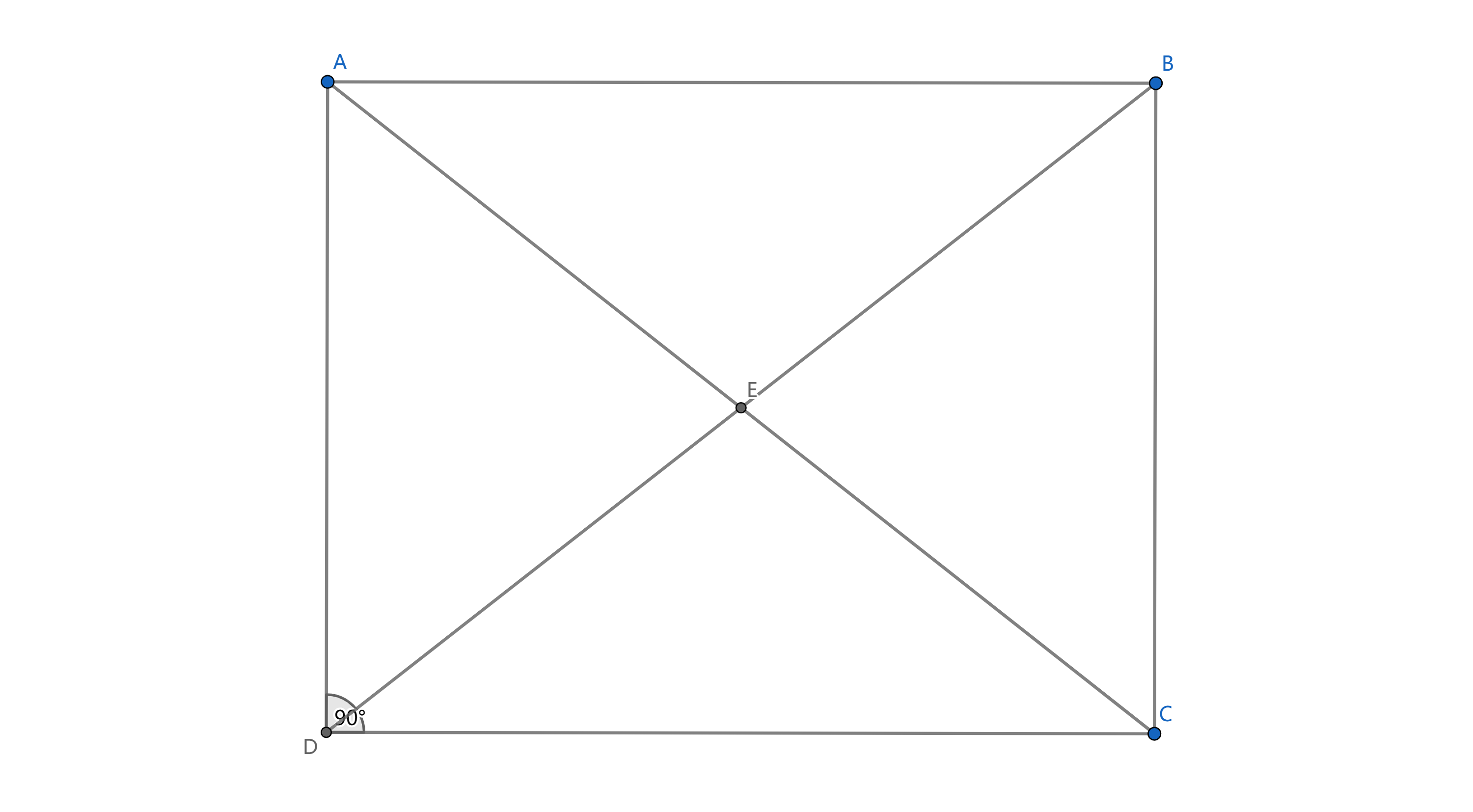
上述图形在满足平行四边形的全部性质前提下满足以下性质：
若将上方四边形看作一般平行四边形，则当该平行四边形满足以下任一条件时该图形为矩形：
若将上方四边形看作一般四边形，则当该四边形中出现三个直角时该四边形为矩形。
菱形
定义：有一组邻边相等的平行四边形是菱形。
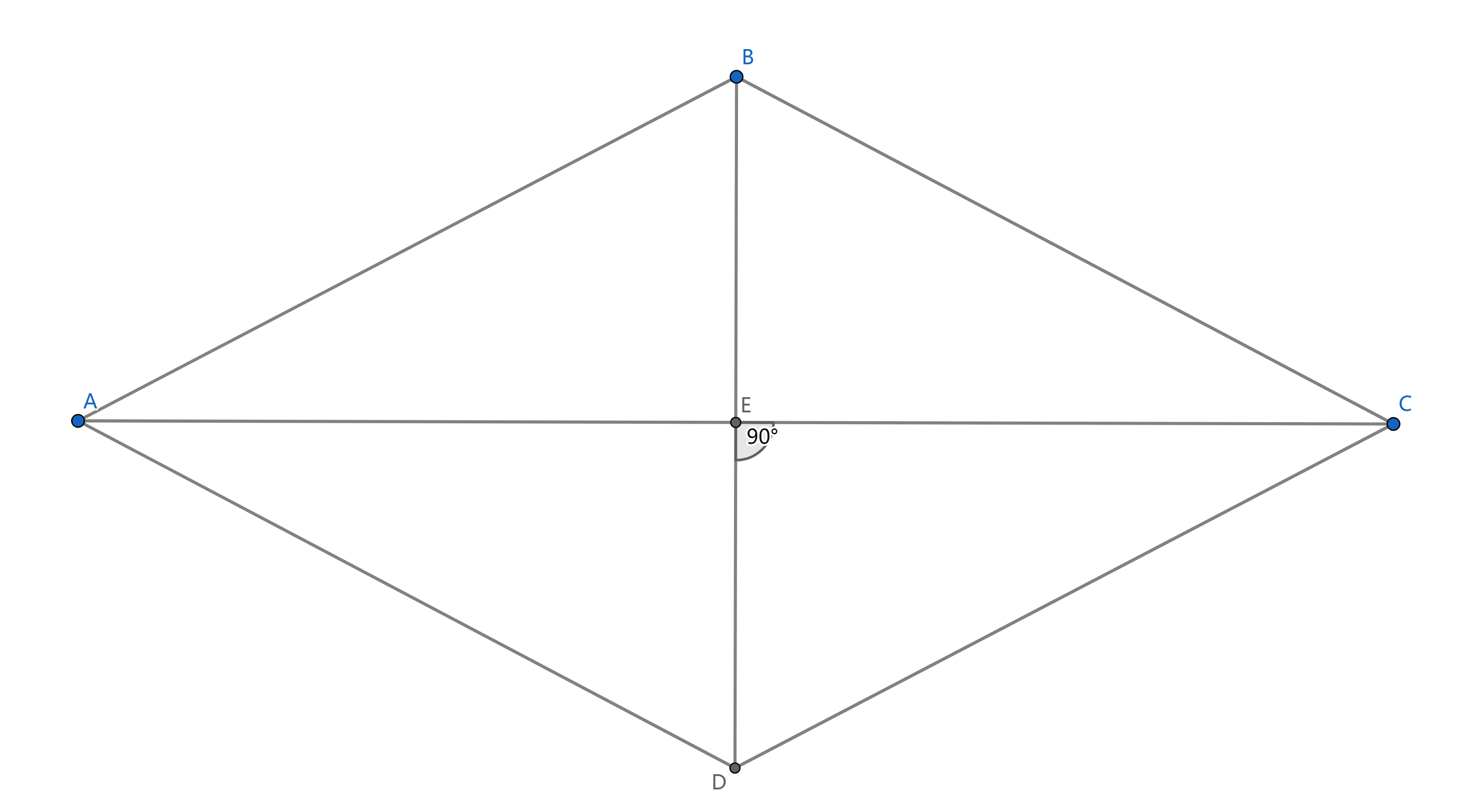
上述图形在满足平行四边形的全部性质前提下满足以下性质：
若将上方四边形看作一般平行四边形，则当该平行四边形满足以下任一条件时该图形为菱形：
若将上方四边形看作一般四边形，则当该四边形中满足以下任一条件时该图形为菱形：
正方形
定义：同时满足矩形与菱形性质的四边形为正方形。
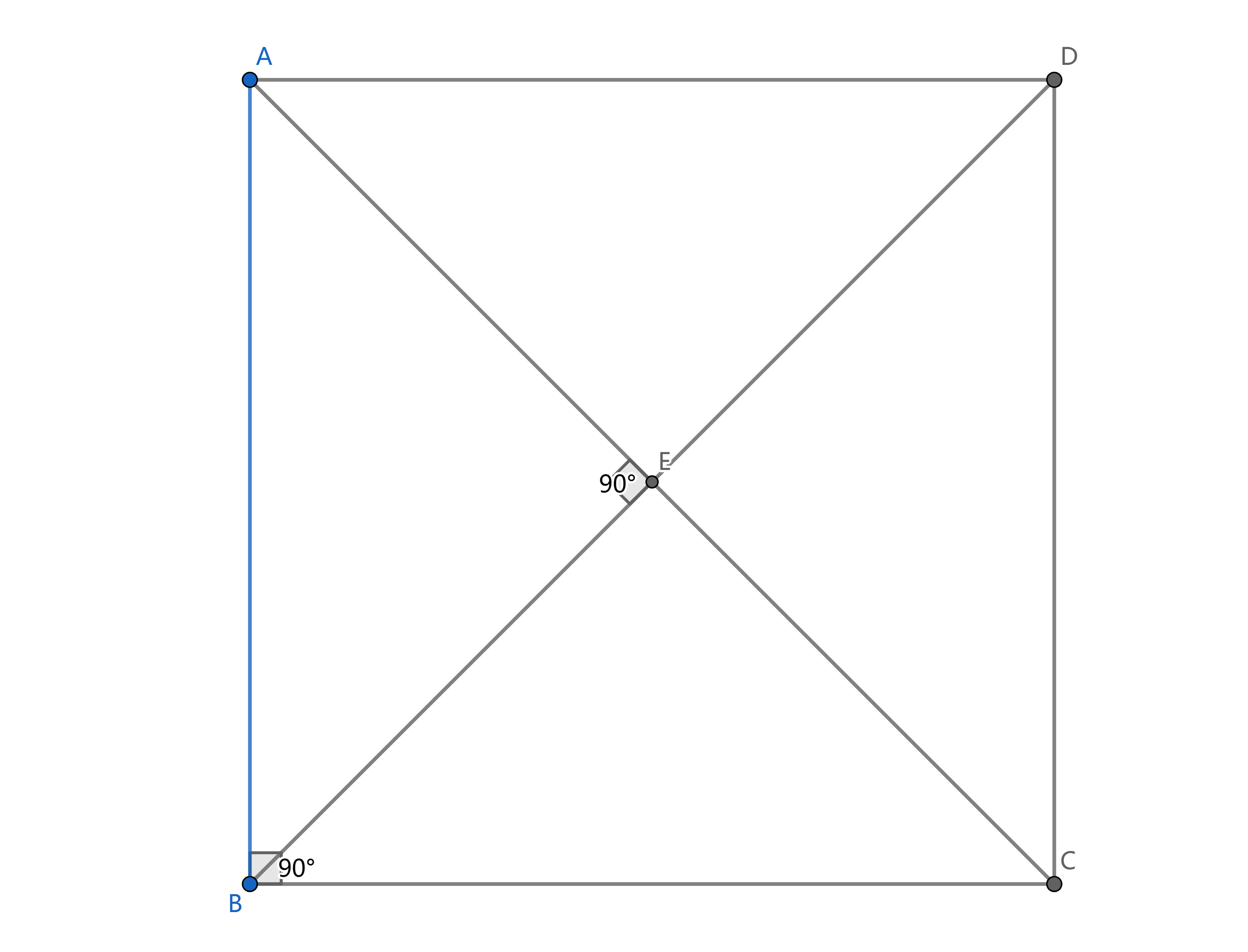
上述图形满足菱形与矩形的所有性质。
旋转
定义：平面图形绕平面内一点旋转一个特定角度，旋转前后图形的对应点被称为旋转对应点。
范例如下。
条件：\(\triangle ABC\cong\triangle AEF\)
格式：可将 \(\triangle ABC\) 旋转 \(\alpha\) 至 \(\triangle AEF\)，使 \(B\) 与 \(E\) 重合，\(C\) 与 \(F\) 重合。
英语
众所周知，英语无法复习。我妈说可以复习，所以复习一下。
Infinitive
verbs to infinitives (I consider it as do to do)
Example: I decide to meet that hacker.
Sometimes infinitive kills to.
Example: Mum made me go to bed early.
They can also be used as purpose expresser.
Example: I use computer to make programs.
Gerund
+ing. Yes, adding it to the back of the verb makes a gerund. (Way too easy)
Gerund as a subject matches with a singular-form verb.
Example: Programming is the main project of OI(Olympiad in Informatics).
It can be also used as a noun.
Example: Programming is my favourite.
Passive Voice
Passive sentences are different to the active sentences, because they just tell the truth. For example:
No nets are required for this type of fishing.
Passive Voice + Modal Verbs
Example:
It is [adj.] for [n./pn.] to [v.]
Tells us (dis)advantages of something.
Example: It's important for us to protect giant pandas.
[not] [adj.] enough to [v.]
Telling the completeness.
Example: They are strong enough to protect themselves.
Adverbs with Verbs
Telling happens or done.
Example: I'll do that carefully.
Adverbial Clause
[Because], [statement], [So].
Example: Because no one else saw these aliens, I refuse to believe you.
because of
[v.] because of [n.].
Example: Tina woke up at midnight because of a loud noise.
Past Continuous Tense
Happening in the past.
[n.] was/were doing.
Example: I was attending a contest last night.
物理
好像也就能记一下公式了。
2024/9/4 - 跨越
为期三天的开学考+风纪教育结束了。文科还是一如既往地差，理科还是一如既往地稳定。
从今天开始，我就是初三的学生了。在上一次更新和这次更新之间，我第一次在分离式 Div.2 比赛中 A 掉 \(5\) 题，成为了 Candidate Master；同时也第一次 AK 了 AtCoder Beginner Contest。我不知道这暗示了什么，但可以肯定的是，我离完全回归文化课不远了。等到那一天，我的更新频率必定迎来腰斩。
总之，我也只能向前看了啊。
2024/9/7 - 两周
开学考的成绩虽然没有出来，但基本已经尘埃落定了。远低于上学期期末考。
仔细一想，在三周的集训后用一周的时间完全恢复至上学时的状态难度是极高的。而我的那些已经拿到 CSP-S 一等的同学们压根不需要参加开学考——他们已经事实上内定了我所在中学高中部的名额。
于是我突然想起来，我还有两篇游记没写。
一场是 CF Round 969，一场是 ABC369。这两场比赛都对我有着特殊的意义。
总之，在我过初赛之前，我还不能完全投入编程。
到底是为什么呢。
2024/9/22 - Birth in Vacuum
打完初赛，估分。J 组 \(92\) 分，S 组 \(82.5\) 分。理论上进复赛是没什么问题了。
然后晚上打 ABC372。
又要写作业了，烦。
差点忘了今天是我生日。
\(15\) 岁。
我并不快乐。
为什么呢。
2024/9/27 - Reveal
CSP-J/S 成绩提前公布。
J 95.5，S 84.5。进入复赛理论上问题不大。
所以，接下来的一个月，我将全身心投入集训。
游戏，要开始了。
2024/10/6 - Return / NOIP 比赛 \(49\)
分数：\(100+0+20+0=120\)。
T1，由于题目名字叫签到题，所以本题是签到题。具体的，注意到 \(2^{62}>10^{18}\)，\(k\ge 3\) 时可以暴力枚举，所以通过特判和暴力可以拿到除 \(k=2\) 外的所有分数。考虑将暴力根号提取质因数的优化 \(i^2\le x\) 移植到这里变为 \(i^4\le x\)，在最后判断是否是完全平方数即可。最差情况下时间复杂度为 \(O(\sqrt[3]{n})\)。
T2，由于题目名字叫结论题，结合 pdf 特别说明不保证按难度排序，果断放弃。
T3，由于题目名字叫简单题，并且是数学公式，决定直接将暴力打出来并观察特殊性质，然而没有观察出任何东西，于是放弃。
T4，由于题目名字叫套路题，并且想不出套路，暴力实现难度较高，果断转向特殊性质。过掉对应的大样例后开启坐牢模式，并且在接下来的一个小时后除了修掉 T1 使用的 cmath 库的 pow 函数在 \(n\) 太大时出现的错误向下取整问题之外没有任何对分数的提升。然而不幸的是，炸了一个点。
总结：还好 T1 没炸。
2024/10/7 - NOIP 比赛 \(50\)
以后打比赛时不能懒得打暴力，否则分数会爆的。
分数：\(100+50+0+20=170\)。
T1，经过简单的数学分析以及手搓极限数据用时 500ms 成功运行后推断 \(O(n^2m^2k)\) 暴力可过，于是过了。
T2，一眼发现可以转换为长方形内计数，但是不会扫描线，就打了最暴力的 \(O(n^2\log n)\) 加了一点玄学剪枝想碰个运气。结果剪枝没剪干净，再加一个树状数组判断更新答案的可行性就能拿到数据随机的分了。
T3，不会，没打。
T4，发现有性质保证确定风向，于是就打了暴力模拟。本来以为是 \(16\) 分，其实有 \(20\) 分。
总结：暴力能打尽打。
2024/10/8 - NOIP 比赛 \(51\)
对比前两场比赛，向最高分又靠近了一点。
分数：\(0+100+40+0=140\)。
T1，在磕了一个半小时后认为答案取 \(2^{n-m+1}\) 可以拿 \(20\) 分，然后在距离比赛结束 \(10\) 分钟前证伪了，喜提 \(0\) 分。
T2，在蒙完 T1 答案后，想到可以用优先队列和并查集模拟蛇的势力范围逐渐扩张的过程，然后实现了一下，在没有调试的情况下直接通过小样例。用时大概 \(10\) 分钟。然后把大样例丢进去测，发现用时 \(2.3\) 秒，限时 \(3\) 秒，感觉有点悬，加了一点 I/O 优化成功 \(t\leftarrow t-0.6\)，然后就润了。
T3，从 T2 润过来后 ICPC 病犯了死盯着样例想线性解法，然后还把题读错了，去跟龙问了一下才发现是自己语文理解能力过差，然后删了几个字符就拿到 \(40\) 分了。
T4，不会，直接输出 \(0\) 跑路。
总结：看到特殊性质一定要多思考一会。
2024/10/9 - ICPC 比赛 \(7\)
队名：张刘算法。
你问为什么不包含我的姓？答：在这场比赛中，我成花瓶了。
本场比赛使用杭电大“钉耙编程”……算了懒得打了。
AC 题目数：\(7\)。
AC 题目编号：DEFGHJL。
其中，我负责 DH，zl 负责 GL，ly 负责 EFJ。基本上完全符合了赛前我对负责题目类型的预言：
我负责签到，zl 负责数学，ly 负责剩下的。（实际上是数据结构）
刚开始打比赛时，我十分不幸地没有发现签到题，而 zl 十分快速地找到了本场比赛数学题中最简单的一道题。
随后，D 题首 A 出现，我立刻意识到 D 可能是签到题，于是过去看，果然是签到题。
完成代码编写后，第一次运行就通过了样例，提交后 AC。用时 \(8\) 分 \(40\) 秒。
一分钟后，zl 也完成了 G 的编写并通过了样例，提交后 AC，并且是首 A。用时 \(10\) 分 \(52\) 秒。
那么此时 ly 在干什么呢？答：做 F。在 \(15\) 分 \(42\) 秒时，他的代码 WA 了。
于是我走过去问他的思路，他说依靠单调性二分。于是我去看题，愣是没看出哪里有单调性。然后他说，他上界设错了，再交一发。于是又 WA 了。
大概 \(10\) 分钟后，他说，他上界又设错了。然后，他 A 了。用时 \(35\) 分 \(55\) 秒。好在这并不妨碍我们取得本题首 A。
此时我才发现，题目中给出的第 \(i\) 条边边权为 \(i\)，而这保证了插入边可行性的单调性。
随后我们将目光转向 E。看到这题，我和 zl 开始探讨策略，随后我打了一个时间复杂度 \(O(n\log n)\) 的暴力想找找规律。而此时 ly 似乎已经找到了解法，开始打了。然后，在我还在思考如何优化时间复杂度时，他 A 了，用时 \(1\) 时 \(4\) 分 \(1\) 秒。于是我打开他的代码，发现可以用记忆化搜索。
接下来是 L。这道题的思路并不难，但细节处理却消耗了 zl 大量的时间。最终 AC 用时 \(1\) 时 \(26\) 分 \(27\) 秒。那么，zl 和我处理这道题时，ly 在干什么呢？磕 J。
J 是本场比赛竞争最激烈的题目，没有之一。所有人都知道这道题可以使用 01-trie 解决，实现却无一例外地消耗了大量的时间。本题最精妙的部分在于 tag 处理。当时，在吃了两发罚时（MLE+WA）后，我们一致决定打对拍程序。不同于上次，这次我完全没有参与对拍程序的编写，问就是懒得写。然而尴尬的是，ly 的代码包含 C++17 标准的代码，无法在 zl 电脑预装的古董编译器上编译。于是我们通过 note.ms 传送了代码，然后立刻删掉了。接下来就是漫长的对拍。在对拍途中，每次 ly 花十分钟左右的时间完成代码修改，把程序送过来对拍后又会出现新的 hack 样例。在这个过程中，wza 过来炫耀他首 A 的 H。
实际上，在比赛开始看到 H 后，我就想到了一种按照子树节点最小标号值排序后正/倒序赋值的方案，但是当时一是不知道如何证明结论，二是当时没有人 A，不敢打，所以就没打。
wza 过来耀武扬威后，我立刻实现了这个方案，并且终于明白了在一个编号为正序的情况下另一个编号必须为倒序才不会出现不符合题目条件的情况。然后交了上去，A 了。用时 \(3\) 时 \(19\) 分 \(52\) 秒。
在距离比赛还剩 \(1\) 小时的时候，zl 想到了 C 的做法，于是立刻着手实现，并毫不意外地开始了漫长的调试。过了 \(40\) 分钟后，ly 将第 \(10\) 版代码交给了我进行对拍。在长达一分钟都没有 hack 数据出现后，我们提交了代码，于是 AC。用时 \(4\) 时 \(40\) 分 \(7\) 秒。
然后在距离比赛结束 \(2\) 分钟时，zl 说他的状态设计有问题。我们的成绩就此固定了。
最后拿了两个首 A，排在第三名。第一次被带飞。
总结：需要提高注意力和码力。要会设计 DP 状态。要敢写暴力。
2024/10/10 - Chaotic Era
三年前，
饭堂是一缕虚无飘渺的期望，
我在那边，
心在这边。
两年前，
饭堂是一束紧密如亲的牵挂，
身在其外，
心在其中。
一年前，
饭堂是一处嘈杂如市的驿站，
我在里面，
“工作”在外面。
现在，
饭堂是一个避无可避的节点，
肉身在于校内，
心却早已九霄云外。
2024/10/11 - NOIP 比赛 \(52\)
信心赛，但是被各位巨佬吊打。
分值：\(100+80+100+0=280\)。
分值变化：\(100\to 180\to 230\to 240\to 180\to 280\)。
大致解释一下上述分值变化过程。
首先 T1 直接用栈模拟操作就行了，一次运行直接 AC。\(100\) 分 get。
然后看 T2，\(r-l< 10^6\)，感觉是什么神秘暴力优化，但是不会，看到 \(O(r)\) 的线性筛有 \(80\) 分就直接糊过去了，\(80\) 分 get。
接下来是 T3，第一眼以为是什么树链剖分，不会，就打了个 \(O(n^2)\) 模拟，调了 \(20\) 分钟，\(50\) 分 get。
然后发现有链，特判了一下，\(10\) 分 get。
然后不想打了，看 T4。
T4 觉得是非常复杂的 DDP，不想打，而且发现整个机房都会 T3 \(O(n)\) 做法，就开始思考。
于是突然想到用两个数组 DP，一次运行通过小样例和中样例。但是大样例会 RE。为什么？
然后拿 gdb 出来 r 了一下，告诉我是在一次调用的时候 RE 的。栈溢出。但是忘了编译指令？怎么办？问龙。然后龙搜索的时候突然想到了，然后回去加上了，0.5 秒，正确。
感觉有点悬，assert 了一下有没有多余的递归调用，确定没有之后上了个快读，成功 \(t\leftarrow t-0.4\)，然后润了。
最后 T4 也没瞪出来。
总结：要提高注意力。
2024/10/12 - NOIP 比赛 \(53\)
好像一堆同学挂分了，但是我没挂。比较开心。
总分：\(100+100+12+10=222\)。
分值变化过程：\(0\to 30\to 100\to 100\to 200\to 212\to 222\)。
看到 T1 时被数据范围误导了想打莫队，结果在处理删除时抓耳挠腮。然后看到两边的同学都在打可持久化线段树才发现可以这么做，然后就删掉重打了。
打完用了大概半个小时，然后一直出问题，出了一个半小时问题。中间心态崩过一次想打个 \(O(nm\log n)\) 暴力了事，最后改了一种写法过了，不知道为什么。总之过掉后已经没了两个小时，信心全无。
接下来看 T2，感觉是一些非常复杂的规划。做不出来。然后在那瞪了五分钟，想着死马当活马医就随便搓了个贪心顺序就打了，打的过程中拿着小样例手模了一下发现是对的，于是继续打。打完之后过了样例，然后测大样例就不出意外地 TLE 了，两分钟都不出结果。
怎么办呢？突然注意到一种货物塞满整个电梯时会造成大量的重复循环，于是用了点位运算压掉了，然后继续测大样例。0.9 秒。然后 diff，woc，输出怎么是空的？过了？？？然后继续测后两个，0.98 秒，也过了？？？？？
总之这个时候又找回了一点信心，为了更稳一点加了个快读，然后成功 \(t=t-0.5\)。Fast I/O NB。
然后看 T3，暴力就是大模拟，懒得打了，直接处理前三个数据了事。
最后看 T4，显然不可做，直接输出理论上界 \(nk\) 然后坐牢。
期望分数 \(100+0+12+0=112\)，因为当时完全不相信 T2 贪心是对的，然后测出来是对的，T4 也有一个数据卡到了理论上界，然后得了 \(10\) 分。
看着似乎还不错？
2024/10/13 - Luogu SCP-J/S
J AK，S \(184\)。
然而 J 并没有用。
2024/10/14 - NOIP 比赛 \(54\)
挂分了。
得分：\(100+6+10+52=168\)。
分数变化过程：\(100\to 152\to 158\to 168\)。
T1 在看到题的那一刻就知道是拆位了，然后直接切掉。
然后先看 T4，因为 T4 是个操作题，而且有很多部分分。
首先发现 T4 是把一个序列逐渐向上拉平的过程，然后手写链表把前 \(52\) 分拿了。
接下来看 T2，在那里瞪了一个小时都不知道怎么做，然后突然发现 \(a_1=k\) 有 \(6\) 分，然后就打了。
最后看 T3，直接上手大暴力，过了小样例，期望 \(35\) 分，然后挂了。
离比赛结束还有一段时间，突然意识到 T4 还有剪枝的空间，于是继续实现，跑大样例的时间快了一点，然而还是没拿到值随机的部分分。
总结：打暴力时注意暴力的正确性。
2024/10/15 - NOIP 比赛 \(55\)
你绝对不会相信一场正常的比赛可以通过打最低档暴力获得最高的分。
然而，这场比赛做到了。
得分：\(100+50+0+0=150\)。排名第一。
T1，看到题目，又想起前天刚打的 ARC185，想起最后一道题的解法用到了欧拉函数，然后发现用欧拉函数可以在不使用容斥的情况下解决这道题。于是过了。
T2，看到题目，觉得没戏。但是发现两边的同学都在打 cdq 分治。不会，怎么办？于是在比赛结束前 \(10\) 分钟打了个朱刘算法，但是无济于事，还是 \(50\) 分。
T3，看到题目，感觉是 CF 经典套路，但是不会，打了个链，结果没吃到。
T4，看到题目，红温，直接放弃，输出 \(-1\)，得到空气。
总结：DP，分块和分治是三座大山。
2024/10/16 - NOIP 比赛 \(56\)
自闭了。
总分：\(100+32+0+56=188\)。
T1，对着样例盯了整整半个小时，然后发现是大分讨，然后过了。
T2，不会，只会 \(x=1\)，然后乱调式子过了 \(x=1\) 的大样例就没管了。
T3，不会，直接 shuffle 碰运气，显然没戏。
T4，还是不会，用了点奇技淫巧（ST 表 \(O(1)\) 最值+gp_hash_table 卡常）然而还是只有暴力分 \(56\) 分。
大后天得拿多一点分以保住 B 班的位置。
总结：这是 OI 赛制，不是 ICPC 赛制，试错没有成本，多猜几个结论可能就猜出来了。
2024/10/17 - ICPC 比赛 \(8\)
再次被队友带飞。
A \(7\) 题。
AC 编号：ABCEFGI。
完全自主完成：\(0\) 题。
一血：AFG。
队长：JT。
队名：如果周乐就会染上于于蒸。
队员：JT，ZL，RS。
比赛开始后，jt 马上发现了 G 是签到题，并且极速推出结论让我进行实现。然而我发现他没有说平局的情况。但是 jt 认为没有平局，于是我继续实现，然后过了样例，jt 说可以交，于是交了，之后过了。
G. 小猫钓鱼，AC，思路：JT × RS，实现：RS，用时：\(14\) min \(28\) s，一血。
与此同时，ZL 正在实现 E。他非常快地完成了实现，然后交了，AC。
E. 怪物猎人，AC，思路：ZL，实现：ZL，用时：\(23\) min \(6\) s。
接下来看到 F。看到题面后我提出一个猜想，那就是合并严格不优。于是和 JT 交换意见后决定直接打完全背包，然后 JT 说我的做法周了，需要调整分子，所以就没继续打，直到将近 \(10\) 分钟后 JT 在群里告诉我 A 了。
F. 融合矿石，思路：JT × RS，实现：JT，用时：\(40\) min \(51\) s，一血。
接下来陆续发现 B 和 C 都有人过了，非常慌张，但是因为自己菜的一批所以完全没有思路。
于是我盯着 A 题看，突然发现了华点一个神奇的事情，那就是 \(6^3=216\)。而且 \(k=3\)，于是合理猜测每个位是互相独立的，而且根据小学数学和拆贡献易得每一个子树内最优的方案都是一半 \(1\) 和一半 \(0\)，其中如果子树大小是奇数那么翻转的方案也是最优的。然后搓了一份看着很有问题的代码发给 JT。然后 JT 就交了，他说他看着没什么问题。确实 WA 了。然后我开始画图，接着发现 JT 又交了一发，是把子树转移过程中的特判给放到循环外面去了，还是 WA。但是我实在想不出来了，就去看其他题。然后 JT 说，他 A 了。
A. 树异或价值，+2，思路：JT × RS，实现：JT × RS，用时：\(2\) h \(5\) min \(41\) s，一血。
与此同时，ZL was working hard solving debugging his code of B. 他打了整整 \(130\) 行，然后一遍过了。
B. 树上询问，AC，思路：ZL × JT，实现：ZL，用时：\(2\) h \(38\) min \(49\) s。
接下来，JT 和 ZL 都被 I 硬控了，原因是求凸包一向是 ICPC 特有毒瘤题，仅次于大模拟，更何况这题还是多个凸包。在他们的通力合作下，他们终于在吃掉 \(12\) 发罚时的情况下 A 掉了这道题。
I. 长期素食，+12，思路：JT × ZL，代码：JT × ZL，用时: \(4\) h \(13\) min \(17\) s。
那我在干什么呢？调 D。没错，由于前面的题目都由团队中另外两人负责，攻下这道模拟题的众人自然就落到了我的身上。然而我糖分过高，选择了一种非常复杂的写法，既无法保证正确性也有极高的调试难度。
在这种吃力不讨好的情况下，我没有在赛时成功通过此题。
而在比赛结束前 \(10\) 分钟，JT 通过了 C。
C. 黑洞合并，+1，思路：JT，实现：JT，用时 \(4\) h \(48\) min \(22\) s。
结束了。
总结：被大佬带飞，会同时产生愧疚、骄傲、嫉妒、羡慕的情感。
2024/10/19 - NOIP 比赛 \(57\)
痛，太痛了。
集训第一次挂分。
得分：\(100+12+5+40=157\)。
T1，看到题目后直接切掉。
T2，不会，于是手玩发现和位运算有关系，于是打 \(O(n^2)\) 的暴力 DP。大样例全过。然后在比赛结束前半个小时突发奇想觉得可以用 bitset 优化空间，结果初始化时有一个位置少初始化了，导致 \(64\to 12\)。
T3，不会，打暴力。
T4，不会，暴力剪枝。
总结：在距离比赛还剩 \(7\) 天时给我这么一锤子算是唤醒了我悲痛的记忆。
2024/10/21 - NOIP 比赛 \(58\)
更痛了。
集训第二次挂分。
得分：\(50+40+5+0=95\)。
T1，看到题目后想到显然的贪心思路，然后写出来，大样例全过，然后去看了一下大样例的规模，看起来很有强度，就没管了。
T2，看到题目后感觉能推，于是将整场比赛中的 2.5h 全部花在了这道题上，结果一无所获，直接打暴力走人。
T3，看这题时离比赛结束只有 \(20\) 分钟了，直接打 \(n=1\)。
T4，不会。
总结：明天至少得有 \(60\) 分。不要相信出题人。就算出题人是三体人，他们也早已学会了隐瞒。
2024/10/22 - NOIP 比赛 \(59\)
这次没挂分，但是很痛。
得分：\(100+24+0+0=124\)。至少不用去 C 班了。
T1，打表直接发现规律，切。
T2，将暴力打出后想到了树链剖分+矩阵乘法的解法，然而很不幸地没有调出来，于是将暴力交了上去。这道题耗费了我整场比赛的时间。
T3，看了，知道最优策略是选最左侧的向右移，然而为了冲 T2 正解放弃了。
T4，看了，不会。
总结：不要对自己的思维能力抱有任何的幻想。
2024/10/23 - NOIP 比赛 \(60\)
无话可说。
得分：\(100+0+40+20=160\)。评价为出题人缺乏同理心。哦，他 NOI 金啊，那没事了。自己太菜导致的。
T1，把题面看错了一个字母，然后打了出来，测了样例，错了，于是再看一眼，爆炸了，于是将原来的思路进行微小的调整，发现理论可行，于是开打，打完后距离比赛开始 \(30\) 分钟，然后开始漫长的调试，中间又是忘了加一又是没处理 \(0\) 又是把乘号打成加号，好在最后还是 A 了，总用时 \(1\) 时 \(20\) 分钟。
T2，当时 cen 出去了一趟跟整个 B 班的人说这道题 A 班都一群不会的，于是放弃了，随便瞪了一个样例输出 \(2^n\) 走人，结果自然是没分的。
T3，觉得可以整一个类似拉链的优化暴力，结果等到距离比赛结束 \(30\) 分钟时才发现假了。于是把原来的无优化暴力交了上去。
T4，好在在开始搓 T3（我认为的）正解之前先把 T4 的暴力打了，不至于一分不得。
总结：在开始搓（自己认为的）正解之前最好先把其他题目的暴力打了，因为这样做这道题的时候可以更踏实，不用分心想其他题，而且可以获得更高的稳定性。
2024/10/24 - ICPC 比赛 \(9\) NOI Linux 基本操作
今天的比赛区分度太低了，写一点有用的。
今天没有总结。
首先，你需要学会创建文件。
在终端中，输入以下命令：
touch foo.cpp
可以创建一个名为 foo.cpp 的文件。
为了编辑这个文件，你需要一个代码编辑器。
NOI Linux 中，有两种较好的编辑器，建议零基础用户使用 Visual Studio Code。首先，需要通过 cd 命令将终端的工作目录移动至代码所在的目录。
cd 命令有以下三种调用格式：
cd /absolute/path/to/file
cd relative/path/to/file
cd ~/relative/path/from/home/to/file
其中，第一种调用方式的参数首位为 /，输入绝对路径。第二种调用方式的参数首位即为文件夹名字的一部分，要求输入以当前目录为根目录的路径。第三种调用方式本质上为第一种调用方式下要求导向 /home/username 目录的简写。其中，~ 指代 /home/username。
在你瞎 jb 乱搞后终于将工作目录设为代码所在的目录后，你需要使用上面提到的编辑器打开文件。在终端中输入如下指令：
code foo.cpp
你的面前会出现一个窗口，里面展示 foo.cpp 文件的内容。你可以使用它编辑你的代码了。
现在你完成了代码的编写，希望运行一下。此时，不要使用代码编辑器内置的运行，效果不直观，而且配置麻烦。你可以通过如下命令编译你的代码。
ulimit -s unlimited
g++ foo.cpp -std=c++14 -O2 -Wall -Wextra -o foo
其中，第一条指令的意义是解除栈空间限制。注意，如果你重新打开终端，为了重新解除栈空间限制，你需要再次运行第一条指令。
但是，下面的命令有点长，有些人可能会有记忆上的困难。你可以通过以下的办法方便地记下这个编译指令：
g++是GNU C++ Compiler的缩写。- 告诉
g++你要编译什么文件。在这里，它叫foo.cpp。 - 告诉
g++你需要用什么标准编译文件。按照 NOI 系列赛的标准，你需要使用 C++14。 - 告诉
g++你需要用什么方式优化代码。按照 NOI 系列赛的标准，你需要使用 O2 优化。 - 告诉
g++你需要知道一切你不应该做的行为。Wall可以被理解为Warn All，警告全部的风险行为。 - 告诉
g++你需要避免一切你可能不应该做的行为。Wextra可以被理解为Warn Extra，警告全部的可疑行为。 - 告诉
g++你需要指定程序的名字。-o可以被理解为output，即输出文件的名字。一般情况下，-o后的文件名一般取代码文件名去掉后缀名的结果。
做完上面的事情后，你得到了一个叫做 foo 的程序。但是，怎么运行它？此时，在终端中输入如下命令：
./foo
没错。就这么简单。其中，. 指代当前目录，强调你需要运行这个目录下的一个程序。
在没有打开文件读写的情况下，运行上述命令后，foo 程序就会等待你的输入。只需要将题目给出的输入数据粘贴至终端内，程序就会给出它的输出。
有时候，如果你不想开启文件读写，又不想将巨大的输入数据粘贴进终端，你可以这么写：
./foo < foo.in > foo.out
其中，小于号后的文件的内容会作为输入数据输入程序，并且输出会被写进大于号后面的文件里。
为了更为精准地计算你的程序的运行耗时，你可以使用以下的指令：
time ./foo
time 命令会计算你的程序的用时并输出到标准错误流中。也就是说，不管你有没有输出重定向，你总是能在终端看见你的程序用时。
如果你只是想要在 NOI Linux 里面检验你的程序运行效率，那么上面的东西已经足够了。事实上，考场上与 Linux 强相关的操作并不多。如果你在 Windows 里也使用命令行编译程序，那么迁移学习的成本并不大。
但是，如果你想在 NOI Linux 中完成整场比赛，你还需要这些东西：
比对文本。格式如下：
diff foo.txt bar.txt
这个指令会输出两个文件的不同之处。如果这两个文件的内容相同，这个指令的输出将为空。
创建文件夹。格式如下：
mkdir directory
这个指令会创建指定名称的文件夹。
快速输出文件内容。格式如下：
cat foo.txt
该指令会在终端输出指定文件的内容。
重命名/移动文件/文件夹。格式如下：
mv foo.txt bar.txt
mv foo.txt foo
该指令有两种调用方法。若上述指令的参数二在目前目录下不存在，那么该指令的用途为重命名参数一指定的文件或文件夹。否则，上述指令的意义为将参数一指定的文件或文件夹移动至参数二指定的文件夹内。
复制文件/文件夹。格式如下：
cp foo.txt bar.txt
cp foo.txt foo
该指令有两种调用方法。若上述指令的参数二在目前目录下不存在，那么该指令的用途为将参数一指定的文件或文件夹复制一份并命名为参数二的内容。否则，上述指令的意义为将参数一指定的文件或文件夹复制至参数二指定的文件夹内。
2024/10/25 - NOIP 比赛 \(61\)
NOI 金出的良心赛，但是数据用脚造。这么出信心赛会让人生理不适的。
预估得分：\(100+40+25+12=177\)。
实际得分：\(100+40+100+12=252\)。
T1，感觉十分神必，于是在脑子里一阵 yy 后得出了最多只有一种颜色的球能做到鸠占鹊巢的结论，于是过了。
T2，做完 T1 后觉得可以 \(O(k^4)\)，但是做分讨的时候生理不适，于是就放弃了，打了 \(O(n^4)\) 暴力。
T3，做完 T2 后惊喜地发现 T3 是操作题，但是一看数据范围 \(O(n^2)\) 只给 \(15\) 分，谔谔。于是花一点时间打了一个用链表优化的暴力，然后过了小样例。然后不想测大样例了，因为在打 T3 的时候电脑死机了 \(3\) 次（三回啊三回）靠 Ctrl Alt SysRq REISUB 大法才救了回来。然后感觉屏障和陨石的区间大小都是 \(1\) 的部分分能打，于是实现了，之后发现竟然没有这个性质的大样例，一阵 mmp 之后自己造了一个小得一批的数据然后 WA 了，才发现了问题，要不然就少 \(10\) 分了。然后打了 T4 \(8\) 分暴力之后回来测了一下大样例，惊讶地发现最大样例用时仅有 0.08s，在再三确认自己没有出现幻觉后认为最大规模数据额外保证数据随机生成，于是放弃了对其他部分分的实现。
T4，一眼不可做，于是打了一个 \(8\) 分暴力。比赛快结束的时候发现 \(m=c=1\) 可以 \(O(n)\) 推过去，于是打了，多了 \(4\) 分。
总结：拥抱不确定性，明天考场加油。
2024/10/26 - CSP-J/S \(2024\)
见这里。
2024/10/29 - Waiting and Waiting, as the Knowledge Slowly Fading
CCF 精心地将成绩/代码公布日期放在了期中考后一天。
也就是说，我们必须参加期中考。
烦。政治已经连一个知识点都记不下来了。数学的恢复速度倒是不慢。
不过现在心能静下来了，可以试着打一些之前不会的东西，比如说 Kruskal 重构树。说来也是挺奇妙的，当时做 NOI2018 的归程的时候因为不会 Kruskal 重构树所以直接写了一个可持久化并查集。结果，今天做了 ONTAK2010 的 Peaks 加强版才知道有些题硬要用可持久化并查集是会出人命的。
所以我也算是在没学 Kruskal 重构树的前提下了解了 Kruskal 重构树的原理。
关于 DP，实际上在接触 DP 到今年的 CSP 前不久我都认为 DP 是我始终无法攻破的知识点。直到在那场梦熊周赛中我独自推出了 \(3\) 维的暴力 DP 后我的 DP 能力才出现了爆炸式的增长，也间接决定了我能在 CSP-S 赛时想到 T3 的 \(O(n^2)\) DP 解法。虽然不是满分，但也是一等的重要保障。
感觉离退役不远了，尽量多写点吧。
2024/11/1 - 仓颉造代码
今天开新坑。见这里。
