0 写在前面
浓绿万枝红一点,动人春色不须多。——王安石
让·巴蒂斯特·约瑟夫·傅里叶男爵(法语:Jean Baptiste Joseph Fourier,法语发音:[ʒɑ̃ batist ʒozɛf fuʁje];1768年3月21日-1830年5月16日),法国数学家、物理学家,提出傅里叶级数,并将其应用于热传导理论与振动理论,傅里叶变换也以他命名。他被归功为温室效应的发现者。
1 基本介绍
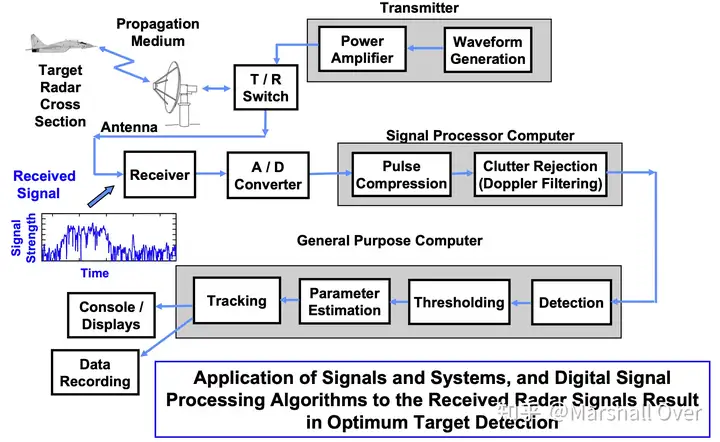
信号和系统以及数字信号处理算法:在接收雷达信号中的应用实现最佳目标检测。
2 信号处理
信号处理:对信号的处理、分析和解释。
信号处理包含:自适应滤波/阈值;频谱分析;脉冲压缩;多普勒滤波;图像增强;自适应天线波束形成;许多其他非雷达技术(图像处理、语音处理等)。
信号处理:数据的收集、存储和转换。模拟和数字信号处理;通常需要大量的处理“马力”。
2.1 连续信号
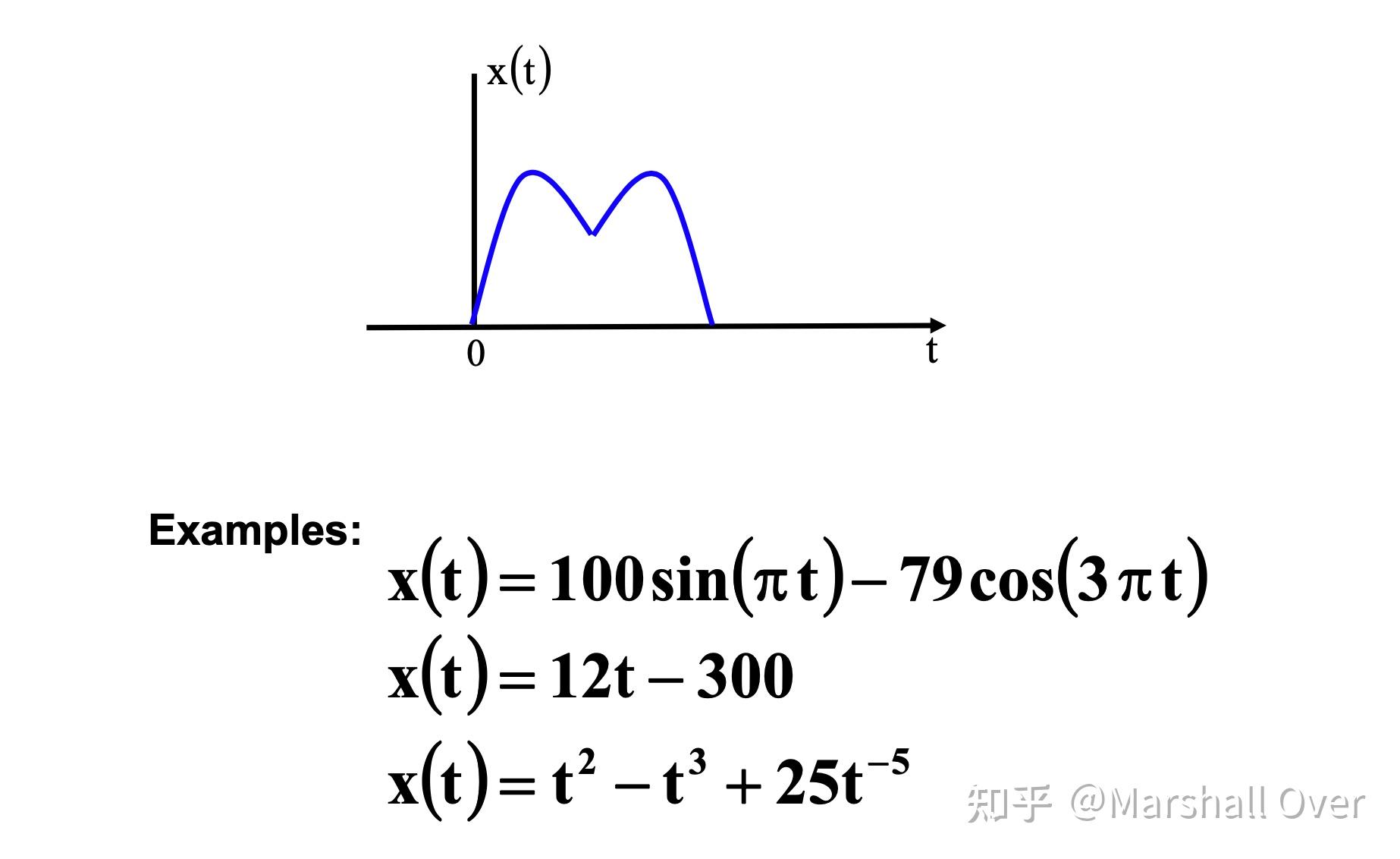
连续时间信号:在时间上连续的信号。
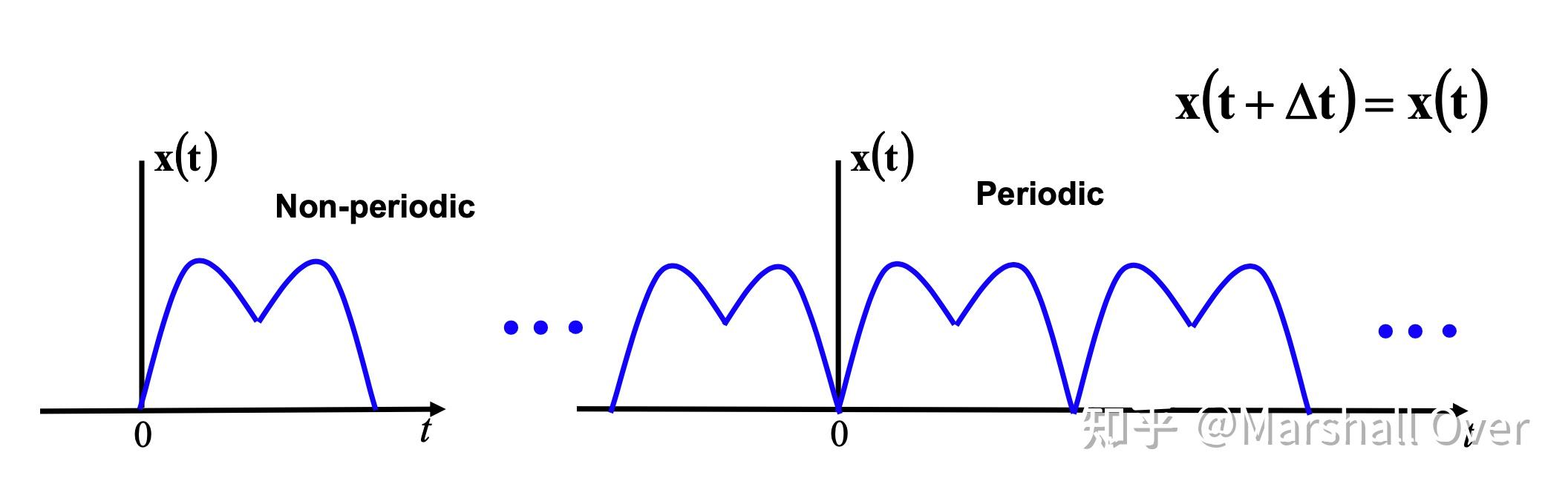
连续时间信号的类型:周期性或非周期性。
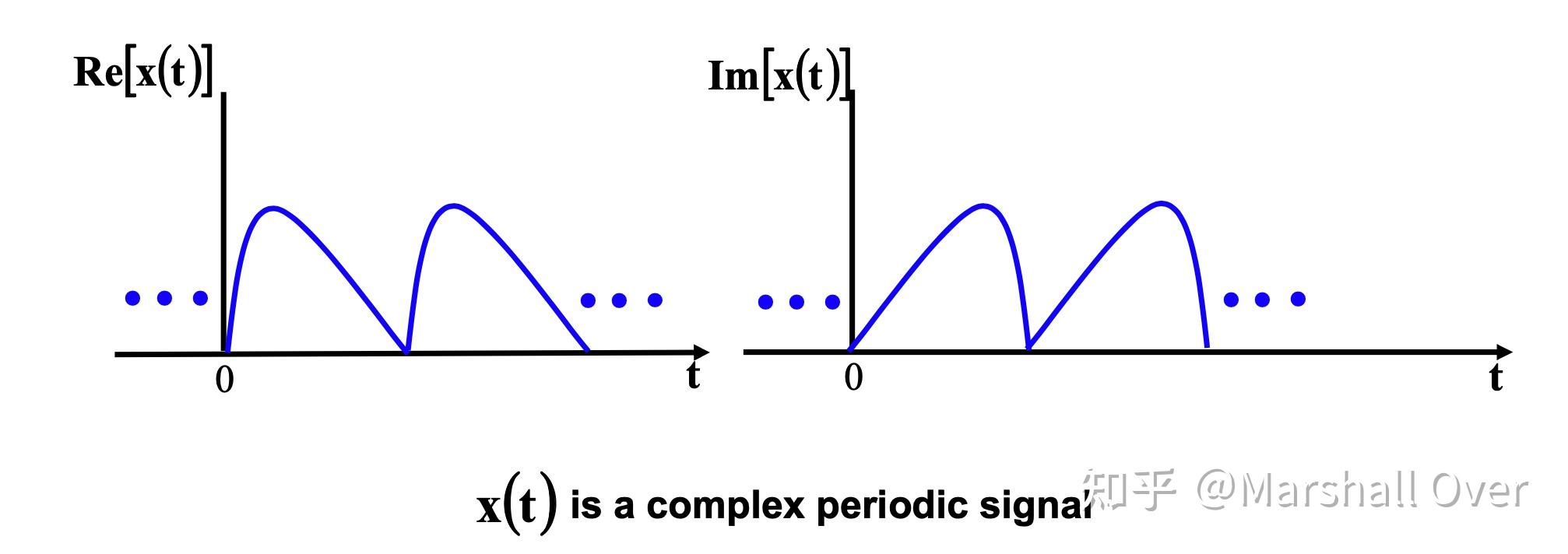
连续时间信号的类型:周期或非周期;实信号或复信号:雷达信号为复信号。
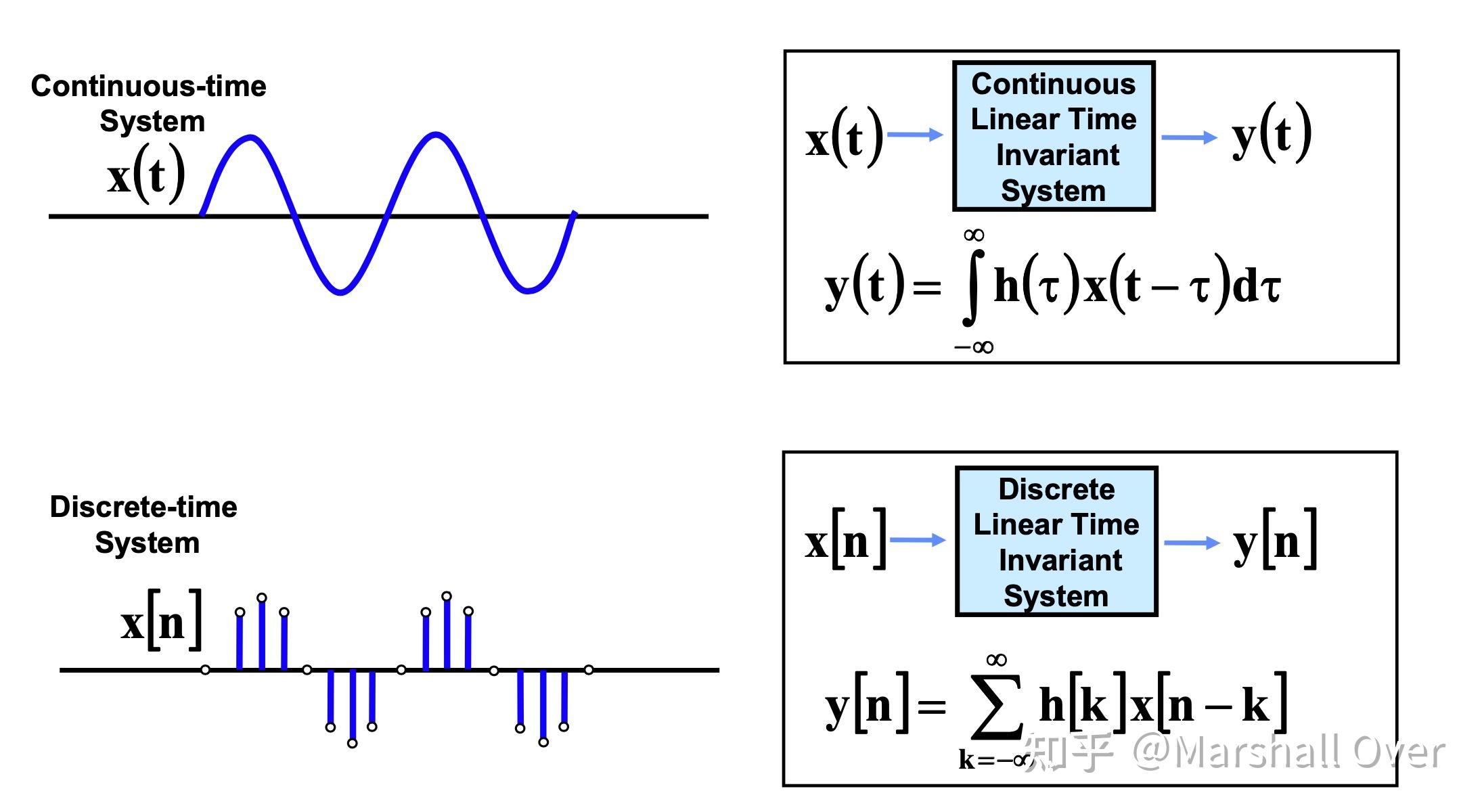
连续、线性、时间不变系统:
连续:输入和输出都为连续时间信号;
线性:\mathbf{T}[\alpha x_1(t)+\beta x_2(t)]=\alpha y_1(t)+\beta y_2(t);
时不变:如果输入的时间偏移,导致输出的时间产生同样的偏移。
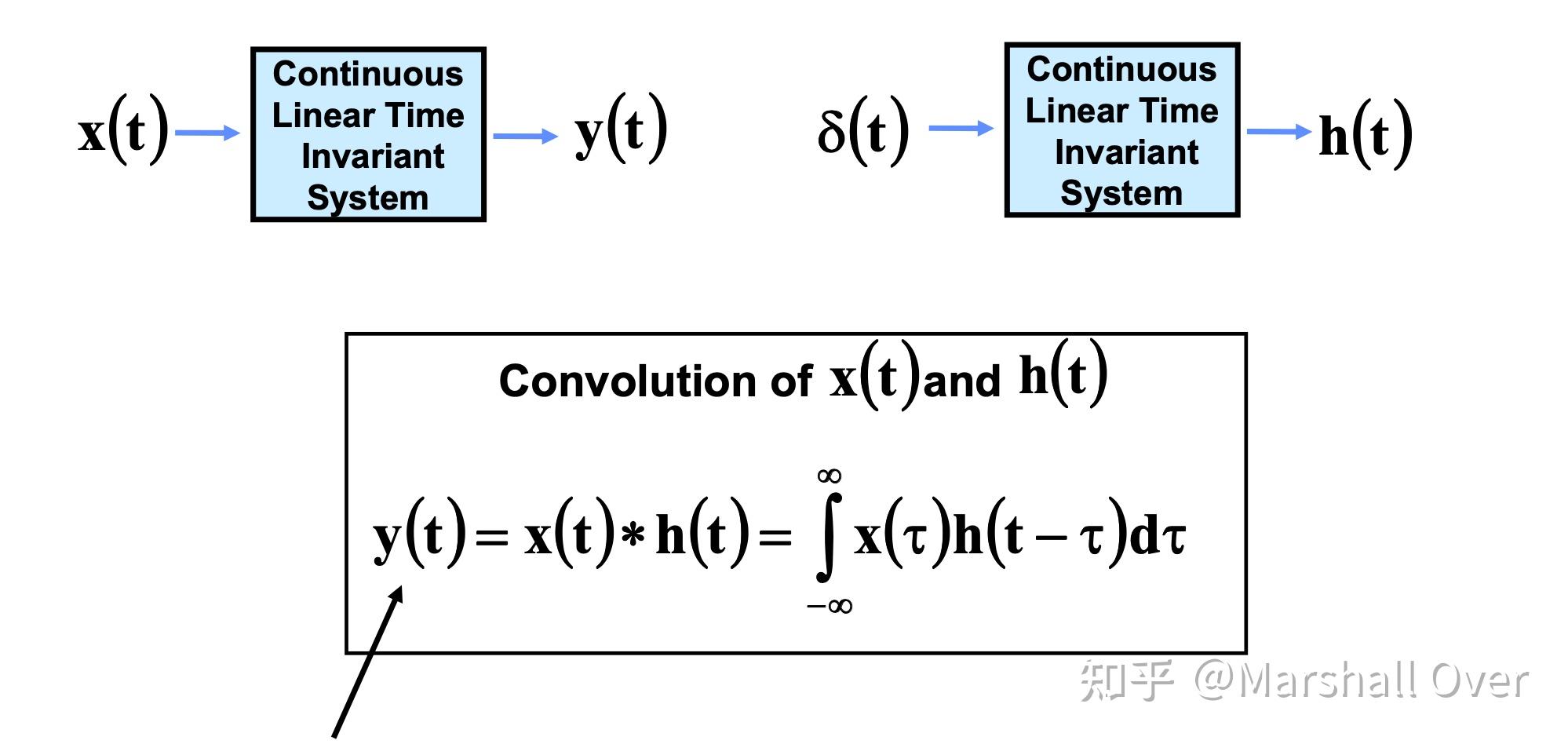
线性时不变系统(Delta Function):脉冲响应h(t)是当输入为\delta(t)时系统的响应。
两个函数的卷积定义:这里不在介绍了,可参考:
系统输出:任何连续时间、线性、时不变(LTI)系统的输出是输入 x(t)与系统h(t)的脉冲响应的卷积。
为什么不使用模拟传感器和计算系统?
2.2 采样数据与离散时间系统
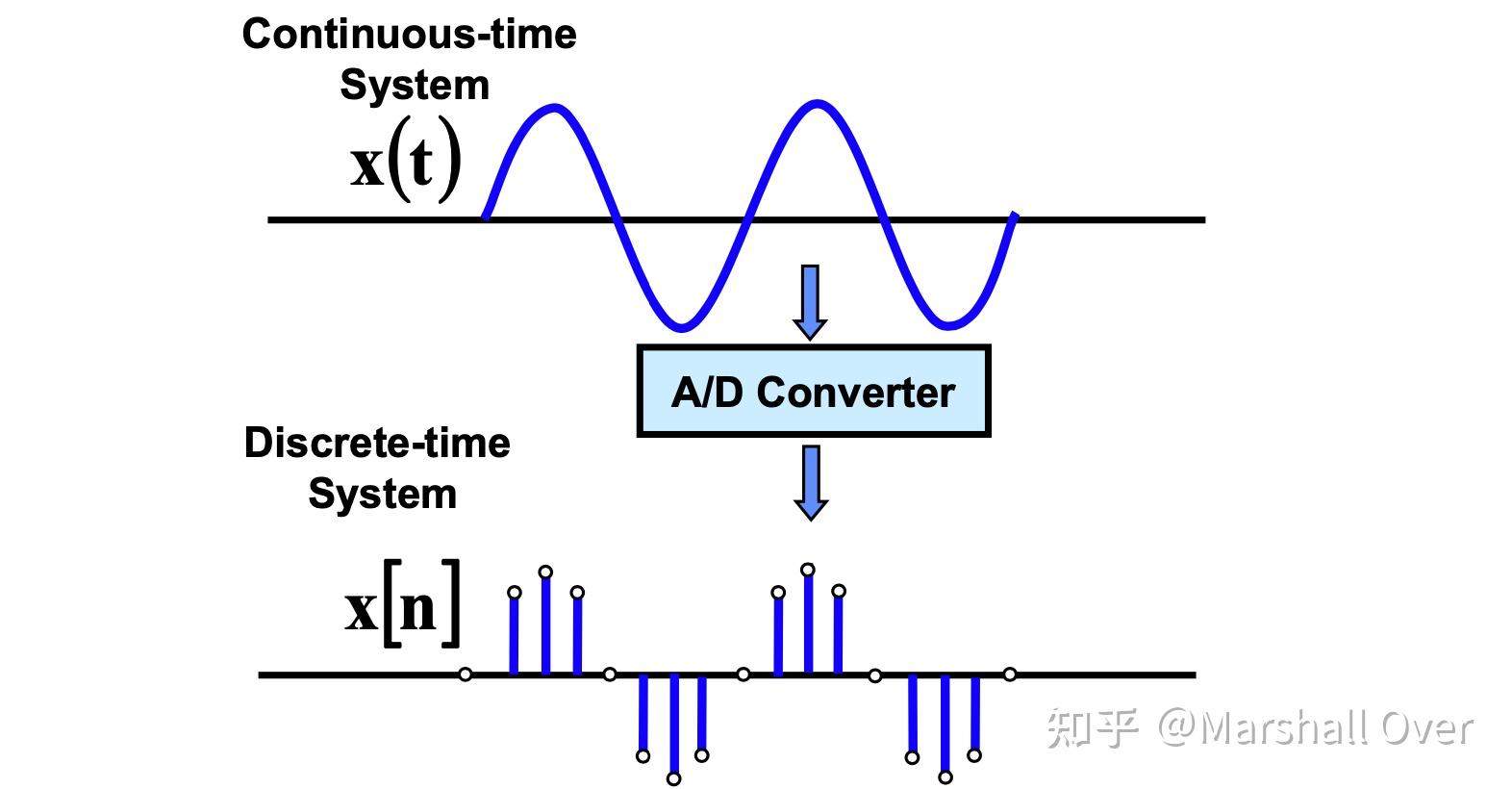
采样数据系统:数字信号处理处理采样数据;数字处理不同于处理连续(模拟)信号;数字采样是通过“采样保持”放大器和“模数”(A/D)转换器获得的。
波形采样:采样将连续信号转换为数字序列。
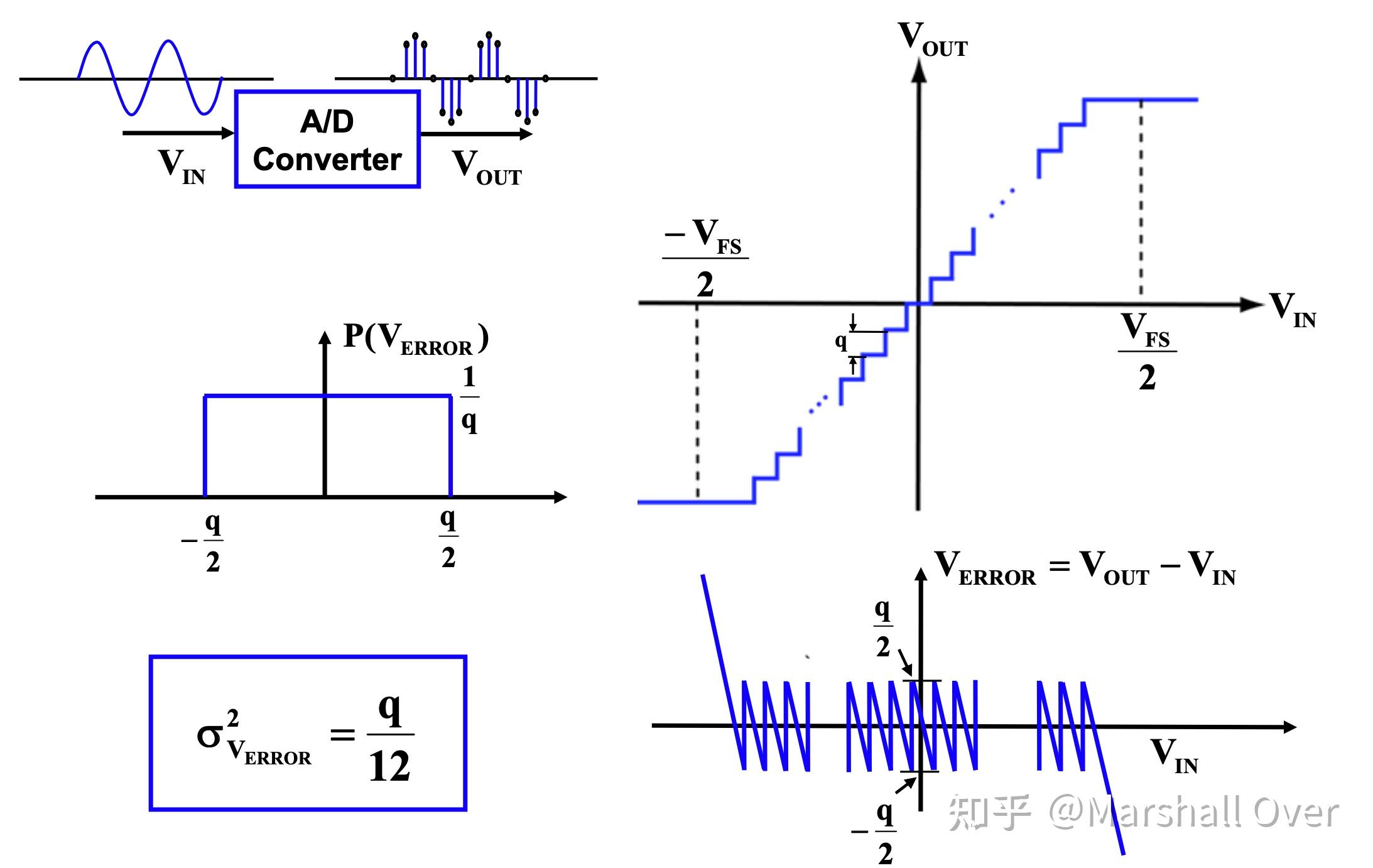
理想的模数(A/D)转换器:
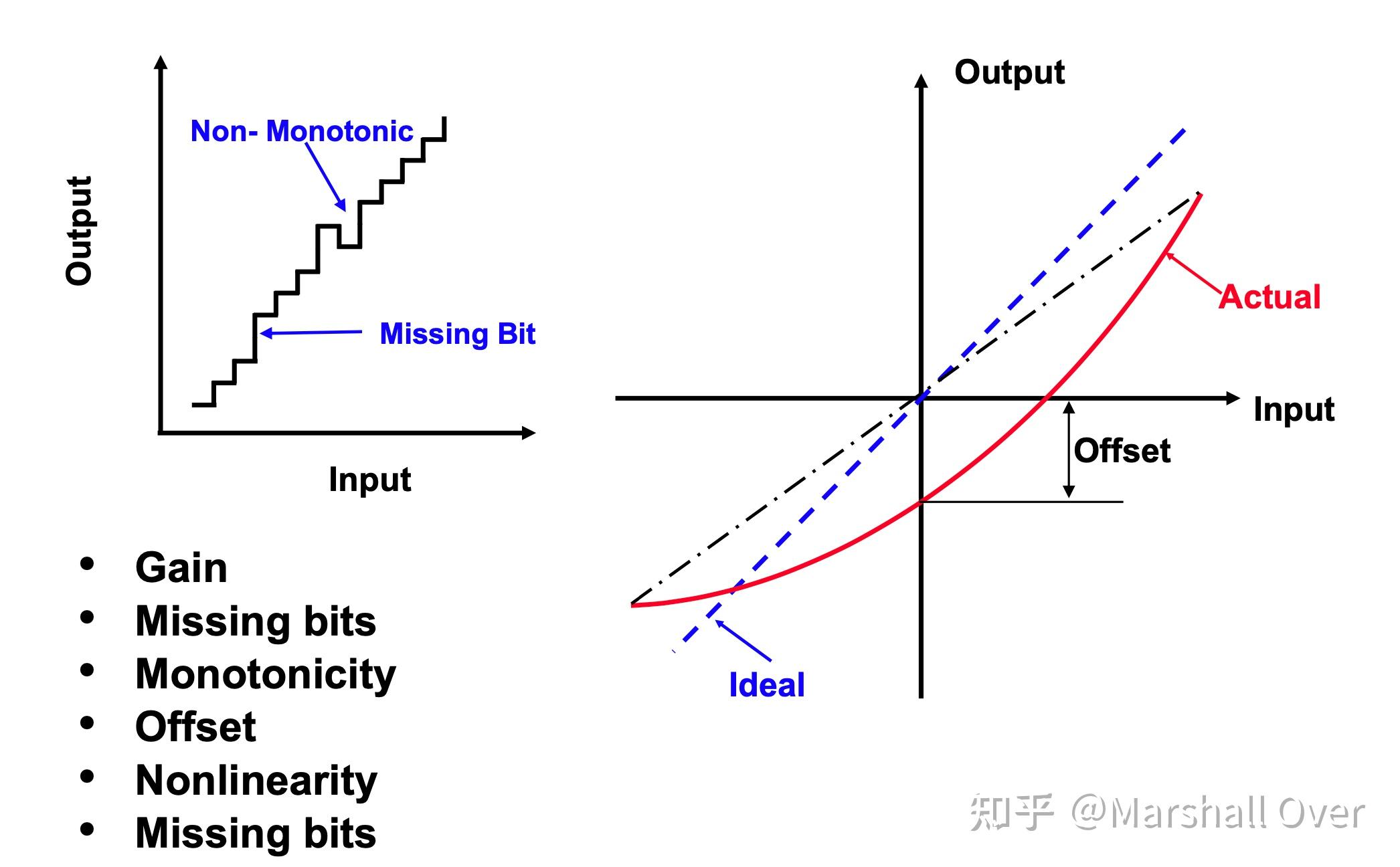
A/D转换器的“非完美性质”:增益;缺失位;单调性;偏移;非线性。
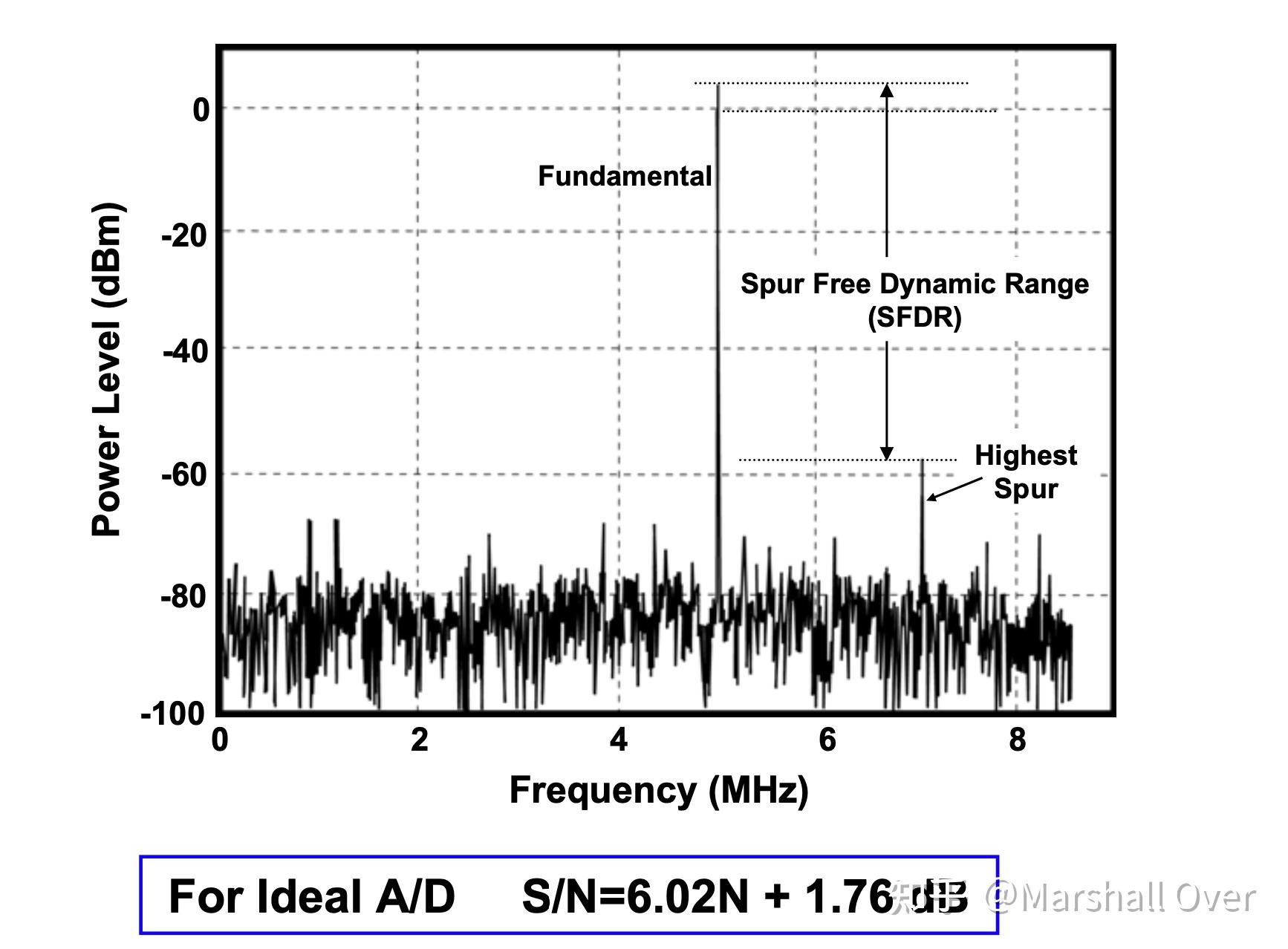
A/D转换器测试:
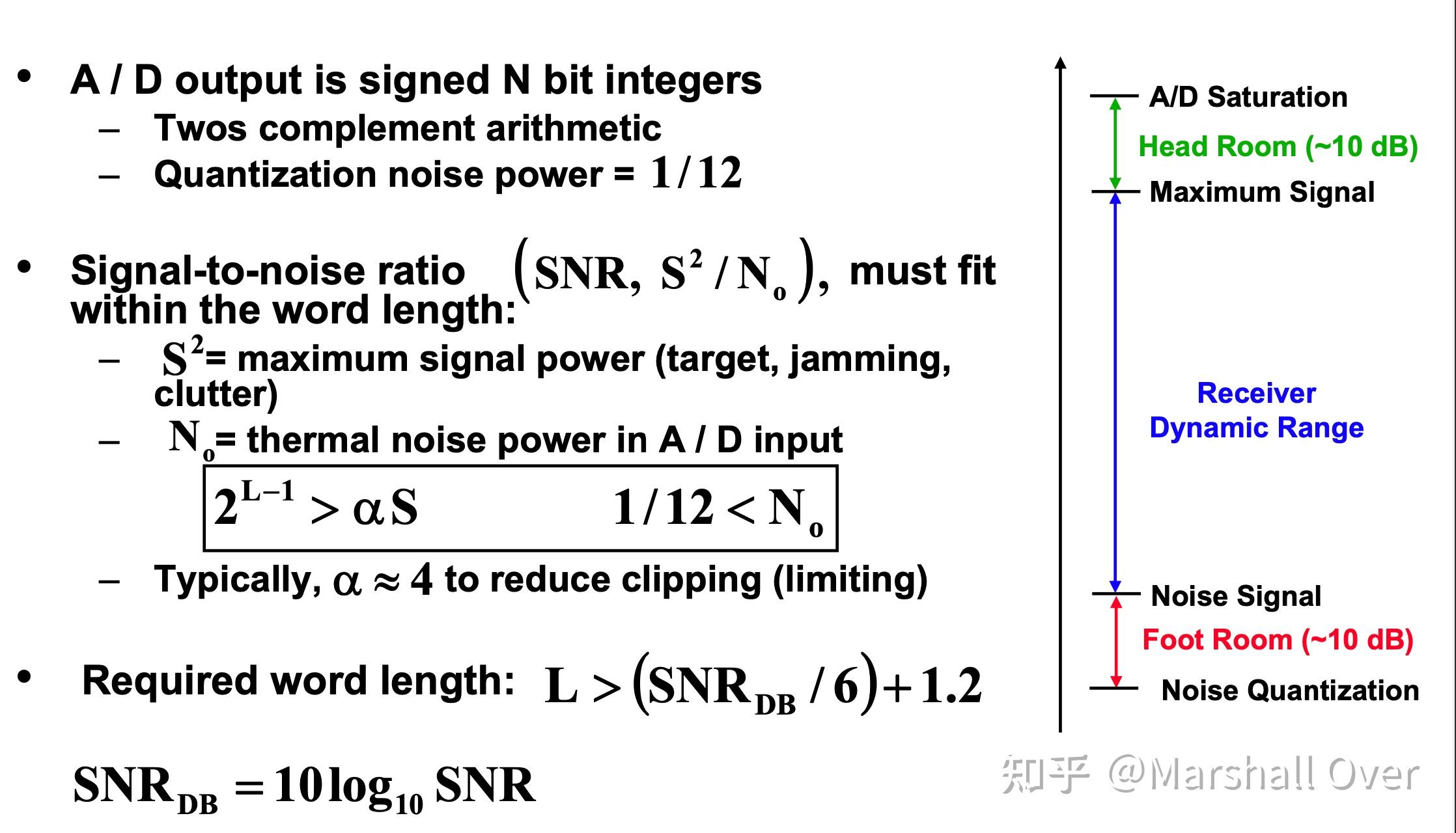
A/D位数:
采样-概述:
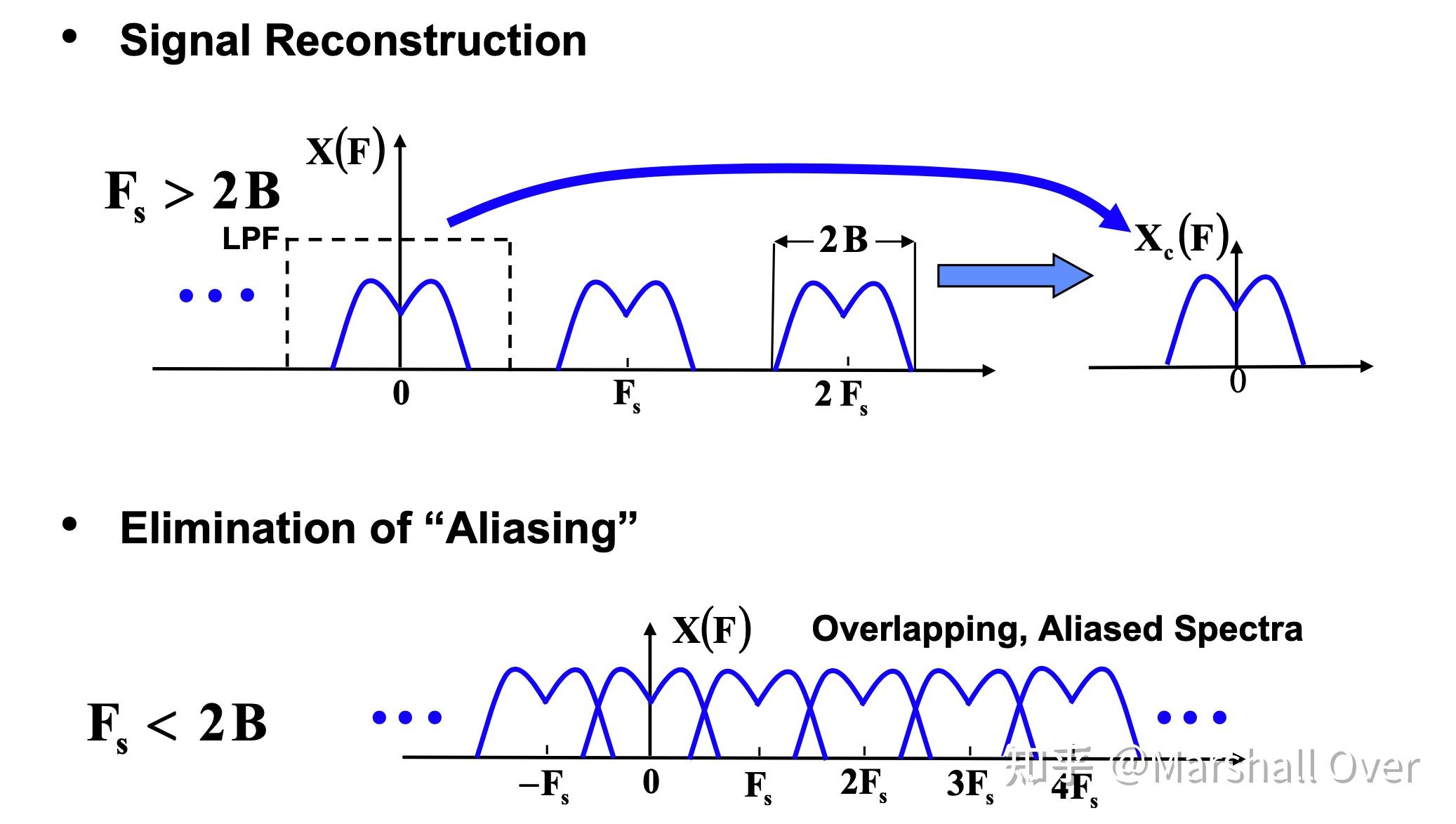
信号采样问题:信号重构和消除“混叠”。
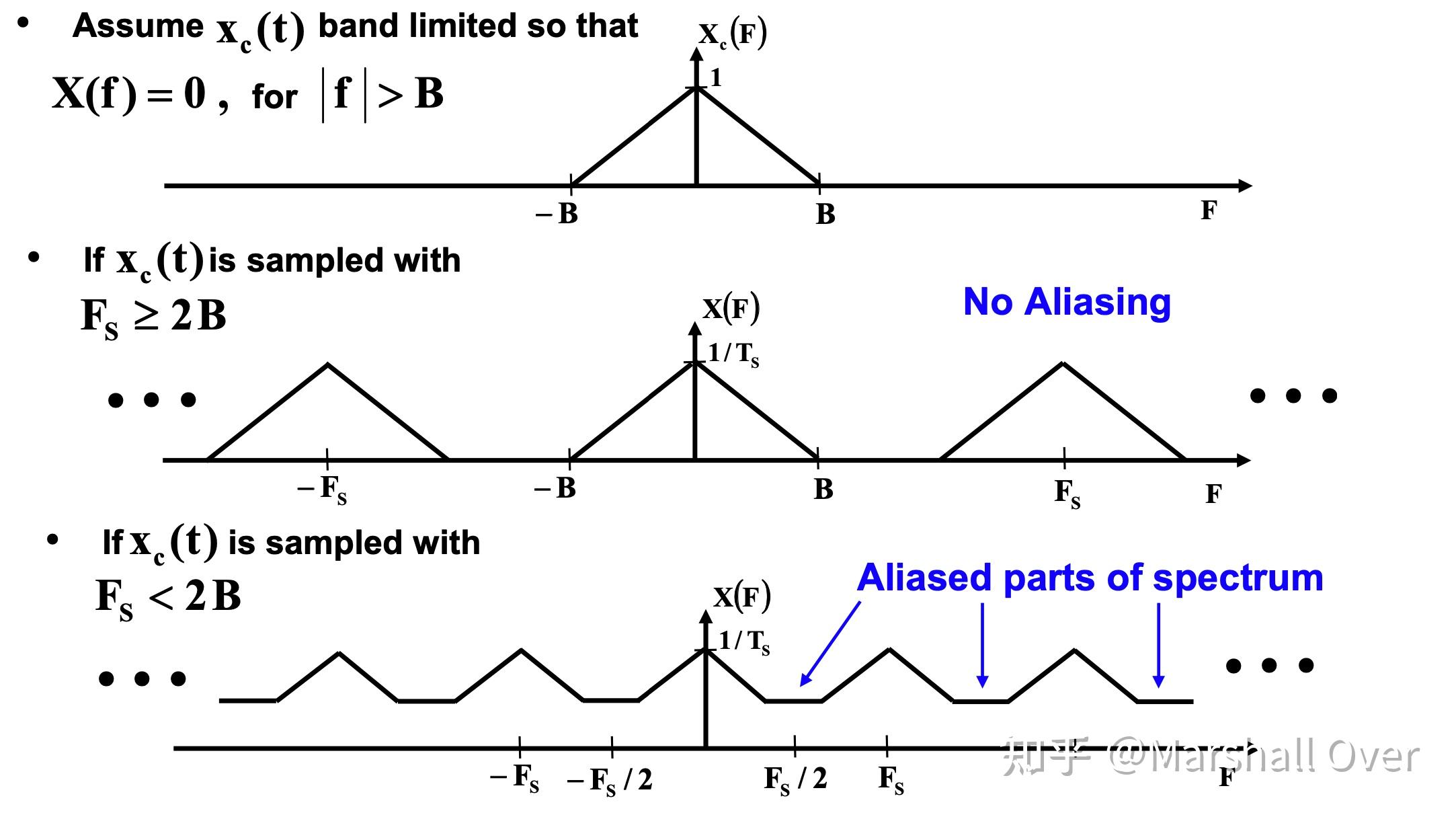
采样定理:
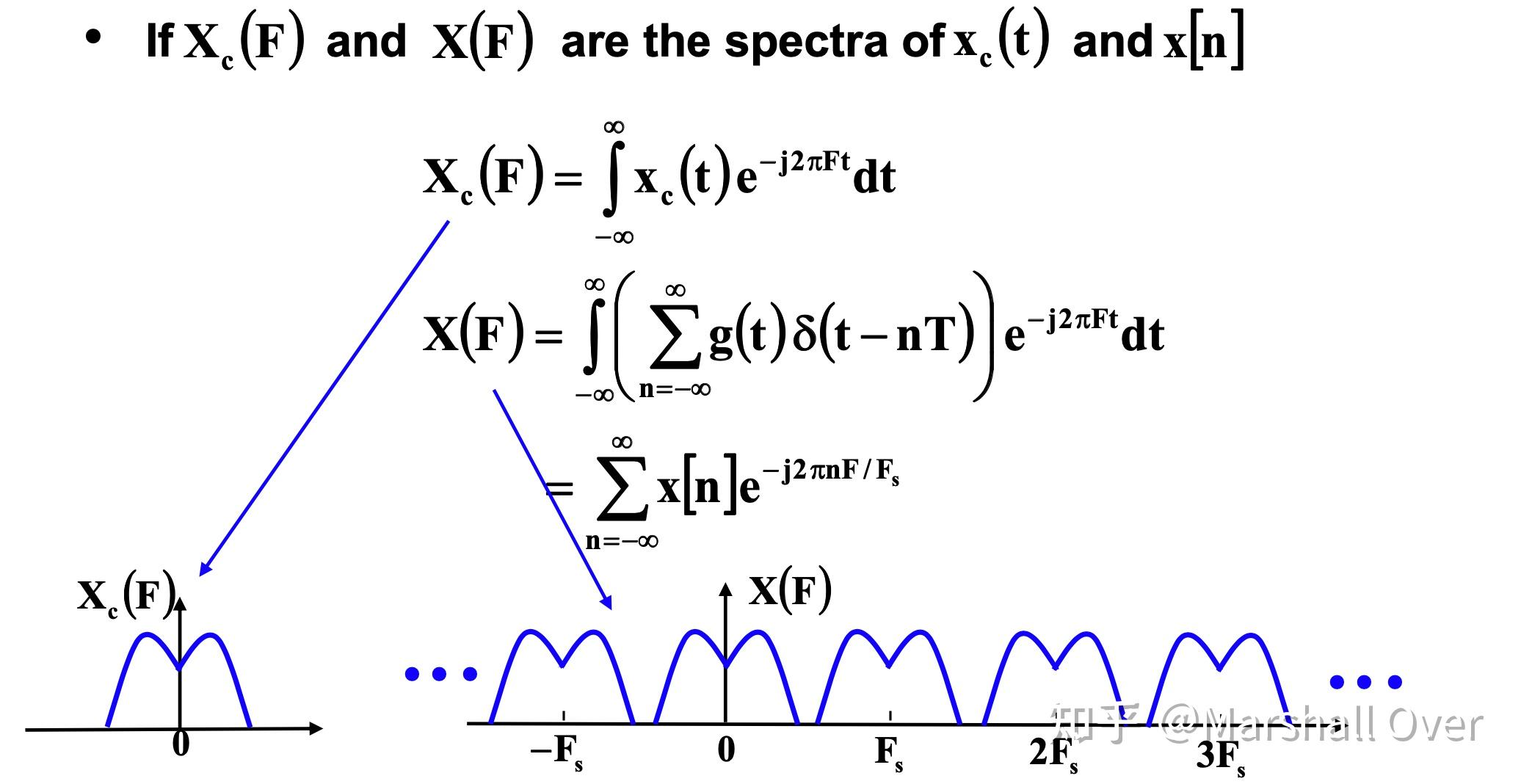
采样信号的频谱:采样周期性地复制频谱;采样信号的傅立叶变换是周期性的。
“混叠”引起的信号频谱失真:
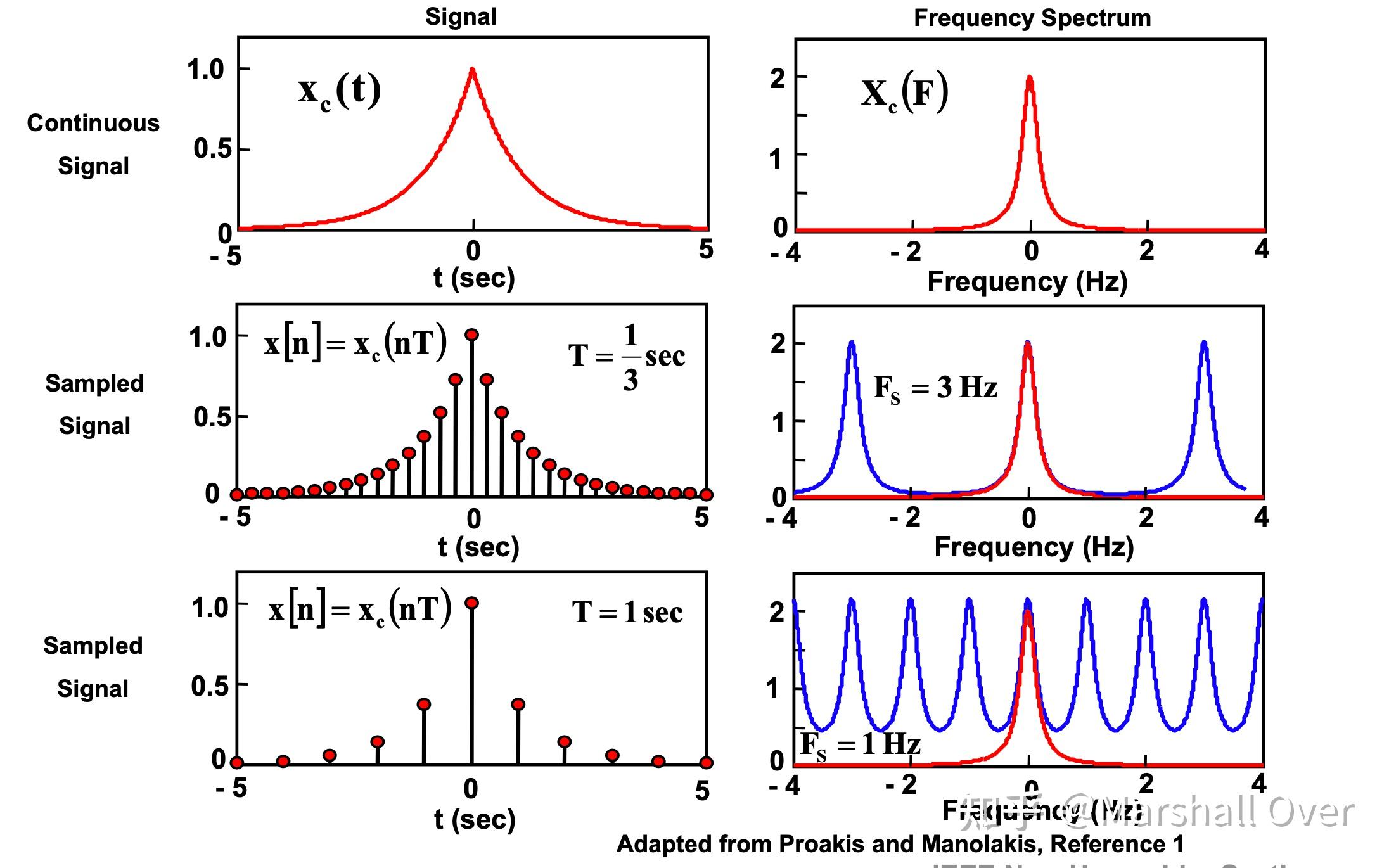
采样率对频率的影响:
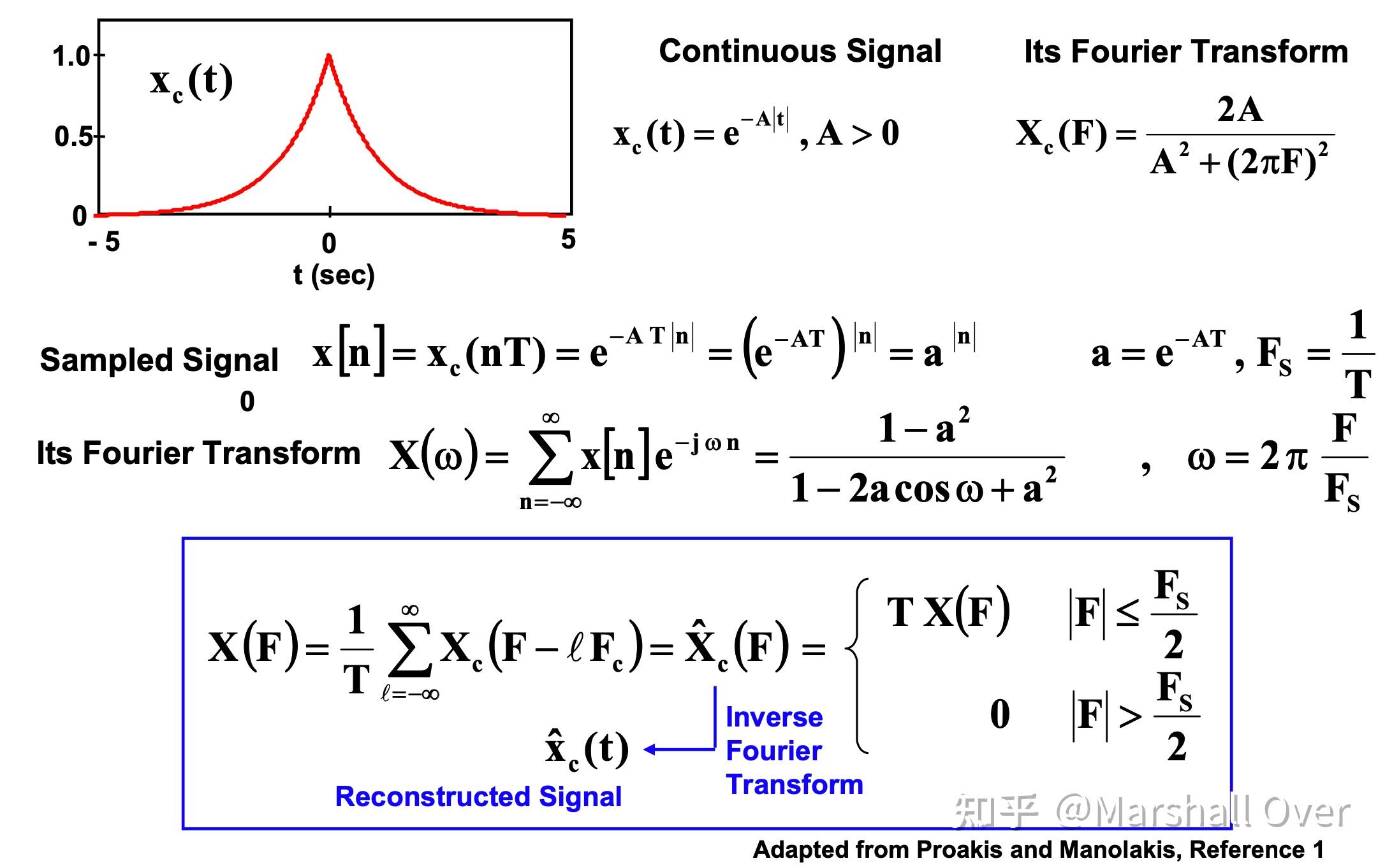
重构信号的频谱:
离散时间系统的卷积:
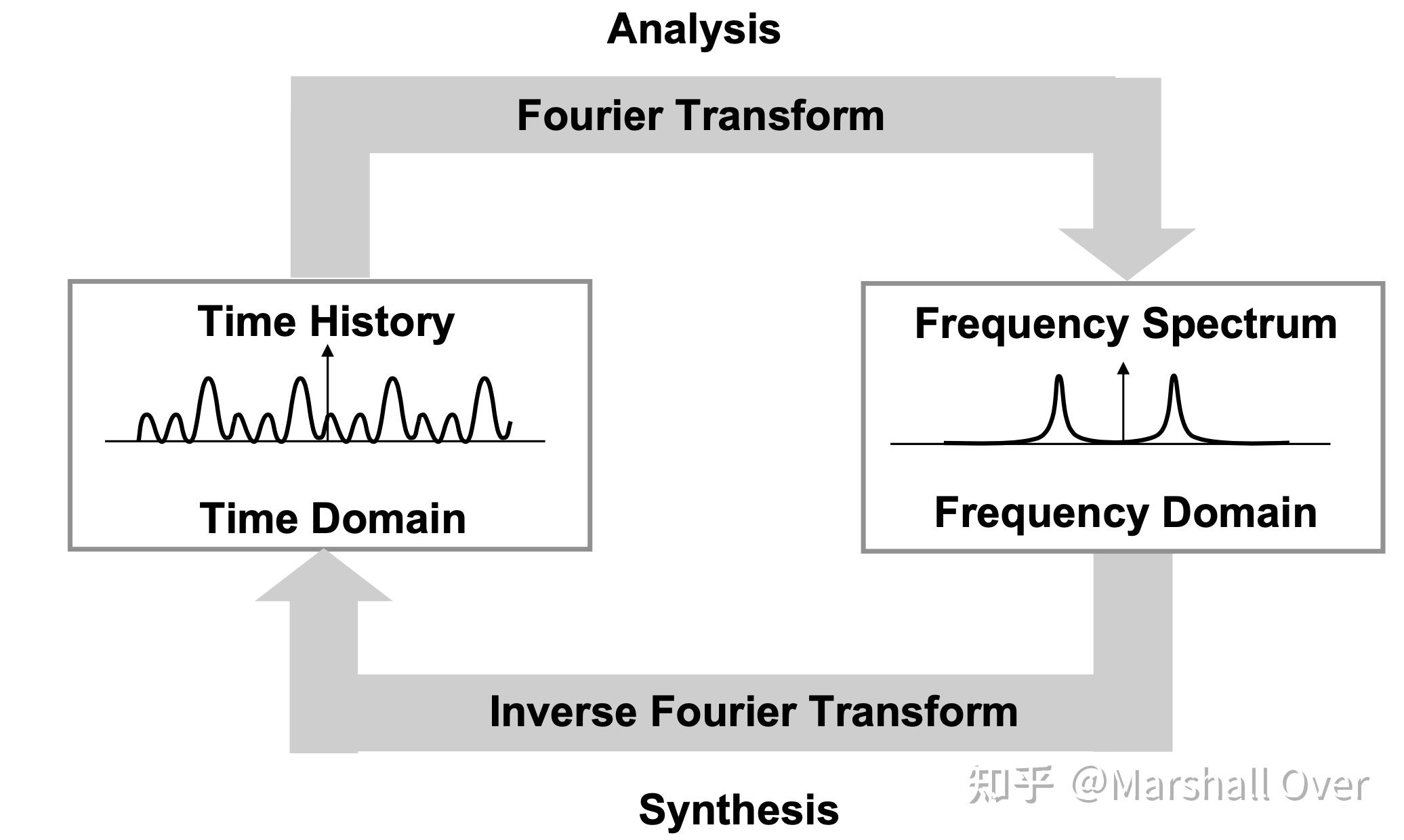
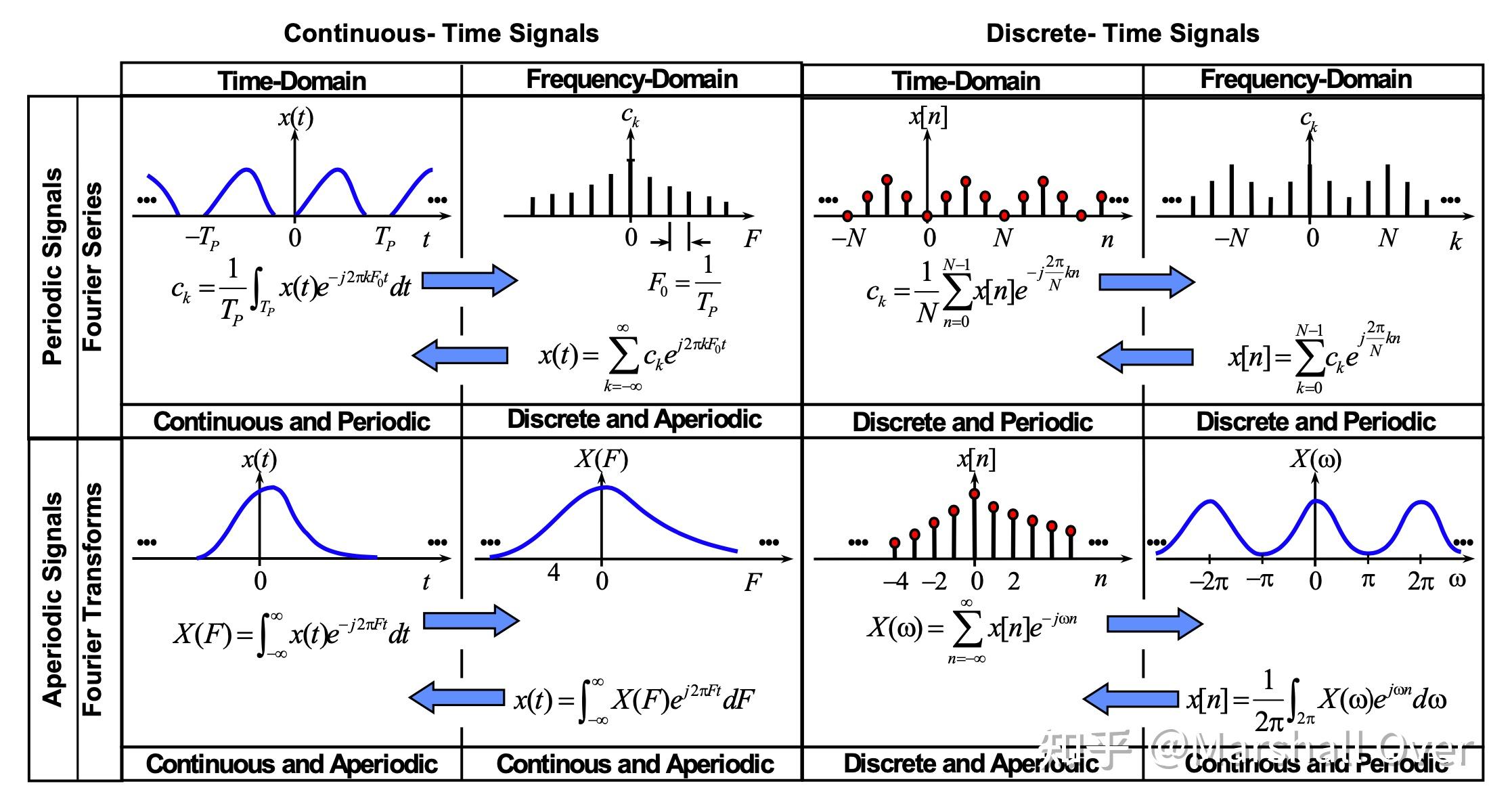
时域和频域:
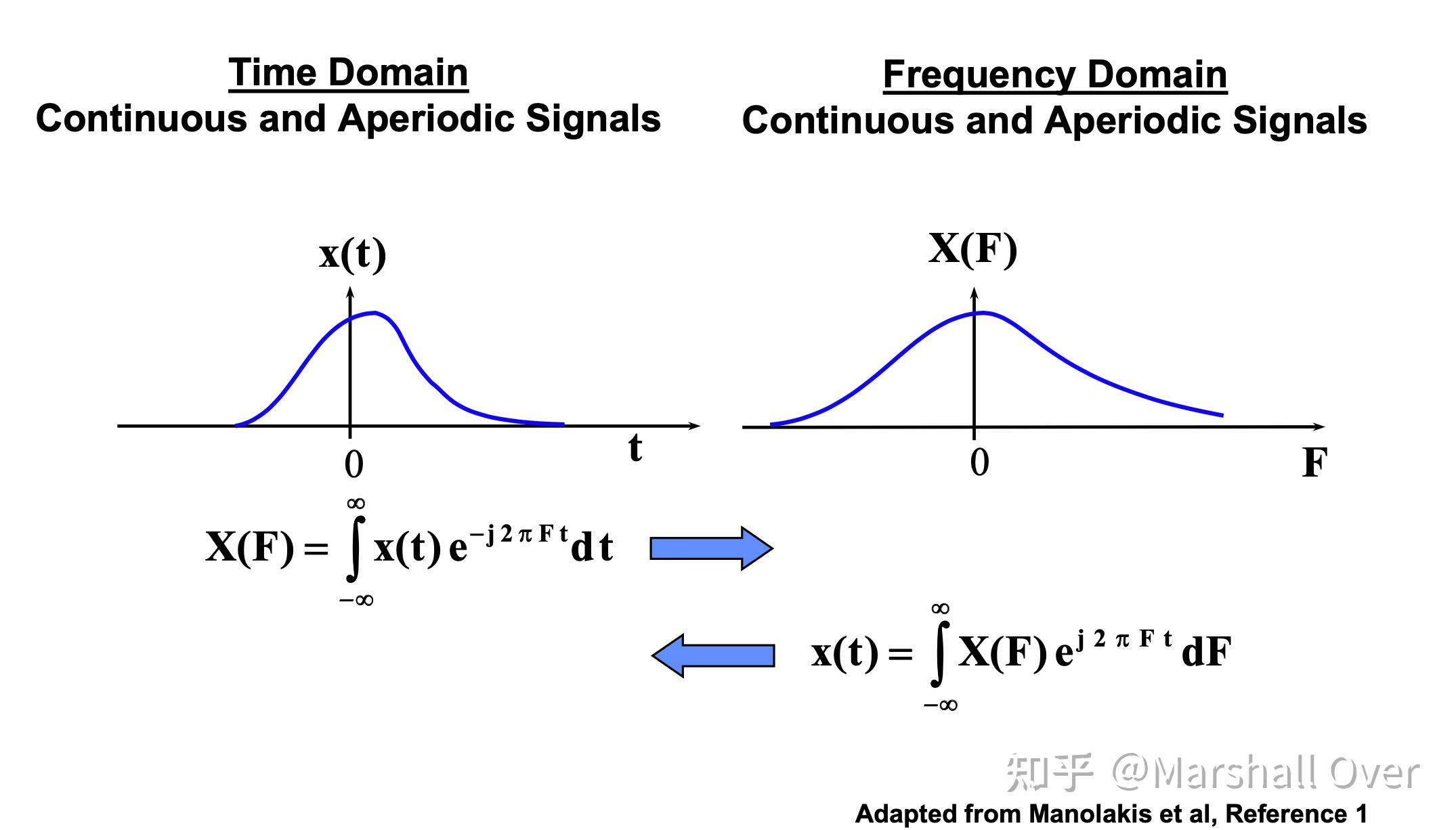
连续时间非周期信号的傅立叶变换:
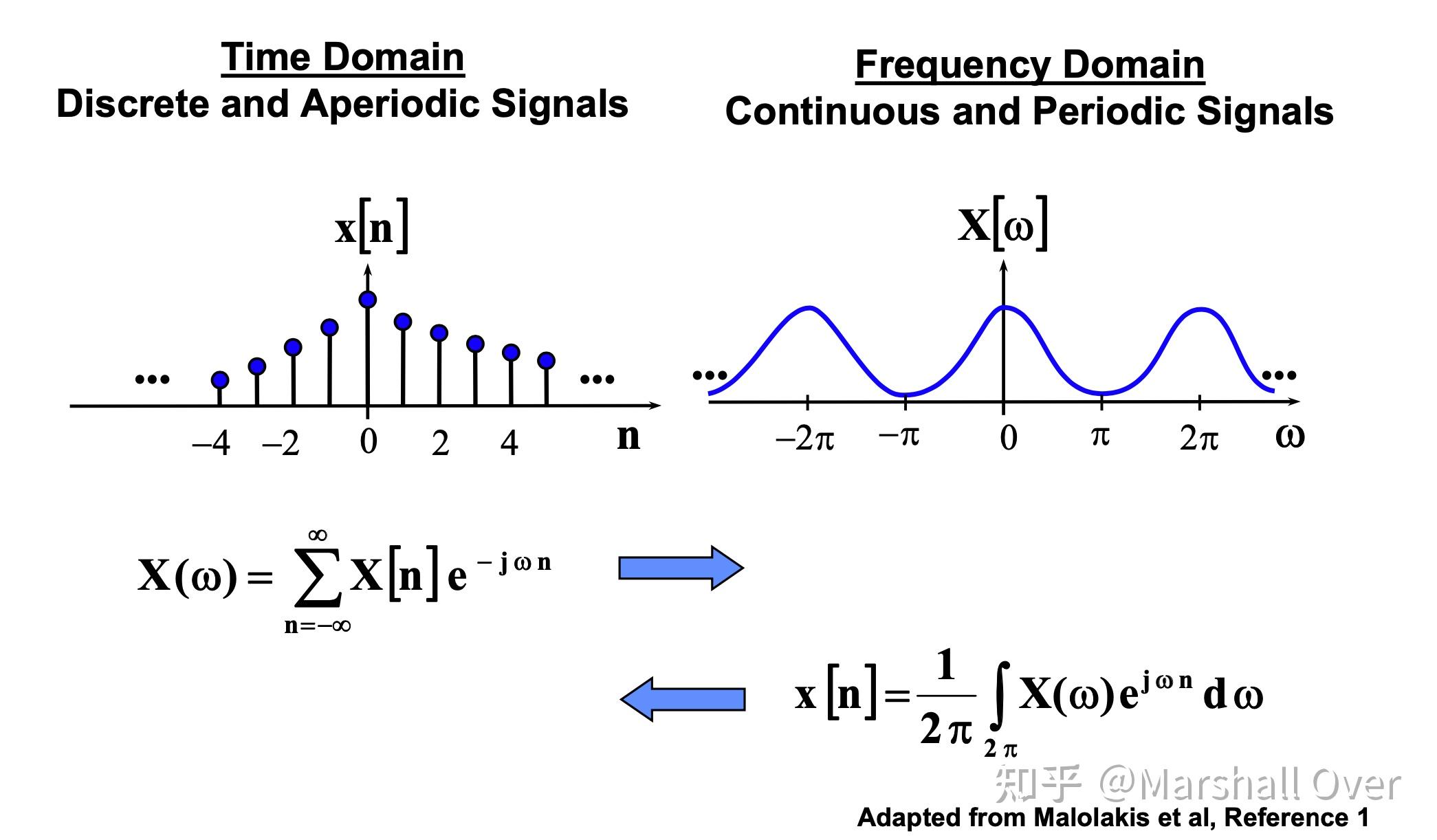
离散时间非周期信号的傅立叶变换:
时域到频域特性总结:
2.3 离散傅里叶变换
DFT:
FFT:
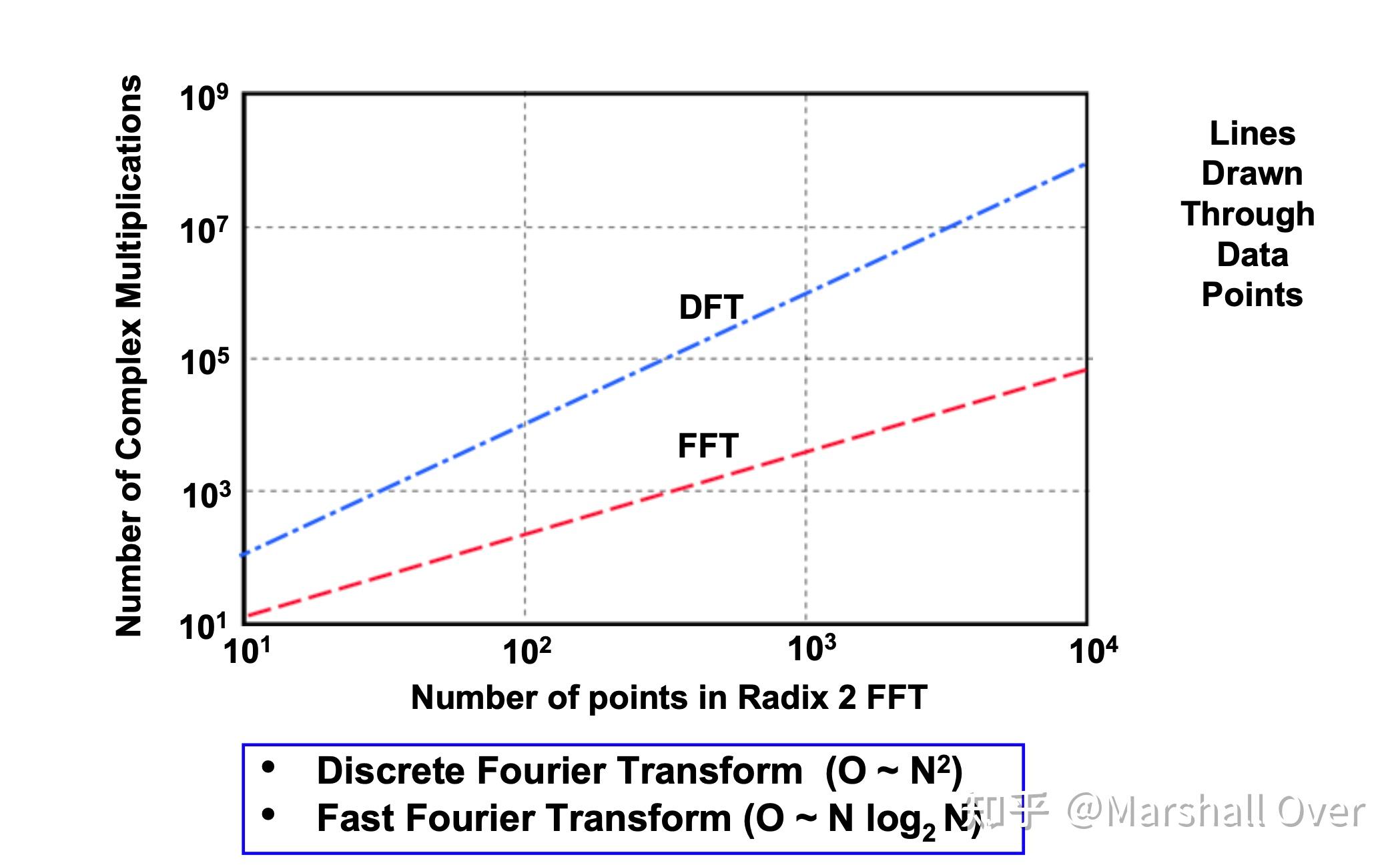
计算量对比:
FFT总结:
2.4 有限脉冲响应(FIR)滤波器
有限和无限响应滤波器:
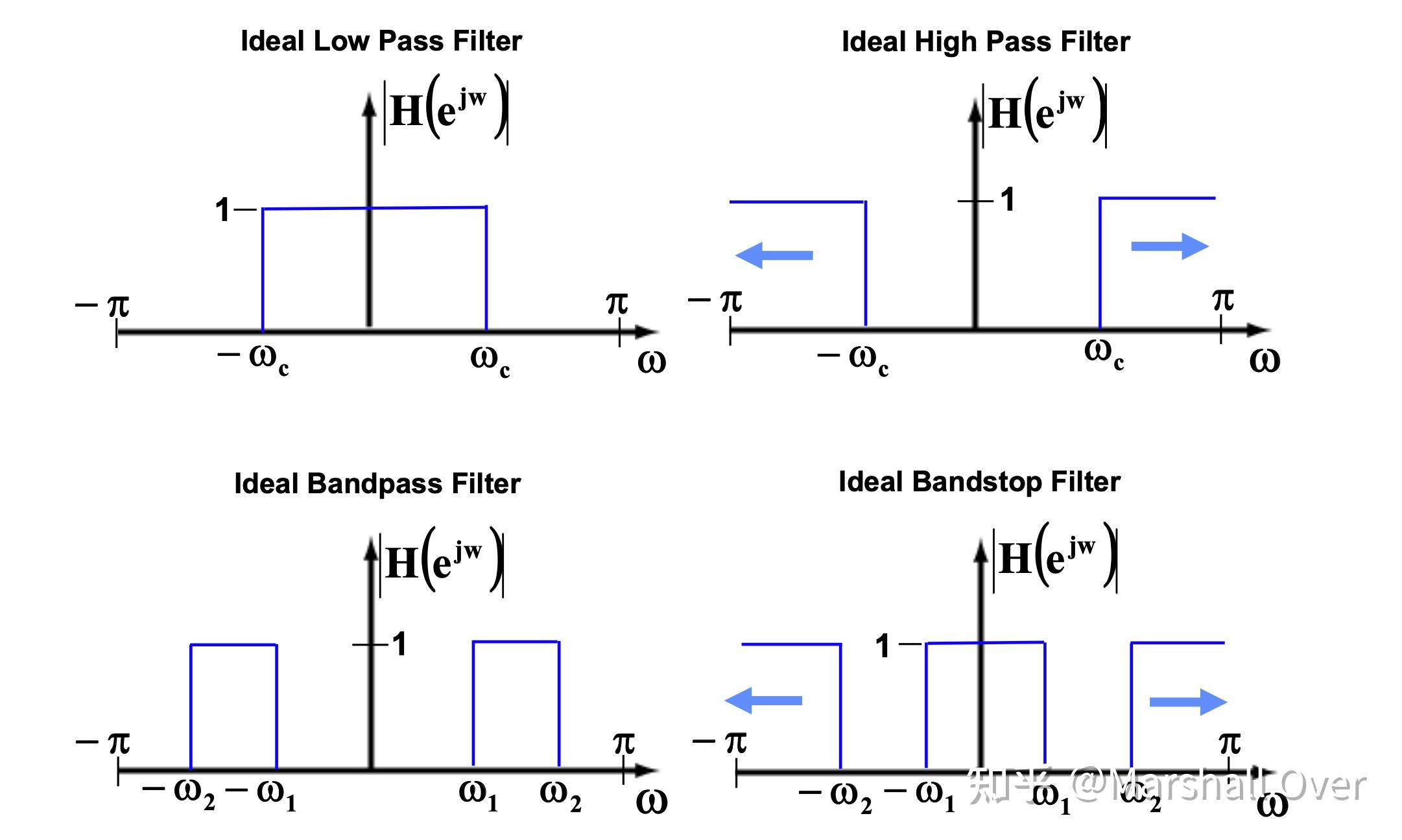
四种理想基本过滤器类型:
2.5 加权滤波器
过滤器的窗口化/加权:如果需要较低的旁瓣,以加宽通带为代价,可以将脉冲序列的元素与多个加权函数之一相乘,这将适当地调整旁瓣。
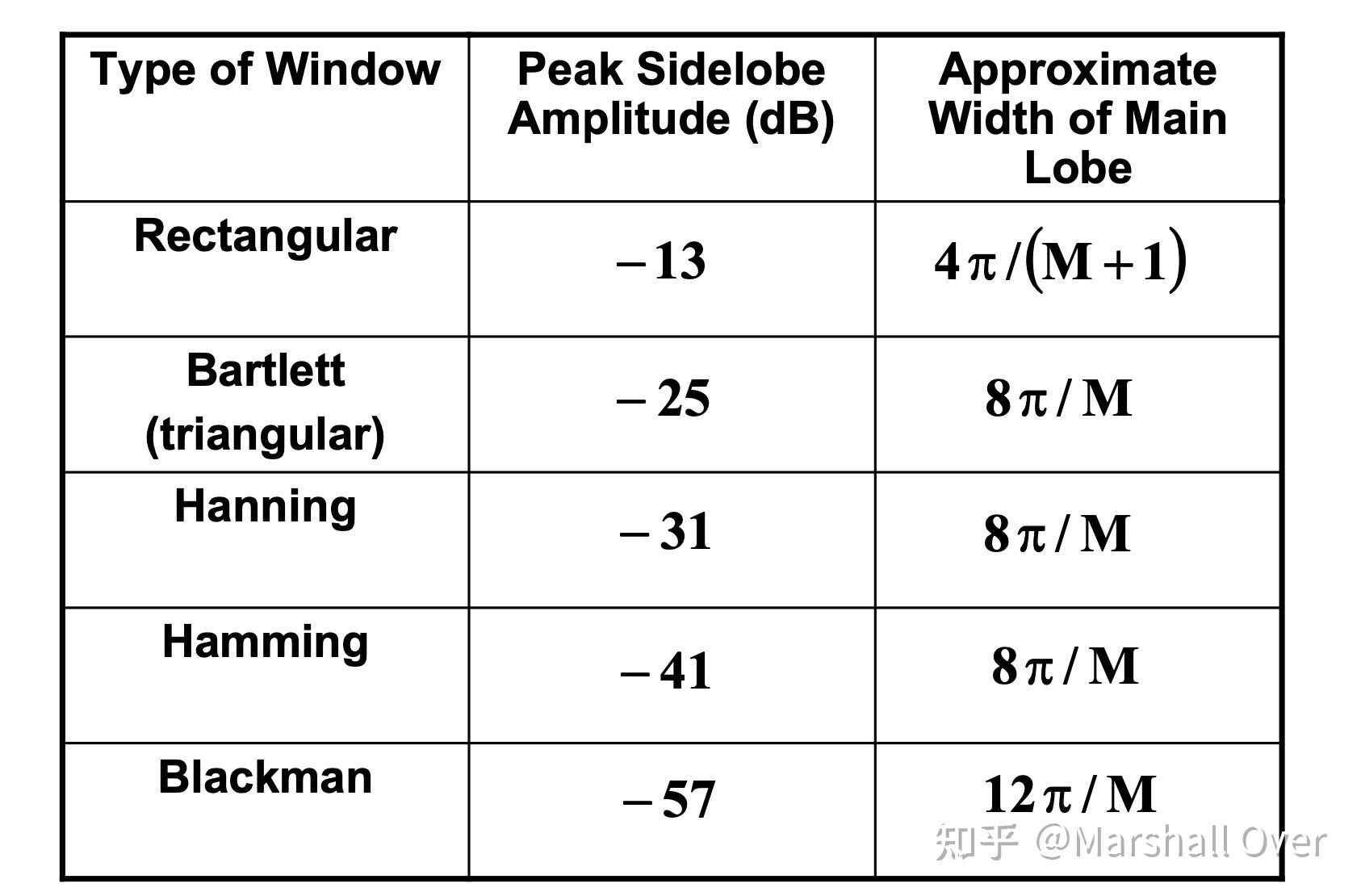
常用窗口函数:
常见窗口函数的比较:
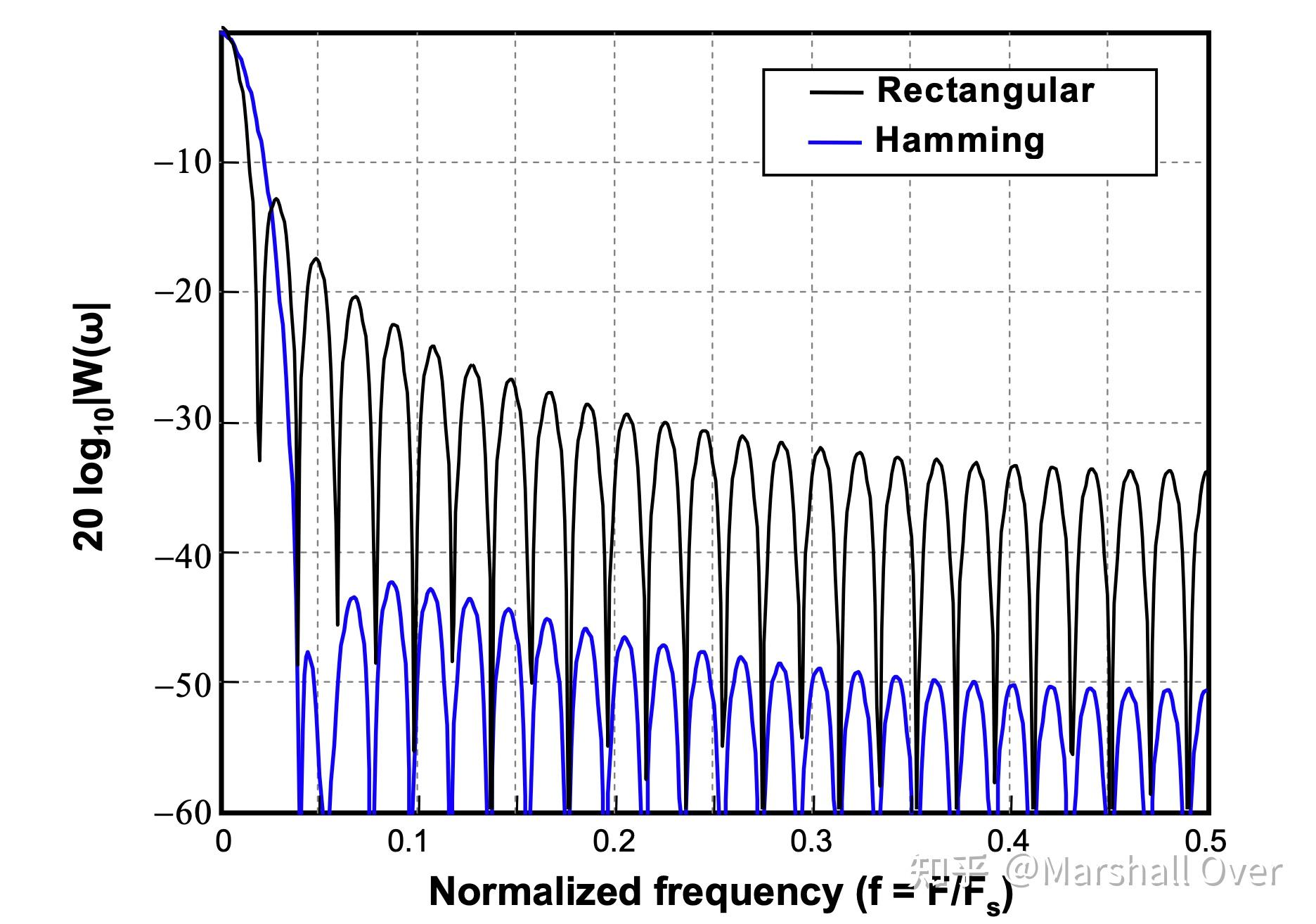
矩形窗和汉明窗的比较:
3 总结讨论
4 参考文献
[1] 百度翻译
[2] MIT 公开课: Radar Systems Engineering
[3] 维基百科

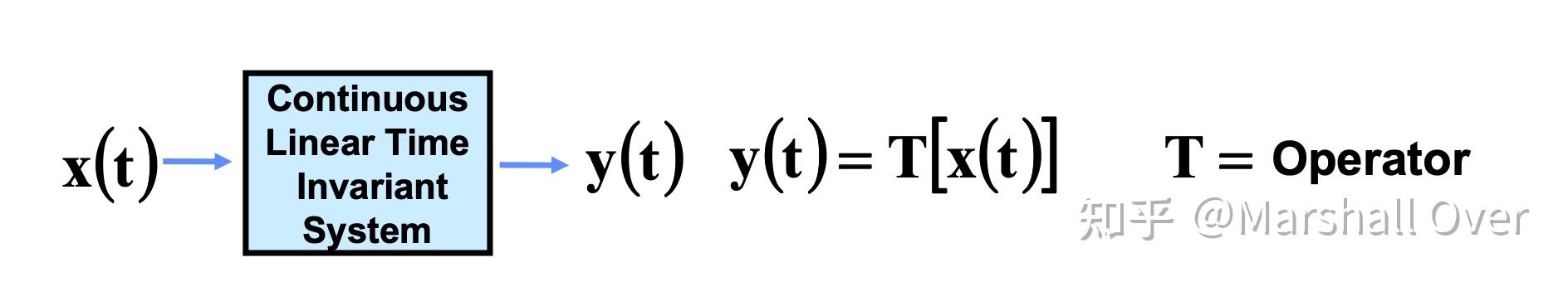













 浙公网安备 33010602011771号
浙公网安备 33010602011771号