0 写在前面
最大的幸福,就是确信有人爱你,有人因为你是你而爱你,或更确切地说,尽管你是你,有人仍然爱你。——雨果
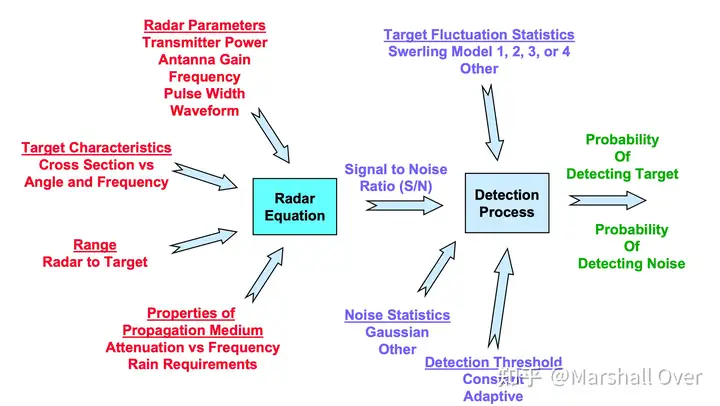
1 雷达方程简介
雷达距离方程包含:
- 目标特性:如目标反射率(雷达横截面)
- 雷达特性:如发射机功率、天线孔径
- 目标和雷达之间的距离:如距离
- 介质的特性:如大气衰减。
均匀辐射天线发射球面波的功率密度为: P_{dt} = \frac{P_t}{4\pi R^2}\tag{1} 其中P_t为发射峰值功率,R为与雷达距离。
带指向增益的辐射天线发射球面波的功率密度为: P_{dt} = \frac{P_tG_t}{4\pi R^2}\tag{2}
其中G_t为天线增益。增益是指天线在给定方向上的辐射强度高于各向同性(均匀辐射)源的辐射强度,其表达式为 G_t = \frac{4\pi A_e}{\lambda^2}\tag{3} 其中A_e为有效天线孔径面积。
雷达截面积(RCS或σ)是衡量雷达目标拦截并散射回雷达的能量的指标。目标反射信号功率为
P_r = \frac{P_tG_t}{4\pi R^2} \times \sigma \tag{4}
反射信号在雷达处的功率密度为 P_{dr} = \frac{P_tG_t}{4\pi R^2} \times \frac{\sigma}{4\pi R^2} \tag{5}
接收信号功率为雷达处的功率密度乘以接收天线的面积
P_r =\frac{P_tG_t}{4\pi R^2} \times \frac{\sigma A_e}{4\pi R^2}\tag{6}
雷达接收的噪声源主要包括:银河噪声,太阳噪声,大气噪声,地面噪声、人为干扰如雷达、无线广播等。这些噪声源的总效应由天线输出端的单个噪声源表示。接收器处的噪声功率由下式给出:
N=kB_nT_s\tag{7}
其中k=1.380649×10−23 J/K为玻尔兹曼常数,B_n为接收机噪声带宽,T_s为系统热噪声温度。
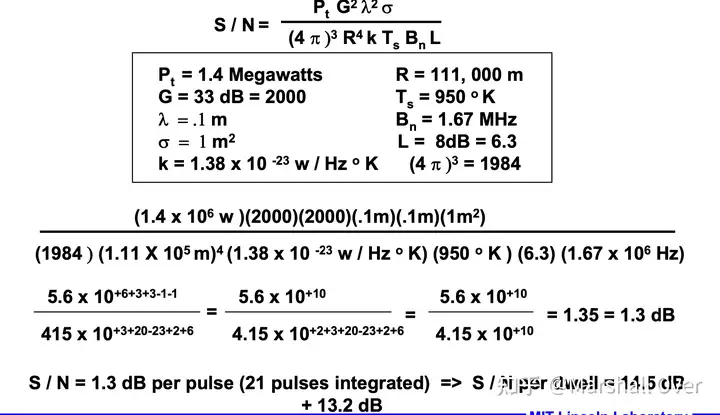
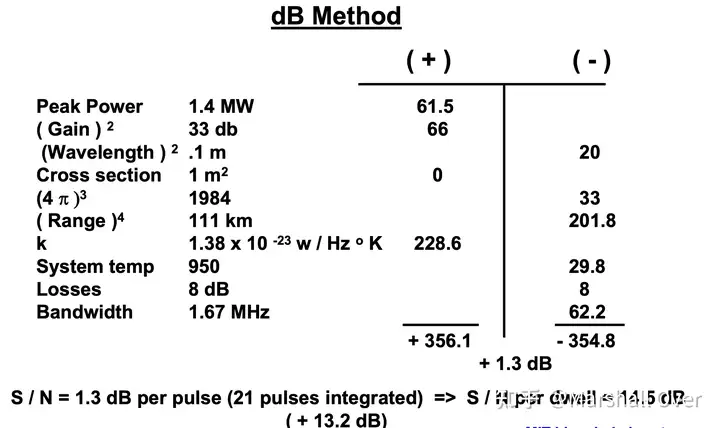
信噪比可以定以为: \frac{S}{N}=\frac{P_r}{N}=\frac{P_tG^2\lambda^2\sigma}{(4\pi)^3R^4KT_sB_nL}\tag{8}
其中L为系统损耗。信噪比(S/N或SNR)是衡量雷达在给定距离检测给定目标能力的标准指标,如在1000公里范围内的1平方米目标上,S/N=13 dB。
系统噪声温度T_s分为3个部分: T_s = T_a +T_r+L_rT_e\tag{9}
其中T_a主要来自天线,主要由天空温度和天线损耗构成;T_r主要由在天线和接收机间的射频模块产生,射频模块温度;L_r为输入射频模块损失,T_e为接收机温度。
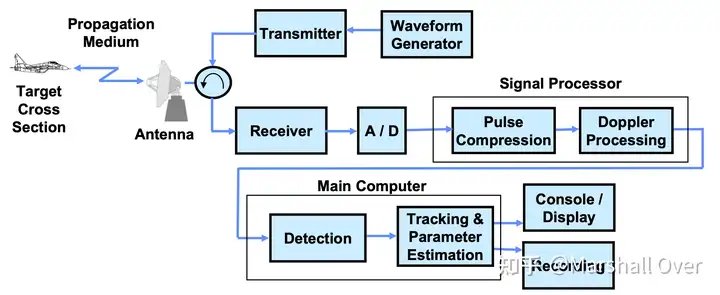
2 监视雷达方程
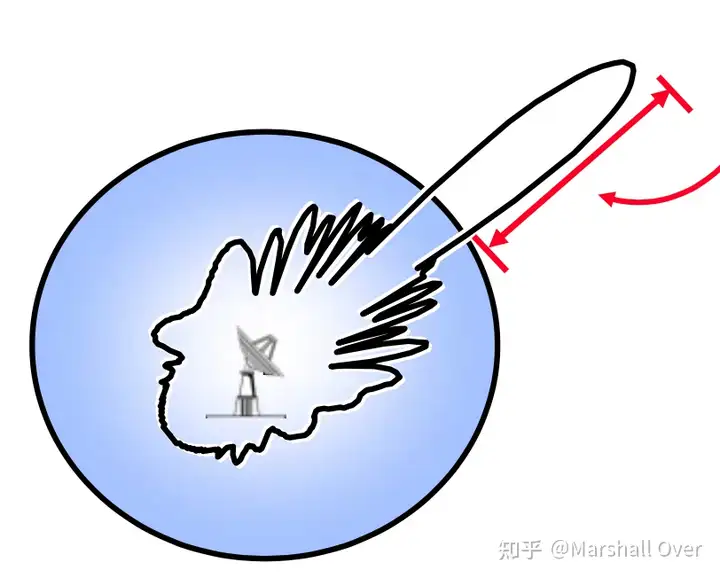
监视雷达一般具有搜素和跟踪两种状态。当目标的位置已知并且天线指向目标时,即跟踪状态下的雷达方程上节给出。当目标的位置未知时,雷达必须搜索一个大的角度区域才能找到它,搜索雷达方程如下:
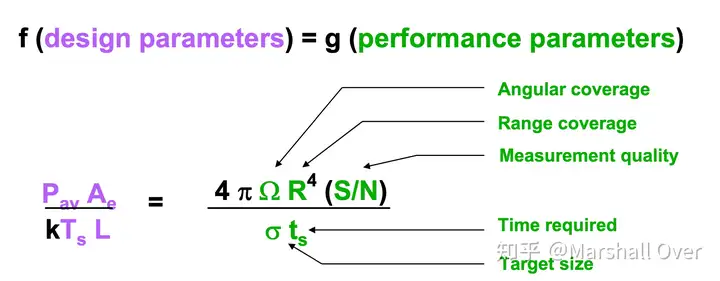
\frac{S}{N}=\frac{P_{av}A_et_s\sigma}{4\pi \Omega R^4 k T_s L}\tag{10}
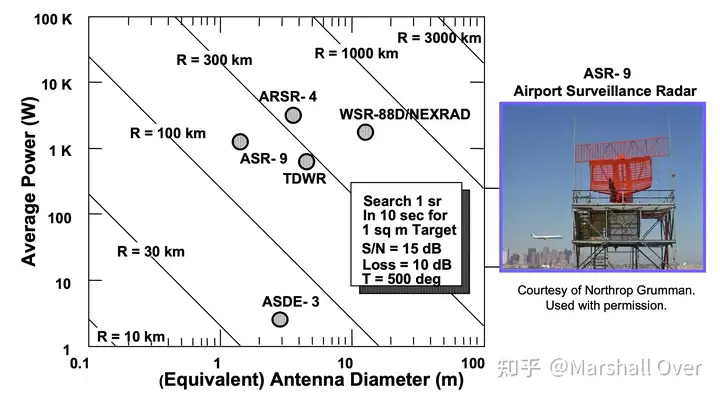
其中P_{av}雷达平均功率,\Omega为搜索空域,t_s为扫描空域所需时间。跟踪与搜索如下图所示。
搜索雷达方程可以写成如下表示形式,左边对应设计参数,右边对应性能参数。
还可以写成如下平均功率的形式
P_{av}=\frac{A_et_s\sigma(S/N)}{4\pi \Omega R^4 k T_s L}\tag{11}
可以得出,功率与波长无关,与距离成反比,是其他参数的一次函数。因此很容易进行系统修正。
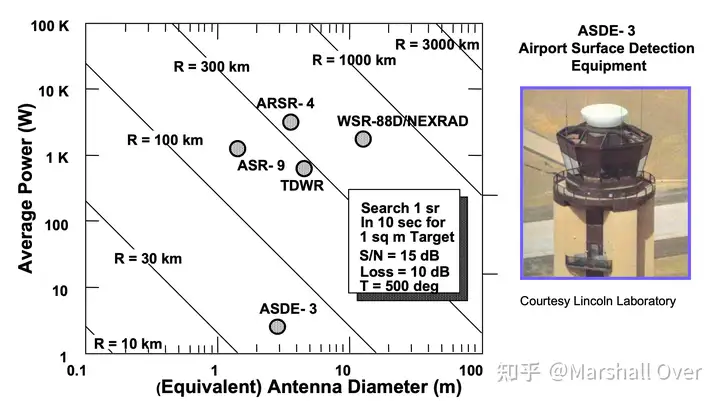
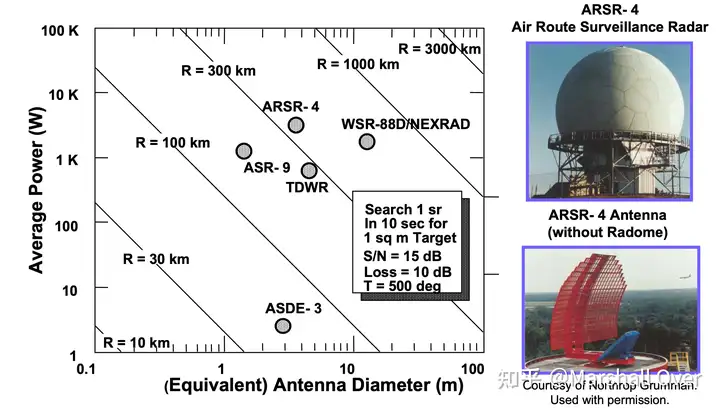
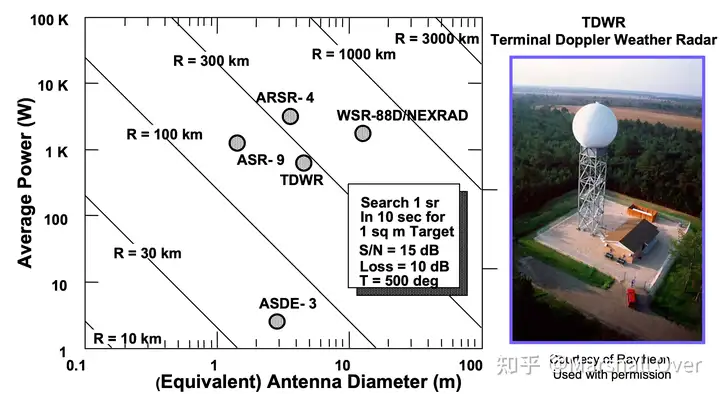
各种搜索雷达性能如下各图所示。
3 雷达损失
发射损失主要有:天线罩、波导馈电、波导、环行器、低通滤波器、旋转接头、天线效率、波束形状、扫描、量化、大气、场退化等因素构成。
接收损失主要有:天线罩、波导馈电、波导、组合器、旋转接头、接收保护器、发射/接收开关、天线效率、波束形状、扫描、量化、加权、非理想滤波器、多普勒走动、距离走动、恒虚警检测、大气、场退化等。
- 波束形状损失:使用扫描雷达从目标返回的雷达在扫描目标时会受到天线波束形状的调制。可以是2到4 dB。
- 扫描天线损失:对于相控阵天线,波束偏离瞄准线的增益小于在准线处增益。
- 管道损失:传输波导损耗,旋转接头、循环器、双工器。
- 信号处理损失:A/D量化,恒虚警损失,距离多普勒走动损失,距离多普勒加窗损失。
- 大气衰减损失:雷达波束在穿过大气层时衰减(双向损耗)。
- 积累损失:非相干积累比相干积累损失大。
- 边界/场损失:雷达的特性会随着时间的推移而恶化。传输线路中的水、接收机噪声系数恶化、发射管弱或调谐不良。
4 举个例子
5 总结讨论
雷达方程与检测过程:
- 雷达方程提供了雷达性能参数和雷达设计参数之间的简单联系;
- 对于不同的雷达功能,有不同的雷达方程;
- 雷达方程的不同形式可以让您感受到雷达设计可能会改变以适应不断变化的需求;
- 将雷达方程与成本或其他约束条件相结合,可以快速识别关键的雷达设计问题。
6 参考文献
[1] 百度翻译
[2] MIT 公开课:Introduction to Radar Systems。








 浙公网安备 33010602011771号
浙公网安备 33010602011771号