基本脉冲和连续波CW雷达操作
Github个人博客:https://joeyos.github.io
基本脉冲和连续波CW雷达操作
雷达距离方程
function [snr] = radar_eq(pt, freq, g, sigma, b, nf, loss, range)
% 代L的雷达方程
%
% Inputs:
% pt == 峰值功率 in Watts
% freq == 雷达中心频率 in Hz
% g == 天线增益 in dB
% sigma == 目标截面积 in meter squared
% b == 带宽 in Hz
% nf == 噪声系数 in dB
% loss == 雷达损耗 in dB
% range == 目标距离 in Km
%
% Outputs:
% snr == SNR in dB
%
c = 3.0e+8; % speed of light
lambda = c / freq; % wavelength
p_peak = 10*log10(pt); % convert peak power to dB
lambda_sqdb = 10*log10(lambda^2); % compute wavelength square in dB
sigmadb = 10*log10(sigma); % convert sigma to dB
four_pi_cub = 10*log10((4.0 * pi)^3); % (4pi)^3 in dB
k_db = 10*log10(1.38e-23); % Boltzman's constant in dB
to_db = 10*log10(290); % noise temp. in dB
b_db = 10*log10(b); % bandwidth in dB
range_pwr4_db = 10*log10(range.^4); % vector of target range^4 in dB
% Implement Equation (2.22)
num = p_peak + g + g + lambda_sqdb + sigmadb;
den = four_pi_cub + k_db + to_db + b_db + nf + loss + range_pwr4_db;
snr = num - den;
return
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
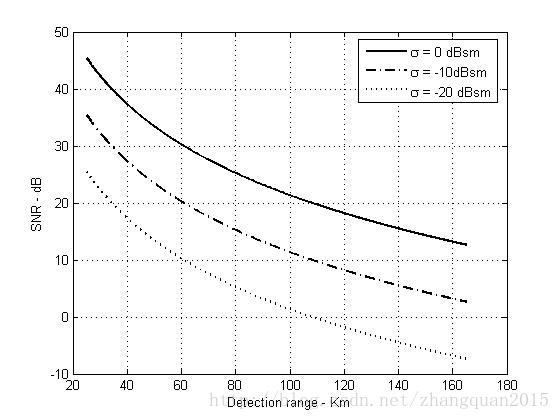
比较三种不同RCS值下的SNR随探测距离变化的曲线:
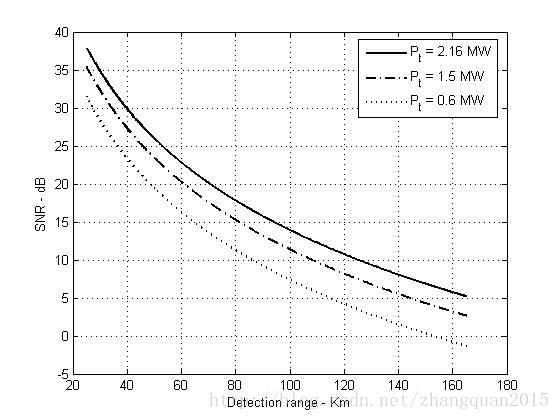
比较三种不同雷达峰值功率值情况下SNR随探测距离变化的曲线:
% Use this program to reproduce Fig. 2.1 of text.
close all
clear all
pt = 1.5e+6; % peak power in Watts
freq = 5.6e+9; % radar operating frequency in Hz
g = 45.0; % antenna gain in dB
sigma = 0.1; % radar cross section in m squared
b = 5.0e+6; % radar operating bandwidth in Hz
nf = 3.0; % noise figure in dB
loss = 6.0; % radar losses in dB
range = linspace(25e3,165e3,1000); % range to target from 25 Km 165 Km, 1000 points
snr1 = radar_eq(pt, freq, g, sigma, b, nf, loss, range);
snr2 = radar_eq(pt, freq, g, sigma/10, b, nf, loss, range);
snr3 = radar_eq(pt, freq, g, sigma*10, b, nf, loss, range);
% plot SNR versus range
figure(1)
rangekm = range ./ 1000;
plot(rangekm,snr3,'k',rangekm,snr1,'k -.',rangekm,snr2,'k:','linewidth',1.5)
grid
legend('\sigma = 0 dBsm','\sigma = -10dBsm','\sigma = -20 dBsm')
xlabel ('Detection range - Km');
ylabel ('SNR - dB');
snr1 = radar_eq(pt, freq, g, sigma, b, nf, loss, range);
snr2 = radar_eq(pt*.4, freq, g, sigma, b, nf, loss, range);
snr3 = radar_eq(pt*1.8, freq, g, sigma, b, nf, loss, range);
figure (2)
plot(rangekm,snr3,'k',rangekm,snr1,'k -.',rangekm,snr2,'k:','linewidth',1.5)
grid
legend('P_t = 2.16 MW','P_t = 1.5 MW','P_t = 0.6 MW')
xlabel ('Detection range - Km');
ylabel ('SNR - dB');
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
低PRF雷达方程
function [snr] = lprf_req(pt, g, freq, sigma, np, b, nf, loss, range)
% This program implements Eq. (2.27) of textbook
%
% Inputs:
% pt == 峰值功率 in Watts
% freq == 雷达中心频率 in Hz
% g == 天线增益 in dB
% sigma == 目标截面积 in meter squared
% b == 带宽 in Hz
% nf == 噪声系数 in dB
% np == 脉冲个数
% loss == 雷达损耗 in dB
% range == 目标距离(单值或者向量) in Km
%
% Outputs:
% snr == SNR in dB
%
c = 3.0e+8; % speed of light
lambda = c / freq; % wavelength
p_peak = 10*log10(pt); % convert peak power to dB
lambda_sqdb = 10*log10(lambda^2); % compute wavelength square in dB
sigmadb = 10*log10(sigma); % convert sigma to dB
four_pi_cub = 10*log10((4.0 * pi)^3); % (4pi)^3 in dB
k_db = 10*log10(1.38e-23); % Boltzman's constant in dB
to_db = 10*log10(290); % noise temp. in dB
b_db = 10*log10(b); % bandwidth in dB
np_db = 10.*log10(np); % number of pulses in dB
range_pwr4_db = 10*log10(range.^4); % vector of target range^4 in dB
% Implement Equation (1.68)
num = p_peak + g + g + lambda_sqdb + sigmadb + np_db;
den = four_pi_cub + k_db + to_db + b_db + nf + loss + range_pwr4_db;
snr = num - den;
return
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
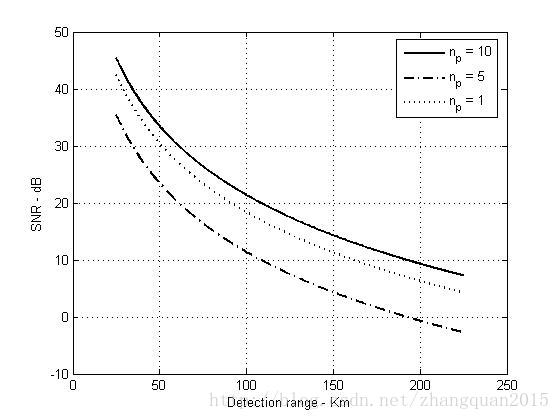
探测距离与脉冲个数与SNR的关系:
% Use this program to reproduce Fig. 2.2 of text.
close all
clear all
pt = 1.5e+6; % peak power in Watts
freq = 5.6e+9; % radar operating frequency in Hz
g = 45.0; % antenna gain in dB
sigma = 0.1; % radar cross section in m squared
b = 5.0e+6; % radar operating bandwidth in Hz
nf = 3.0; %noise figure in dB
loss = 6.0; % radar losses in dB
np = 1;
range = linspace(25e3,225e3,1000); % range to target from 5 Km 225 Km, 1000 points
snr1 = lprf_req(pt, g, freq, sigma, np, b, nf, loss, range);
snr2 = lprf_req(pt, g, freq, sigma, 5*np, b, nf, loss, range);
snr3 = lprf_req(pt, g, freq, sigma, 10*np, b, nf, loss, range);
% plot SNR versus range
figure(1)
rangekm = range ./ 1000;
plot(rangekm,snr3,'k',rangekm,snr1,'k -.',rangekm,snr2,'k:','linewidth',1.5)
grid
legend('n_p = 10','n_p = 5','n_p = 1')
xlabel ('Detection range - Km');
ylabel ('SNR - dB');
np = linspace(1,500,500);
range = 150e3;
snr1 = lprf_req(pt, g, freq, sigma, np, b, nf, loss, range);
snr2 = lprf_req(pt, g, freq, 10*sigma, np, b, nf, loss, range);
figure (2)
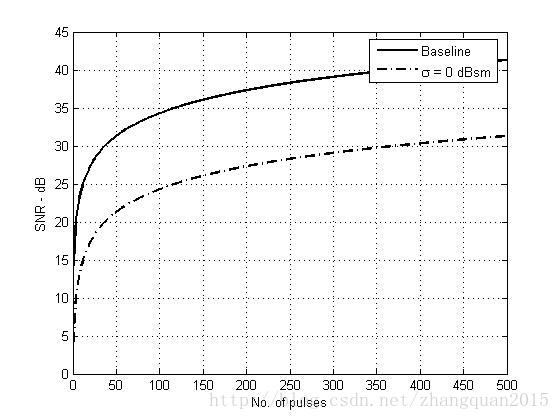
plot(np,snr2,'k',np,snr1,'k -.','linewidth',1.5)
grid
legend('Baseline','\sigma = 0 dBsm')
xlabel ('No. of pulses');
ylabel ('SNR - dB');
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
高PRF雷达方程
function [snr] = hprf_req (pt, Ti, g, freq, sigma, dt, range, nf, loss)
% This program implements Eq. (2.31)of textbook
%
% Inputs:
% pt == 峰值功率 in Watts
% freq == 中心频率 in Hz
% g == 天线增益 in dB
% sigma == 目标截面积 in meter squared
% Ti == 目标上的时间 in seconds
% nf == 噪声系数 in dB
% dt == 占空因子
% loss == 雷达损耗 in dB
% range == 目标距离(单值或者向量) in Km
%
% Outputs:
% snr == SNR in dB
%
c = 3.0e+8; % speed of light
lambda = c / freq; % wavelength
pav = 10*log10(pt*dt); % compute average power in dB
Ti_db = 10*log10(Ti); % time on target in dB
lambda_sqdb = 10*log10(lambda^2); % compute wavelength square in dB
sigmadb = 10*log10(sigma); % convert sigma to dB
four_pi_cub = 10*log10((4.0 * pi)^3); % (4pi)^3 in dB
k_db = 10*log10(1.38e-23); % Boltzman's constant in dB
to_db = 10*log10(290); % noise temp. in dB
range_pwr4_db = 10*log10(range.^4); % vector of target range^4 in dB
% Implement Equation (1.72)
num = pav + Ti_db + g + g + lambda_sqdb + sigmadb;
den = four_pi_cub + k_db + to_db + nf + loss + range_pwr4_db;
snr = num - den;
return
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
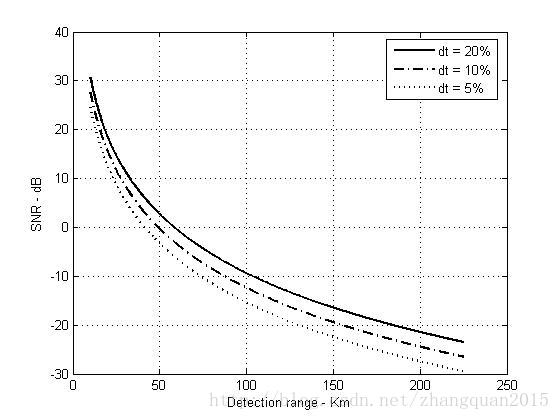
占空因子和探测距离与SNR的关系:
% Use this program to reproduce Fig. 2.3 of text.
close all
clear all
pt = 10e03; % peak power in Watts
freq = 5.6e+9; % radar operating frequency in Hz
g = 20; % antenna gain in dB
sigma = 0.01; % radar cross section in m squared
b = 5.0e+6; % radar operating bandwidth in Hz
nf = 3.0; %noise figure in dB
loss = 8.0; % radar losses in dB
Ti = 2; % time on target in seconds
dt = .05; % 5% duty cycle
range = linspace(10e3,225e3,1000); % range to target from 10 Km 225 Km, 1000 points
snr1 = hprf_req (pt, Ti, g, freq, sigma, .05, range, nf, loss);
snr2 = hprf_req (pt, Ti, g, freq, sigma, .1, range, nf, loss);
snr3 = hprf_req (pt, Ti, g, freq, sigma, .2, range, nf, loss);
% plot SNR versus range
figure(1)
rangekm = range ./ 1000;
plot(rangekm,snr3,'k',rangekm,snr2,'k -.',rangekm,snr1,'k:','linewidth',1.5)
grid
legend('dt = 20%','dt = 10%','dt = 5%')
xlabel ('Detection range - Km');
ylabel ('SNR - dB');
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
监视雷达方程
某个特定的雷达系统必须完成的首要任务是连续扫描空间的特定区域来搜索感兴趣的目标。一旦探测建立,由雷达信号和数据处理机提取出诸如距离、角度位置,可能还有目标速度等目标信息。究竟采取何种搜索模式,取决于雷达的设计和天线。
function PAP = power_aperture(snr,tsc,sigma,range,nf,loss,az_angle,el_angle)
% This function implements Eq. (2.38) of textbook
%
% Inputs:
% snr == 灵敏度 in dB
% tsc == 扫描时间 in seconds
% sigma == 目标截面积 in meter squared
% range == 目标距离 in Km
% nf == 噪声系数 in dB
% loss == 雷达损耗 in dB
% az_angle == 搜索区域方位上的范围 in degrees
% el_angle == 搜索区域仰角上的范围 in degrees
%
% Outputs:
% PAP == 功率孔径积 in dB
%
Tsc = 10*log10(tsc); % convert Tsc into dB
Sigma = 10*log10(sigma); % convert sigma to dB
four_pi = 10*log10(4.0 * pi); % (4pi) in dB
k_db = 10*log10(1.38e-23); % Boltzman's constant in dB
To = 10*log10(290); % noise temp. in dB
range_pwr4_db = 10*log10(range.^4); % target range^4 in dB
omega = (az_angle/57.296) * (el_angle / 57.296); % compute search volume in steraradians
Omega = 10*log10(omega); % search volume in dB
% implement Eq. (1.79)
PAP = snr + four_pi + k_db + To + nf + loss + range_pwr4_db + Omega ...
- Sigma - Tsc;
return
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
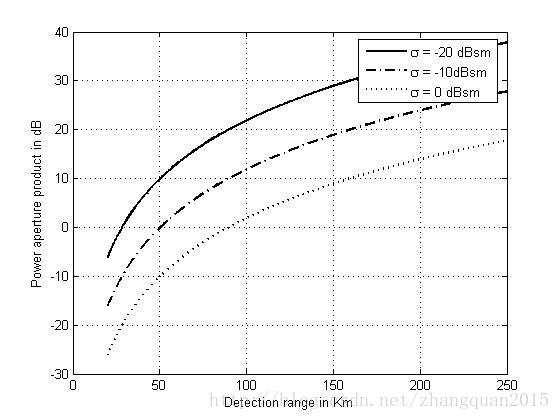
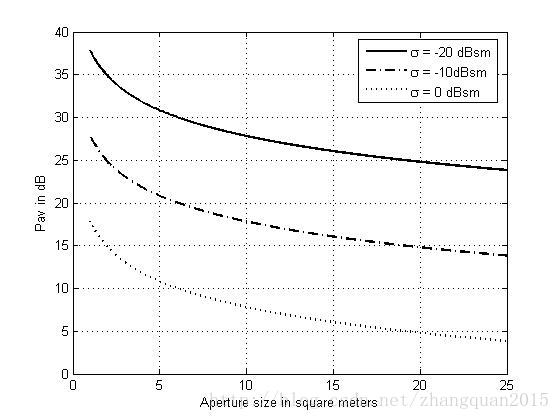
给出三种RCS选择的功率孔径积和探测距离的关系曲线,以及雷达平均功率与功率孔径积的关系曲线图:
% Use this program to reproduce Fig. 2.6 of text.
close all
clear all
tsc = 2.5; % Scan time i s2.5 seconds
sigma = 0.1; % radar cross section in m squared
te = 900.0; % effective noise temperature in Kelvins
snr = 15; % desired SNR in dB
nf = 6.0; %noise figure in dB
loss = 7.0; % radar losses in dB
az_angle = 2; % search volume azimuth extent in degrees
el_angle = 2; %serach volume elevation extent in degrees
range = linspace(20e3,250e3,1000); % range to target from 20 Km 250 Km, 1000 points
pap1 = power_aperture(snr,tsc,sigma/10,range,nf,loss,az_angle,el_angle);
pap2 = power_aperture(snr,tsc,sigma,range,nf,loss,az_angle,el_angle);
pap3 = power_aperture(snr,tsc,sigma*10,range,nf,loss,az_angle,el_angle);
% plot power aperture prodcut versus range
% generate Figure 2.6a
figure(1)
rangekm = range ./ 1000;
plot(rangekm,pap1,'k',rangekm,pap2,'k -.',rangekm,pap3,'k:','linewidth',1.5)
grid
legend('\sigma = -20 dBsm','\sigma = -10dBsm','\sigma = 0 dBsm')
xlabel ('Detection range in Km');
ylabel ('Power aperture product in dB');
% generate Figure 2.6b
lambda = 0.03; % wavelength in meters
G = 45; % antenna gain in dB
ae = linspace(1,25,1000);% aperture size 1 to 25 meter squared, 1000 points
Ae = 10*log10(ae);
range = 250e3; % rnage of interset is 250 Km
pap1 = power_aperture(snr,tsc,sigma/10,range,nf,loss,az_angle,el_angle);
pap2 = power_aperture(snr,tsc,sigma,range,nf,loss,az_angle,el_angle);
pap3 = power_aperture(snr,tsc,sigma*10,range,nf,loss,az_angle,el_angle);
Pav1 = pap1 - Ae;
Pav2 = pap2 - Ae;
Pav3 = pap3 - Ae;
figure(2)
plot(ae,Pav1,'k',ae,Pav2,'k -.',ae,Pav3,'k:','linewidth',1.5)
grid
xlabel('Aperture size in square meters')
ylabel('Pav in dB')
legend('\sigma = -20 dBsm','\sigma = -10dBsm','\sigma = 0 dBsm')
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
带干扰的雷达方程
任何有意干扰雷达正常工作的电子措施通常称为电子对抗ECM。其中包括箔条、雷达诱饵、雷达RCS变更。
自屏蔽干扰器SSJ
烧穿距离
远距离干扰器SOJ
距离缩减因子
双基地雷达方程
雷达损耗
发射和接收损耗
发射和接收损耗分别发生在雷达发射机和天线输入端口之间及天线输出端口和接收机前端之间,这样的损耗统称为管道损耗。典型的管道损耗是1-2dB。
天线方向图损耗和扫描损耗
在使用雷达方程时,我们都假设了天线的最大增益,这仅仅在目标位于沿天线视线轴的方向时成立。
大气损耗
大气衰减是雷达工作频率、目标距离和仰角的函数,大气衰减可以高到几个dB。
折叠损耗
积累的返回噪声脉冲数量大于从目标返回的脉冲数,称为折叠损耗。
处理损耗
- 检波的近似
- 恒虚警率损耗
- 量化损耗
- 距离门跨越
- 多普勒滤波器跨越
- 其他




 浙公网安备 33010602011771号
浙公网安备 33010602011771号