【P8593】一个弹的投

前言

感觉属于信竞和物理的缝合，怕不是学长被物理虐的太惨了的报复？

比赛时间撞了校内模拟赛，然后这场没打，不然至少能过这题。

正文

题意有点晕乎，大概就是说，有 \(n\) 个导弹，各自从 \((x_i,y_i)\) 开始平抛运动，当两个导弹撞一起时，杀伤力加大一个。

然后有防御措施，问怎样防护最优，输出受到最小杀伤力。

题目给了个平抛落点公式，但实际上没有太大用处：

\[x_t=x_i+v_i\sqrt{\dfrac{2y_i}g} \]

首先考虑两个导弹咋撞上，这里需要一点物理知识（

平抛运动的运动轨迹可以理解为是物体本身的速度 \(v_i\) 和自由落体的速度的合速度，显然发现每个导弹他们每时每刻自由落体的速度啥啥都一样（除非落地）。

也就是说，\(y_i\) 本来就不等的，除非掉到 \(x\) 轴，都不会相等；\(y_i\) 本来就相等的，一直都会相等。

剩下就要考虑 \(x_i\)。

我们来整个图看看：

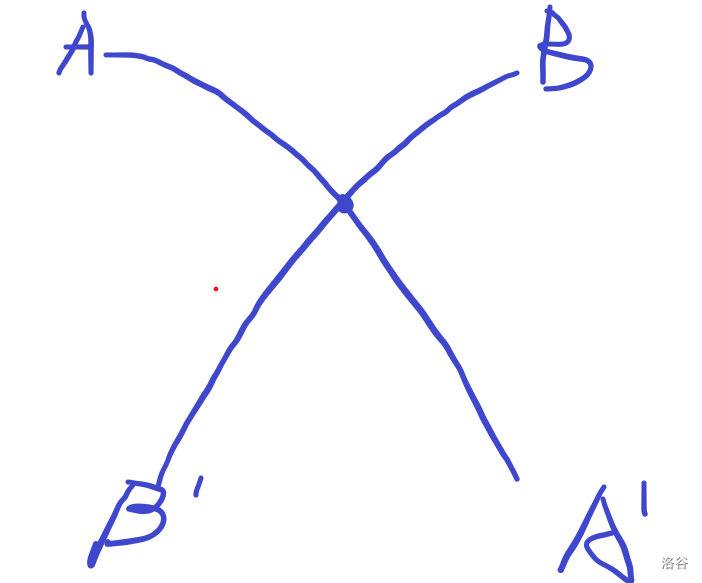
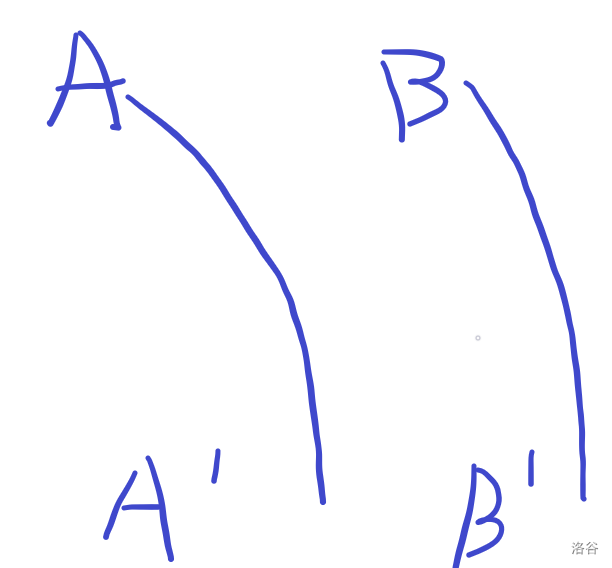
容易发现，如果落地后两点的先后顺序改变，则必定产生一个交点。

如何计算呢？逆序对。

将 \(y_i\) 相同的按 \(x_i\) 排序，记录编号，再求出落点 \(u_i\)，排序（那个公式就在这用一下），最后直接算逆序对即可。