【文文殿下】Manache算法-学习笔记
Manache算法
定义:是一个判断回文子串的算法,我们结合例题解释:
题目:给定一个长度为 n 的字符串 S,求其最长回文子串 一个字符串是回文的,当且仅当反转后的串与原串完全相等
分析:对于这个题目,有三种主流思路:
一:Hash+二分
计算字符串的前缀hash值
枚举中点,二分回文字串的长度
时间复杂度:$O(nlogn)$
二:回文自动机
复杂度是线性的,但是编程复杂度极高,思维难度极高。
三:Manache算法
复杂度是线性的,思维难度低,编程难度低
讲解Manache方法
对于Manache算法,我们先考虑朴素做法:枚举回文串中心,然后向两边扩展,这样的复杂度是$O(N^2)$的,
但是类比KMP算法,我们在朴素算法中,没有考虑到已经计算的部分对于之后结果的贡献,朴素方法的突破口就在这里了。
考虑优化:由于回文串长度分奇偶,有点麻烦,所以,我们考虑在每个字符中间插入一个'#'字符,来保证字符串的奇性。特别的,在字符串前两个字符,插入\$和#,对于\$的作用是:防止数组越界,既下文代码中的whie()函数,来确保其遇到字符串开头立即停止(因为对于$字符,其为唯一的,不可能有字符与其匹配)。
我们引入辅助数组$len[i]$ 来表示以$i$为中心,最大回文串的半径,显然的,对于每一个$len[i]$,$len[i]-1$就是原来回文串的长度,我们结合一个样例来说明:
原字符串:$ # A # B # A # A # B #
$len$数组 1 1 2 1 4 1 2 2 2 1 2 1
原来的最长回文串是$3$ 也就是$len[4]-1$ (从0开始标号)。
对吧?
接下来的问题,就是如何计算$len$数组了 , 这确实是个问题,不过我们可以通过下面的办法解决:
考虑$len[i]$ 以及当前求出的回文右边界$mx$ , $id$ 是对应的回文中心,如果$i<mx$ 则附上初值$min{mx-i,p[j]}$,其中,$j$是$i$关于$id$的对称坐标,通过中点坐标公式,我们可以得出:$j=id*2-i$ 。
否则($i>=mx$)附上初值$len[i]=1$.
然后,向两边扩展就好了。可以结合下面的图像理解:
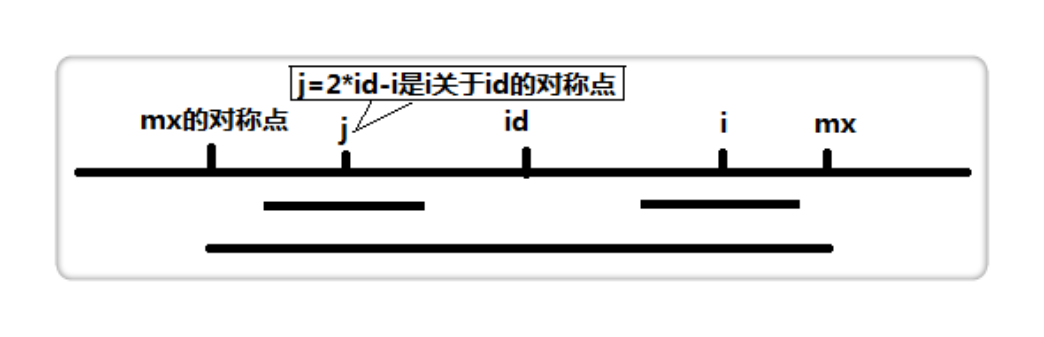
带有下划线的部分,是已经计算得出的回文串。
代码实现:

1 void Manache() { 2 int pos=0,mx=0; 3 for(register int i=1;i<=n;++i) { 4 len[i]=i<mx?min(len[(pos<<1)-i],mx-i):1; 5 while(b[i-len[i]]==b[i+len[i]]) len[i]++; 6 if(i+len[i]>mx) mx=i+len[i],pos=i; 7 } 8 }





 浙公网安备 33010602011771号
浙公网安备 33010602011771号