从【BZOJ4173】谈做题技巧

题目描述

-------------------------------------------------------------------------------------------------------------------------------------------

正常题解：

　　

 

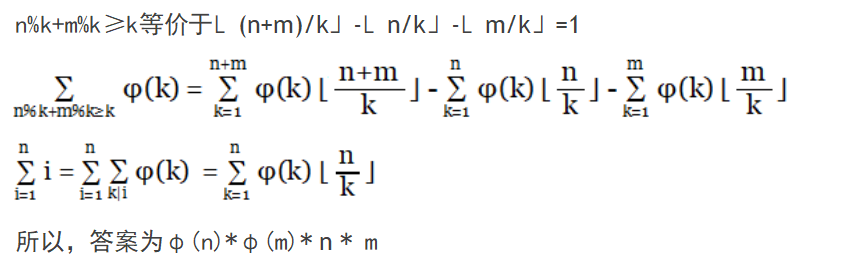
特别的做题技巧

　　我们一上来，先写一个打表程序，打出一系列n,m对应的答案。

　　我们发现，对于素数n,m 他们的答案总是(n-1)*n*(m-1)*m。

　　一开始，我们先稳了一个素数的情况，起码也得有20分吧！心态放好！

　　然后，我们来思考为什么素数有这样的性质：

　　　　如果你对欧拉函数有足够的了解的话，你会知道，对于一个素数P 他的欧拉函数是P-1

　　　　那么，刚才的M-1 N-1 实际上是欧拉函数，那么，对于和数是否也有这样的性质呢？

　　　　答案是显然的。

　　　　这就是计算机的优点，虽然无法给出正确证明，但是可以通过大量实验数据，得到一个令人信服的结论。

　　　　做题总耗时： 打表程序——2分钟，找规律——3分钟，写正解程序——5分钟。

　　　　一道难题就被我们10分钟干掉了。

　　　　信息学竞赛不应该是人类的拼命推理，推公式，而是人脑与计算机的完美结合。

 

　　　　附上正解代码

　　　　

#include<iostream>  
#include<cstdio>  
#define N 40000  
using namespace std;  
const unsigned long long int mod = 998244353;
int n,m;  
unsigned long long phi(unsigned long long x)
{
    unsigned long long int res = x,a = x;
    for(unsigned long long int i=2;i*i<=a;i++)
    {
        if(a%i==0)
        {
            res = res/i*(i-1);
            while(a%i==0)a/=i;
        }
    }
    if(a>1)res =res/a*(a-1);
    return res%mod;
}
unsigned long long a,b;
int main()  
{  
    scanf("%llu%llu",&a,&b);
    unsigned long long p1 = phi(a),p2=phi(b),ans=0;
    ans=p1%mod*p2%mod*(a%mod)%mod*(b%mod)%mod;
    printf("%llu",ans);
}