第5章 生产要素投入的决策分析

1 生产函数

1.1 生产函数的概念

1.1.1 生产要素

生产要素：指从事生产所必须投入的各种经济资源。

包括：土地、劳动、资本、企业家才能。

1.1.2 生产函数

生产函数：指在一定时期内，在技术水平不变的情况下，生产中所使用的各种生产要素的数量与所能生产的最大产量之间的关系。

生产函数的一般形式为：

Q=f（L，K，N，E）

注意：

1、一定技术条件为前提；

2、生产函数表明的是一定数量的生产要素所能产出的最大产量 。

 

 

 

 

 

1.2 常见的生产函数

1.2.1 柯布-道格拉斯生产函数

如果Q=2L^0.2K^0.5，则可以判断其规模报酬（递减）

α + β < 1  ， 递减

α + β = 1  ， 不变

α + β > 1  ， 递增

2 短期生产函数分析

2.1 短期和长期的区别

短期：在这个时期内，企业不能根据它所要达到的产量来调整其全部生产要素，只能调整部分可变要素。

长期：在这个时期内，企业可以根据它所要达到的产量来调整其全部生产要素，即企业的整个生产规模发生变化。

2.2 短期生产函数的概念

短期生产函数(单变量生产函数)：指企业在此期间内，只有一种投入要素的数量是可变的（如劳动力），其他投入要素的数量不变（如厂房、机器设备等）。

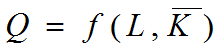
短期生产函数主要研究产出量与投入的变动要素之间的关系，以确定单一可变要素的最佳投入量。

2.3 总产量、平均产量和边际产量

2.3.1 概念

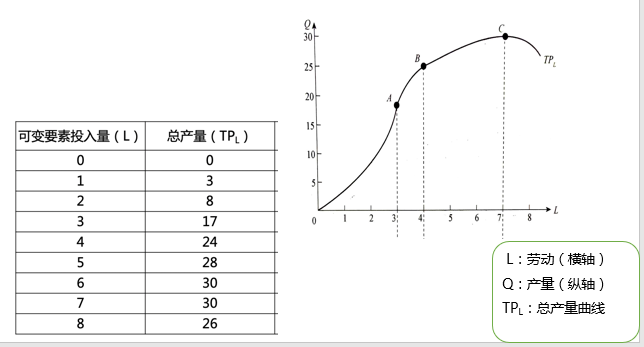
总产量（Total Product，TP）：一定量的某种生产要素所生产出来的全部产量。

例如：TP_L：指一定量的劳动投入所生产出来的全部产量，则：

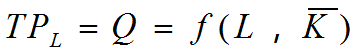
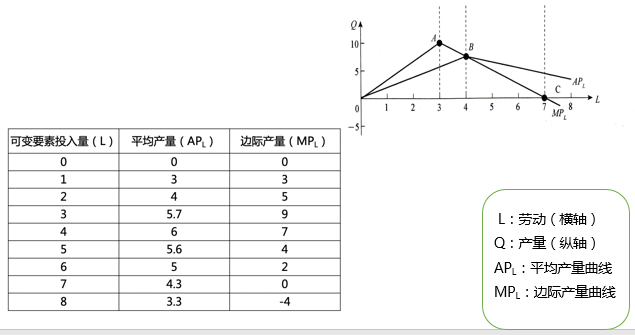
平均产量（Average Product ，AP）：指平均每单位某种生产要素所生产出来的产量。

例如：AP_L：指平均每单位劳动所生产出来的产量，则：

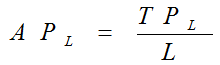
边际产量（Marginal Product，MP）：指某种生产要素每增加一单位所增加的产量。

例如：MP_L：指每增加一单位劳动所增加的产量，则 ：

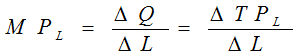
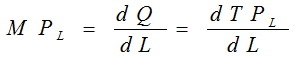
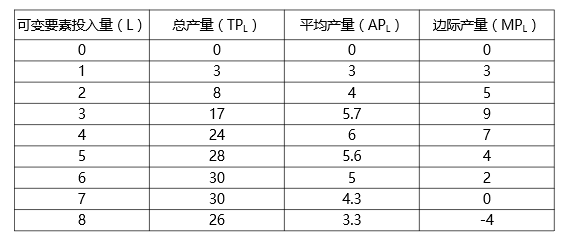
2.3.1.1 例题

重要结论：

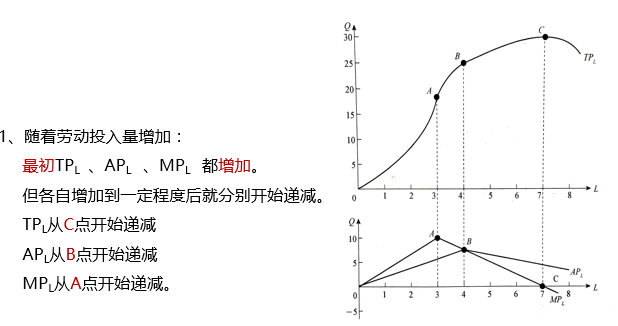
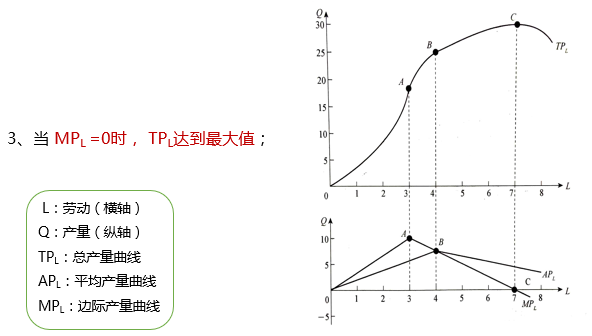
1、边际产量MP=0，总产量最大。

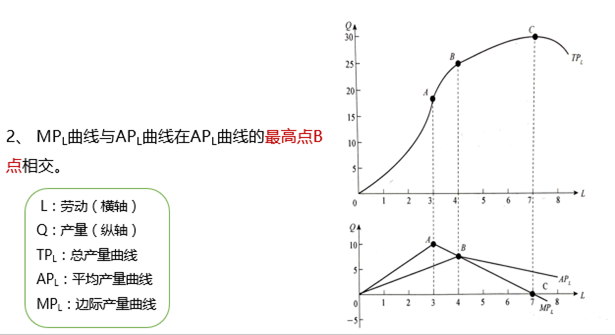
2、边际产量MP和平均产量AP相交的点：平均产量AP的最大值点。

2.4 边际收益递减规律

2.4.1 边际收益递减规律

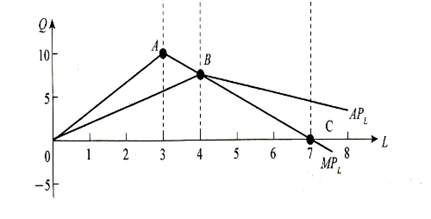
边际收益递减规律(报酬递减法则)：在技术水平不变的条件下，当把一种可变的生产要素连续地投入到生产中时，最初这种生产要素的增加会使边际产量增加，但当该生产要素的增加超过一定数量之后，继续增加该要素的投入，边际产量开始递减，最终还会使产量绝对减少。

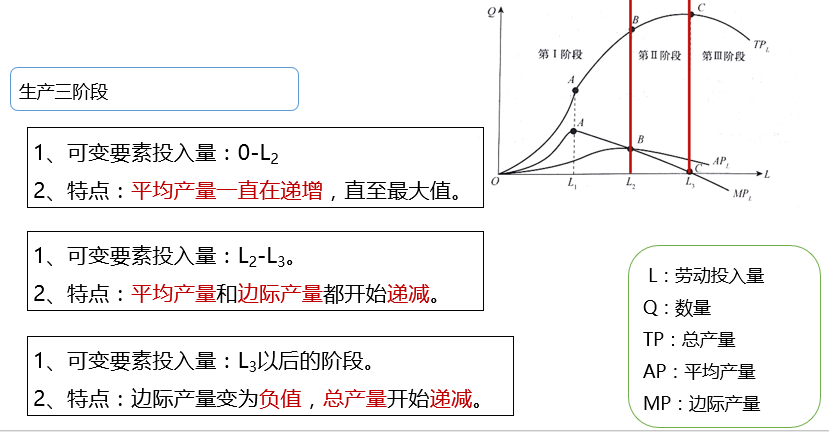
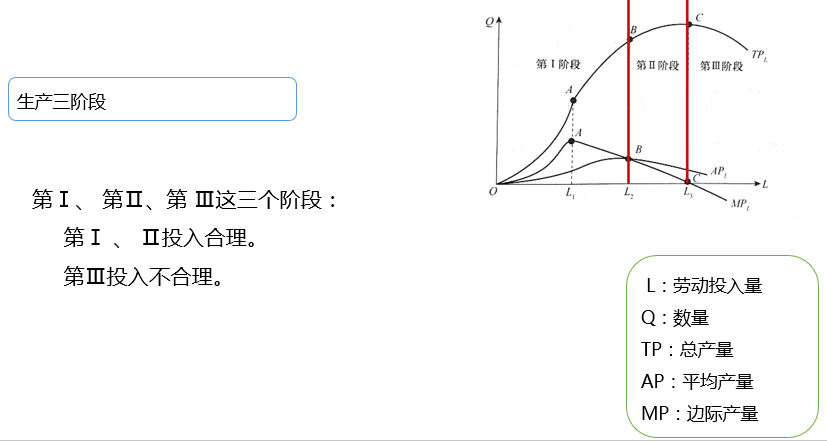
2.5 生产三阶段

2.5.1 第1阶段

2.5.2 第2阶段

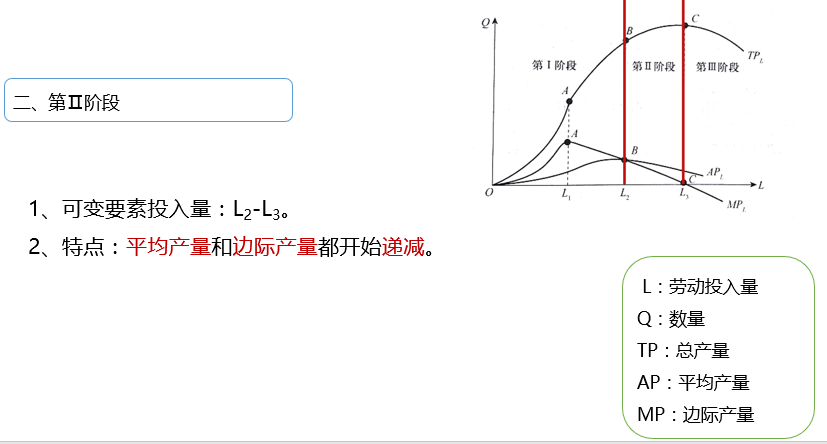
2.5.3 第3阶段

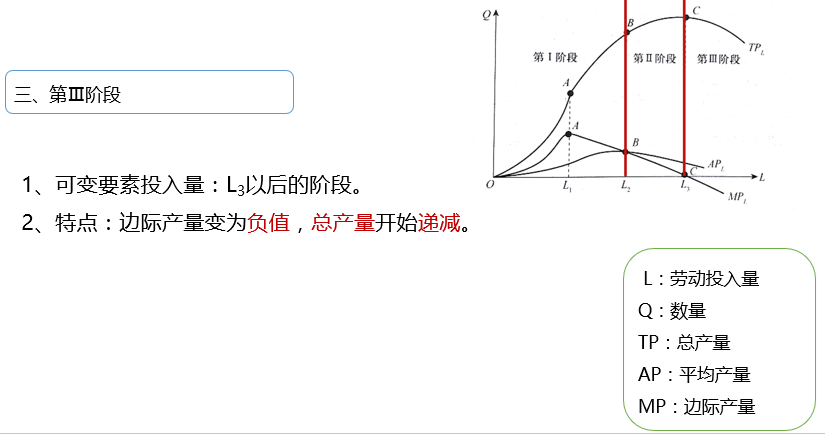
2.5.4 总结

2.6 一种生产要素变动时要素最佳投入量的确定

2.6.1 边际产品价值

边际产品价值（value of marginal product，VMP）：每增加一个单位某种可变生产要素所增加的收入。

2.6.2 生产要素的边际成本

生产要素的边际成本（marginal factor cost, MFC）：每增加使用一单位的某种可变生产要素所增加的成本。

2.6.3 一种生产要素变动时要素最佳投入量的确定

假定这种变动要素L的价格为P_L，并且假定要素的价格（P_L）固定不变，并且在企业诸多投入要素中，确定只有L要素是唯一的可变投入要素，则L生产要素的边际成本可以表示为：

边际产品价值(VMP)=变动要素的价格(P_L)

L：劳动

P：价格

3 长期生产函数分析

3.1 等产量曲线

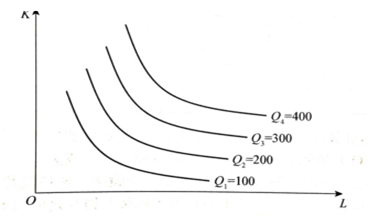
3.1.1 等产量曲线的概念

等产量曲线：在技术水平不变的条件下，生产同一产量的两种生产要素投入量的各种不同组合的轨迹。

3.1.2 等产量曲线的特点

1、向右下方倾斜的曲线。

2、在同一平面上可以有无数条等产量曲线，原点越远的等产量曲线所代表的产量水平越高。

3、在同一平面图上，任意两条等产量曲线不能相交。

4、等产量曲线的形状反映出两种投入要素的替代性。

5、等产量曲线是一条凸向原点的曲线，边际技术替代率递减所决定的。

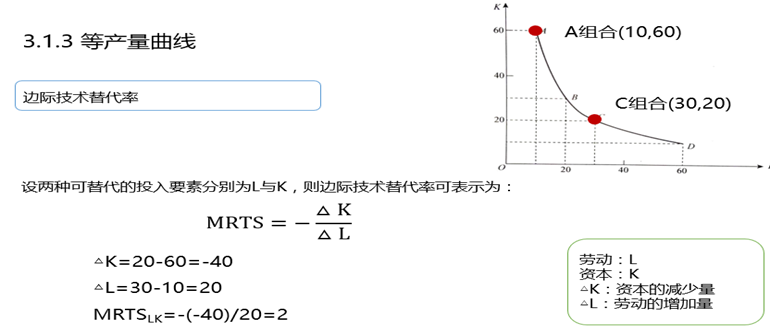
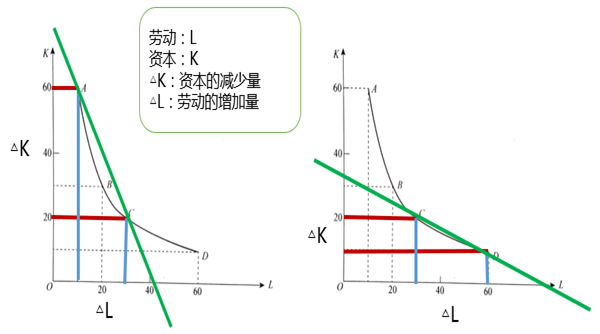
3.1.3 边际技术替代率

边际技术替代率(marginal rate of technical substitution，MRTS)，为了维持相同产量水平，增加一种生产要素的数量与可以减少的另一种生产要素的数量之比。

3.2 等成本线

3.2.1 等成本线的概念

等成本线：表明成本与生产要素价格既定的条件下，可以购买到的两种生产要素数量的最大组合的线。

3.2.2 等成本线的方程、斜率

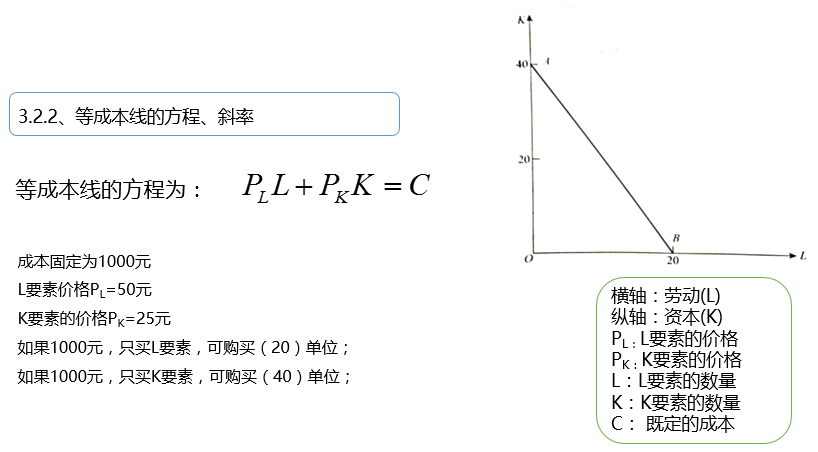
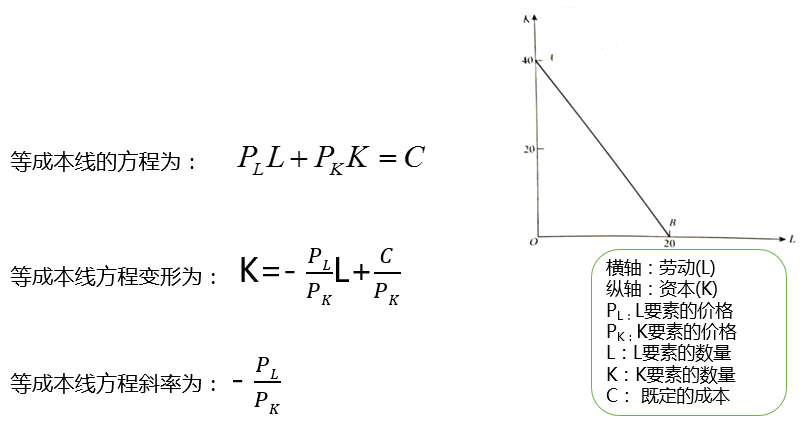
3.2.3 等成本线特征

1、要素价格不变，等成本线是一条直线。

2、投入成本增加，等成本线平行右移。

3、距离原点越远的等成本线表明支出的成本越高。

3.3 生产要素最佳组合的确定

3.3.1 生产要素最佳投入量的确定

生产要素的最佳组合：

情况一：选择一种要素投入的组合，使得企业能够在既定的产量下，所费成本最少；

情况二：选择一种要素投入的组合，使得在既定成本下，所生产的产量最大。

3.3.2 产量既定成本最小的要素组合

3.2.3 成本既定产量最大的要素组合

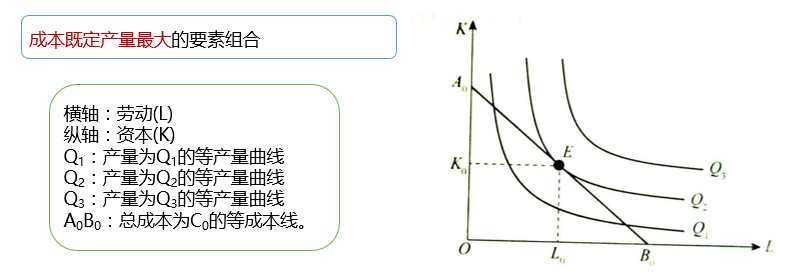
3.2.4 生产要素最佳组合原则

3.2.4.1 例题1

某车间男、女各一半，男工、女工可以相互替代，假定男工每增加1人可增产10件产品，女工每增加1人可增产8件产品。男工工资为每人4元，女工工资为每人2元，那么该车间男、女工比例是否合适？为什么？

男：MP_男=10，P_男=4

女：MP_女=8，P_女=2

MP_男/ P_男=10/4=2.5

MP_女/P_女=8/2=4

MP_男/ P_男＜ MP_女/P_女，男、女工组合比例未达到最优，这个比例是不合适的。

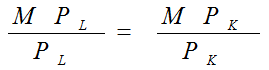
3.2.4.2 例题2

东兴农场种植苹果，据估计每月增加灌溉用水10吨，能使产量每月增加1500千克；或者每月增加肥料2吨，能使产量每月增加900千克。水的价格是每吨6元，肥料的价格为每吨25元。问该农场使用水和肥料的比例是否最优？如果不是最优，是应增加水、减少肥料，还是减少水、增加肥料？

MP_水=1500/10=150

P_水=6

MP_水/P_水=150/6=25

MP_肥料=900/2=450

P_肥料=25

MP_肥料/P_肥料=18

25＞18，不是最优，增加水，减少肥料。

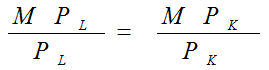
3.2.4.3 例题3

已知厂商的生产函数为Q=20L+10K-4L²-2K²，又设P₁（L的价格）=4元，P₂（K的价格）=2元，求成本为240时的最优生产要素组合。

MP_L：L要素的边际产量

P_L： L要素的价格

MP_K：K要素的边际产量

P_K： K要素的价格

4 规模报酬

4.1 规模报酬的含义

规模报酬：在一定的技术条件下，所有生产要素的投入都按同一比例变化，从而生产规模变动时所引起的产量或收益的变动。

第一阶段：规模报酬递增阶段。产量或收益增加的幅度大于各种要素投入增加的幅度。

第二阶段：规模报酬不变阶段。产量或收益增加的幅度等于各种要素投入增加的幅度。

第三阶段：规模报酬递减阶段。产量或收益增加的幅度小于各种要素投入增加的幅度。

适度规模的原则是绝对避免规模报酬递减

4.2 规模报酬变动的原因

1、技术方面的经济效果

2、管理方面的经济效果

3、商业方面的经济效果

4、金融方面的经济效果

5、承担风险方面的经济效果

金融才子运用技术管理手段控制商业风险。

5 生产函数与技术进步

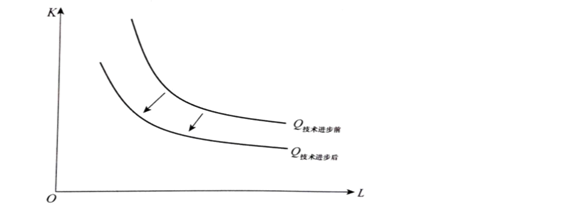
5.1 技术进步导致生产函数的改变

5.1.1 生产函数和技术进步的关系