马拉车和字典树

马拉车算法：用于求解最长回文子串的问题。因为它能够以O(n)的时间复杂度求解答案，因此十分的高效。

算法思想：马拉车算法主要是利用已求解的回文子串内部具有对称性，借由此来进行加速处理。

举个例子：

1.字符串：abbababa        最长回文子串：5（abbababa）

2.字符串：abcbbabbc      最长回文子串：7（abcbbabbc）

3.字符串：abccbaba        最长回文子串：6（abccbaba）

传统方法是，遍历每个字符，以该字符为中心向两边查找。时间复杂度为O(n^2)，效率很差；

在此基础上可以先对字符串哈希一下，然后用二分求解，可以达到O(nlogn)。

最后最优的求解此类问题的算法就是我们的马拉车算法了，他达到了神奇的O(n)。

回文串分为奇回文和偶回文，而我们的马拉车算法进行了一个骚操作，将所有回文子串都处理成了奇回文。我们在每个字符的前边和后边都插入一个没有出现过的字符，最后再在最前面插入一个没有出现过的字符（防止越界），就可以达到这个神奇的效果。

举个例子：

字符串：abbababa

变换之后：$#a#b#b#a#b#a#b#a#\0

回文子串：#a#, #a#b#a#b#a#

这样变换后的字符串中的回文子串就都变成了奇回文。

我们规定以s[i]为中心的回文子串的半径为p[i]，即回文子串的长度为2 * p[i] - 1，如上边#a#b#a#b#a#，回文半径为6，长度为11，还可以得出原字符串此时对应的回文子串长度为5，即p[i] - 1 = 6 - 1 = 5。

可以多画几个例子看看，这个是根据变换后字符串的规律得到的。

 

 

 那么，p[i]应该如何计算呢。

 

 

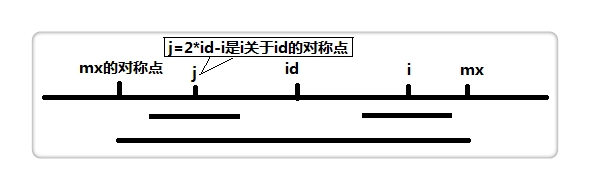
 我们计算的时候从左往右计算。由图我们可知此时p[j](j = 2 * id - i)已经计算出来了。图中表示现在(2 * id - mx, mx)区域内为一个回文子串，因此我们可以得知p[i] = p[j] (i < mx)，然后再循环检索一下以i为中心还能再扩大半径不，就可以求得p[i]，话不多说，上代码：

const int maxn = 2e6 + 7;
char s[maxn], a[maxn]; int p[maxn];
int Manacher(char s[], int len) {
    int l = 0;
    a[l++] = '$';
    a[l++] = '#';
    for (int i = 0; i < len; i++) {
        a[l++] = s[i];
        a[l++] = '#';
    }
    a[l] = 0;
    int mx = 0, id = 0, maxLen = -1;
    for (int i = 1; i < l - 1; i++) {
        p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
        while (a[i + p[i]] == a[i - p[i]]) p[i]++;
        if (i + p[i] > mx) mx = i + p[i], id = i;
        if (p[i] > maxLen) maxLen = p[i] - 1;
    }
    return maxLen;
}

 然我们来看看例题：

acwing： https://www.acwing.com/problem/content/141/

字典树：能够快速查询当前字符串是否出现过和其他相关问题。

算法思想：利用空间换取时间。预处理建一棵树，把内容都记录下来，如下：

 

 

（标橙色的节点是“目标节点“，即根节点到这个目标节点的路径上的所有字母构成了一个单词。）

字典树就是一棵树，树边记录了一些字符，结点记录了一些标记信息。

这就是字典树的概念。结合上面说的概念，上图所示的字典树包括的单词分别为：

a
abc
bac
bbc
ca

根据字典树的概念，我们可以发现：字典树的本质是把很多字符串拆成单个字符的形式，以树的方式存储起来。所以我们说字典树维护的是”字典“。那么根据这个最基本的性质，我们可以由此延伸出字典树的很多妙用。简单总结起来大体如下：

• 1、维护字符串集合（即字典）。

• 2、向字符串集合中插入字符串（即建树）。

• 3、查询字符串集合中是否有某个字符串（即查询）。

• 4、统计字符串在集合中出现的个数（即统计）。

• 5、将字符串集合按字典序排序（即字典序排序）。

• 6、求集合内两个字符串的LCP（Longest Common Prefix，最长公共前缀）（即求最长公共前缀）。

字典树的两种基本操作为建树和查询。

存储数据结构：

const int maxn = 2e5 + 7;
int trie[maxn][26], col[maxn], tot = 1;
char s[maxn];

其中，trie[i][j]表示一个指向子节点的指针，col[i]表示一个终止标记，tot记录现有的结点个数

插入操作：

void insert(char* s) {
    int len = strlen(s), p = 1;
    for (int i = 0; i < len; i++) {
        int k = s[i] - 'a';
        if (!trie[p][k]) trie[p][k] = ++tot;
        p = trie[p][k];
    }
    col[p] = 1;
}

查询操作：

bool search(char* s) {
    int len = strlen(s), p = 1;
    for (int i = 0; i < len; i++) {
        int k = s[i] - 'a';
        if (!trie[p][k]) return false;
        p = trie[p][k];
    }
    return col[p] == 1;
}

 来看看例题： https://www.acwing.com/problem/content/144/       https://www.acwing.com/problem/content/163/