数字图像处理的Matlab实现(1)—绪论
第1章 绪论
1.1 什么是数字图像处理
一幅图像可以定义为一个二维函数\(f(x,y)\),这里的\(x\)和\(y\)是空间坐标,而在任意坐标\((x,y)\)处的幅度\(f\)被称为这一坐标位置图像的亮度或灰度。当\(x\)、\(y\)和\(f\)的幅值都是有限的离散值时,称图像为数字图像。数字图像由有限数量的元素组成,每个元素都有特殊的位置和数值,这些元素称为画像元素、图像元素和像素。像素时定义数字图像元素时使用最广泛的术语.
图像处理和计算机视觉之间并没有清晰的划分界限:
- 低级处理:输入和输出通常都是图像。比如降低噪声的图像预处理、对比度增强和图像锐化。
- 中级处理:输入通常是图像,输出则是从这些图像中提取的特征(如边缘、轮廓和单个目标的特征),典型应用是图像分割,对目标进行描述,把它们缩减为适合计算机处理的形式,并对单个目标进行分类。
- 高级处理:对识别的目标进行总体了解,执行与人类视觉相关的认知功能
1.2 数字图像的表示
一幅图像可以被定义为一个二维函数\(f(x,y)\),其中\(x\)和\(y\)是空间(平面)坐标,在任何坐标\((x,y)\)处的幅度\(f\)被称为图像在这一位置的亮度。“灰度”通常是用来表示黑白图像亮度的术语,彩色图像是由独立的图像组合而形成的。例如,在RGB彩色系统中,一幅彩色图像是由称为红、绿、蓝原色图像的3幅独立的单色图像组成的。因此,许多为黑白图像处理开发的技术也适用于彩色图像处理,方法是分别处理3幅独立的分量图像即可。
图像在\(x\)和\(y\)坐标,以及幅度上是连续的,要将这样的一幅图像转换成数字的形式,要求对坐标和幅度进行数字化。将坐标值数字化称为取样,将幅值数字化称为量化。当\(x\)、\(y\)分量及幅值\(f\)都是有限且离散的量时,我们称图像为数字图像。
1.2.1 坐标约定
取样和量化的结果是实数矩阵。假设对一幅图像\(f(x,y)\)进行采样后,可得到一幅\(M\)行、\(N\)列的图像,则称图像的大小是\(M\times N\)。相应的值是离散的,为使符号清晰和方便起见,这些离散的坐标都取整数。在很多图像处理书籍中,图像的原点被定义为\((x,y)=(0,0)\)。图像中沿着第1行的下一坐标点是\((x,y)=(0,1)\)。符号\((0,1)\)用来表示沿着第一行的第2个取样。当图像被取样时,并不意味着在物理坐标系中存在实际值,\(x\)是从\(0\)到\(M-1\)的整数,\(y\)是从\(0\)到\(N-1\)的整数。
1.2.2 图像的矩阵表示
根据上述坐标系统,数字图像的矩阵表示为:
\[f(x,y)=\begin{bmatrix}f(0,0) & f(0,1) & \cdots & f(0,N-1)\\
f(1,0) & f(1,1) & \cdots & f(1,N-1)\\
\cdots & \cdots & \cdots & \cdots\\
f(M-1,0) & f(M-1,1) & \cdots & f(M-1,N-1)\end{bmatrix}\]
等式右边是定义的一幅数字图像。阵列的每个元素都被称作图像元素、图画元素或像素。
可将数字图像表示成MATLAB矩阵:
\[\mathtt{f}=\begin{bmatrix}\mathtt{f(1,1)} & \mathtt{f(1,2)} & \cdots & \mathtt{f(1,N)}\\
\mathtt{f(2,1)} & \mathtt{f(2,2)} & \cdots & \mathtt{f(2,N)}\\
\cdots & \cdots & \cdots & \cdots\\
\mathtt{f(M,1)} & \mathtt{f(M,2)} & \cdots & \mathtt{f(M,N)}\end{bmatrix}\]
其中,\(\mathtt{f(1,1)}=f(0,0)\),除了原点的平移之外,其他都是相同的。符号 \(\mathtt{f(p,q)}\) 表示第 \(\mathtt{p}\) 行、第 \(\mathtt{q}\) 列的元素。
1.3 图像的输入/输出和显示
可以使用函数imread将图像读入MATLAB环境,imread的基本语法是:
imread('filename')
此处,filename是含有图像文件全名的字符串(包括任何可用的扩展名)
使用imshow函数在MATALB桌面显示图像,imshow的基本语法是:
imshow(f)
其中,f是图像数组。下面的语句表示从磁盘读取名为rose_512.tif的图像并用imshow函数进行显示:
>> f=imread('rose_512.tif');
>> imshow(f)
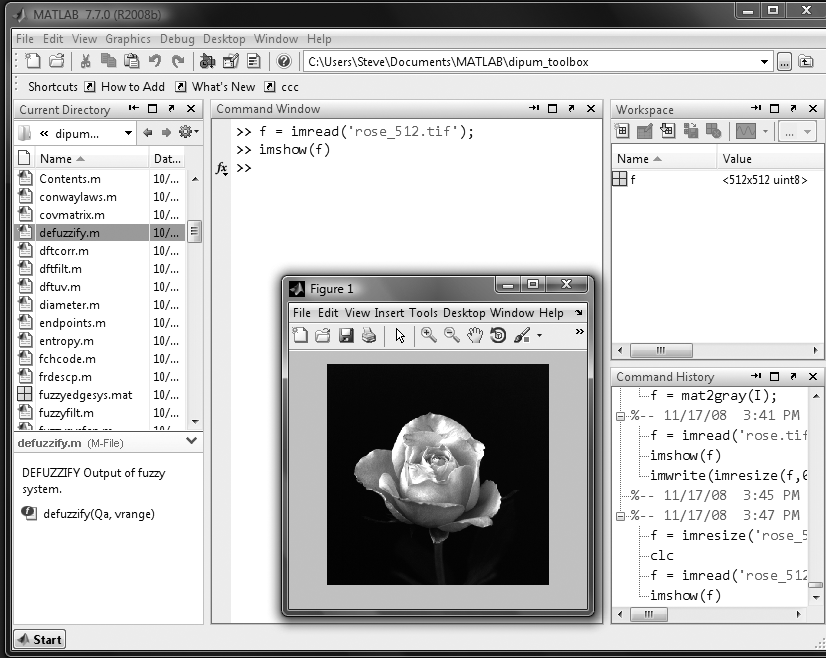
上图显示了在屏幕上的输出。注意,图窗编号出现在最终得到的图窗的左上部。如果另一幅图像g随后用imshow来显示,MATLAB就用新图像取代图窗中的图像。为了保留第1幅图像并输出第2幅图像,可使用figure函数
figure,imshow(g)
使用imwrite函数将图像写入当前目录,imwrite的基本语法:
imwrite(f,'filename')
函数imwirte还可以有其他参数,具体取决于要写入的文件的格式。一种常用的但仅适用于JPEG图像的imwrite语法是:
imwrite(f,'filename.jpg','quality',q)
其中,q是介于0到100的整数(源于JPEG压缩,q越小,图像的退化就越严重)。仅适用于TIFF图像的更常用的imwrite语法如下:
imwrite(g,'filename.tif','compression','parameter','resolution',[colres rowres])
其中,parameter 可以采用下列取值:'none'(指出没有压缩)、'packbits'(默认的非二值图像)、'lwz'、‘deflate’、'jpeg'、'ccitt'(仅针对二值图像,为默认值)、'fax3'(仅针对二值图像)和'fax4'。\(1\times 2\)数组[colres rowres]包含两个整数,以每单位点数给出列分辨率和行分辨率(默认值是[72 72])。例如,如果图像的维数以英寸计,那么colres是垂直方向上每英寸的点数,同样,rowres是水平方向上的每英寸的点数。
1.4 类和图像类型
虽然用的是整数坐标,但MATLAB中的像素值并未限制为整数,下表给出了MATLAB和图像处理工具箱为描述像素值而支持的各种类。
| 名称 | 描述 | |
|---|---|---|
| double | 双精度浮点数,范围为\(\pm10^{308}\),(每像素8个字节) | |
| single | 单精度浮点数,范围为\(\pm10^{38}\), (每像素4个字节) | |
| uint8 | 无符号8比特整数,范围为\([0,255]\),(每像素1个字节) | |
| uint16 | 无符号16比特整数,范围为\([0,2^{16}-1]\),(每像素2个字节) | |
| uint32 | 无符号32比特整数,范围为\([0,2^{32}-1]\),(每像素4个字节) | |
| int8 | 有符号8比特整数,范围为\([-128,127]\),(每像素1个字节) | |
| int16 | 有符号16比特整数,范围为\([-2^{15},2^{15}-1]\),(每像素2个字节) | |
| int32 | 有符号32比特整数,范围为\([-2^{31},2^{31}-1]\),(每像素4个字节) | |
| char | 字符,(每像素2个字节) | |
| logical | 值为0或1 (每像素1个字节) |
uint8 和 logical 类广泛用于图像处理,当以TIFF或JPEG图像文件格式读取图像时,会用到这两个类。这两个类用1个字节表示每个像素。某些科研数据源,比如医学成像,要求提供超过uint8的动态范围,针对此类数据,会采用uint16和int16类,这两个类为每个矩阵元素使用2个字节。针对计算灰度的操作,比如傅里叶变换,使用double和single浮点类。双精度浮点数为每个数组元素使用8个字节,而单精度浮点数使用4个字节。
工具箱支持4种图像类型:
- 灰度图像
- 二值图像
- 索引图像
- RGB图像
1.4.1 灰度图像
灰度图像是数据矩阵,矩阵的值表示灰度浓度,当灰度图像的元素是uint8或uint16类时,它们分别具有范围\([0,255]\)或\([0,65535]\)的整数值。如果图像是double或single类,值就是浮点数。double或single灰度图像额值通常被归一化标定为\([0,1]\)范围内。
1.4.2 二值图像
二值图像在MATLAB中具有非常特殊的意义,二值图像是取值只有0和1的逻辑数组。因而,只包含0和1数据类的数组,比如uint8,在MATLAb中并不认为是二值图像。用logical函数可以把数值数组转换为二值图像。因此,如果A是由0和1构成的数值数组,就可以使用下列语句创建逻辑数组B:
B=logical(A)
如果A中含有除了0和1之外的其他元素,使用logical函数就可以将所有非0值变换为逻辑1,而将所有0值变换为逻辑0。可使用函数islogical 来测试数组是否为逻辑类:
islogical(C)
如果C是逻辑数组,此函数将返回1,否则返回0。使用通常的类转换语法,可以将逻辑数组转换为数值数组:
B=class_name(A)
其中,class_name是im2uint8、im2uint16、im2double、im2single 或mat2gray。工具箱函数mat2gray可以将图像转换为标定为\([0,1]\)范围的double类的数组:
g=mat2gray(A,[Amin,Amax])
其中,图像g具有范围为0(黑)到1(白)的值。特定参数Amin和Amax使得A中小于Amin的值,在g中变为0;而在A中大于Amax的值,在g中变为1。另外一种语法是:
g=mat2gray(A)




