数值计算day2-求解非线性方程
上节课介绍了计算机中浮点数的表示方法,数值计算中涉及到的几种误差以及数值方法这门课中的一些数学基础。本节课将介绍如果使用数值方法来求解非线性方程。
1. MATLAB基本操作
>> % 生成序列
>> 1:5
ans =
1 2 3 4 5
>> % 清空所有变量,在脚本执行之前调用
>> clear all
>> % 函数定义方式1,在脚本文件中定义
function y = name(x)
... (commands)
end
>> % 函数定义方式2,函数句柄
>> f=@(x) x.^2
2. 应用背景
实际中,很多方程无法写出解析解,比如:\(e^x+sinx*x^5 = 900\)

上图中,阴影部分的面积为\(A = \frac{1}{2}r^2\theta-\frac{1}{2}r^2sin\theta\),给定\(A=8m^2\), \(r=3m\),求解对应的\(\theta\),即\(f(\theta) = 8-4.5(\theta-sin\theta) = 0\),无法得出解析解,MATLAB中,可以使用fzero计算出一个数值解:
>> f=@(x) 8-4.5*(x-sin(x))
f =
包含以下值的 function_handle:
@(x)8-4.5*(x-sin(x))
>> fzero(f,0)
ans =
2.4305
>> format long
>> fzero(f,0)
ans =
2.430465741723630
通常,求解非线性方程的方法有两类:一类是交叉法(bracketing methods),一类是开放法(open methods)。在交叉法中,先确定解所在的一个区间,利用数值算法,不断缩小该区间,直到区间两端点之间的距离小于一个给定的精度。在开放法中,通常先给出解的一个估计值,再利用数值算法,得出一个更精确的解。

3. 数值解误差估计
在介绍一些数值解法之前,先介绍在数值解中误差的几种估计。由于数值解并不是真实解,因此必须使用一些误差估计原则来确定数值解的真实程度。假设\(x_{TS}\)是\(f(x)=0\)真实解,即\(f(x_{TS})=0\),\(x_{NS}\)为数值估计解,\(f(x_{NS}) = \epsilon\),有如下四种对误差的度量方式:
- 真实误差(True error):\(TrueError = x_{TS}-x_{NS}\),真实误差难以计算,因为通常无法得到真实解
- \(f(x)\)的差值(Tolerance in \(f(x)\)):\(ToleranceInf = |f(x_{TS})-f(x_{NS})|=|0-\epsilon|=|\epsilon|\)
- 解的差值(Tolerance in \(x\)):假设已知\(x_{TS}\) 在区间\([a,b]\)之间,取\(\frac{a+b}{2}\)为数值解\(x_{NS}\),则真实解与数值解的差值满足:\(|x_{TS}-x_{NS}|<\frac{b-a}{2}\)
- 相对误差(Relative error):$$TrueRelativeError = |\frac{x_{TS}-x_{NS}}{x_{TS}}|,EstimatedRelativeError = |\frac{x{(n)}_{NS}-x{NS}}{x^{(n-1)}{NS}}|$$
4. 交叉法
4.1 二分法(Bisection method,依赖于介值定理)
给定区间\([a,b]\),假设\(f(x)\)连续且\(f(x)=0\)在该区间上有解。此时,\(f(x)\)在区间的那两个端点必定异号,即\(f(a)>0,f(b)<0\),或者\(f(a)<0,f(b)>0\),换句话说,如果\(x=a\)与\(x=b\)之间有一个解,则\(f(a)f(b)<0\)。

算法步骤:
- \(f(a)f(b)<0\), 取\(x_{NS}=\frac{a+b}{2}\)
- 如果\(f(x_{NS})=0\),算法停止;如果\(f(a)f(x_{NS})<0\),则令\(a:= a, b: = x_{NS}\);如果\(f(b)f(x_{NS})<0\),则令\(a:= x_{NS}, b:= b\)
- 使用Tolerance in \(x\) 来决定停止准则,给定\(\epsilon>0\),当\(\frac{b-a}{2}<\epsilon\)时,停止
二分法的优缺点:
- 二分法总会收敛到一个解
- \(f(x)\)不穿过X轴时,无法使用
- 收敛速度较慢
MATLAB实现:
clear all
F = inline('8-4.5*(x-sin(x))');
a = 2; b = 3; imax = 20; tol = 0.001;
Fa=F(a); Fb=F(b);
if Fa*Fb > 0
disp('Error: The function has the same sign at points a and b.')
else
disp('iteration a b (xNS) Solution f(xNS) Tolerance')
for i = 1:imax
xNS = (a + b)/2;
toli=abs((b-a)/2);
FxNS=F(xNS);
fprintf('%3i %11.6f %11.6f %11.6f %11.6f %11.6f\n',i, a, b, xNS, FxNS, toli)
if FxNS == 0
fprintf('An exact solution x =%11.6f was found',xNS)
break
end
if toli < tol
break
end
if i == imax
fprintf('Solution was not obtained in %i iterations',imax)
break
end
if F(a)*FxNS < 0
b = xNS;
else
a = xNS;
end
end
end
% 运行结果
>> Program_3_1
iteration a b (xNS) Solution f(xNS) Tolerance
1 2.000000 3.000000 2.500000 -0.556875 0.500000
2 2.000000 2.500000 2.250000 1.376329 0.250000
3 2.250000 2.500000 2.375000 0.434083 0.125000
4 2.375000 2.500000 2.437500 -0.055709 0.062500
5 2.375000 2.437500 2.406250 0.190661 0.031250
6 2.406250 2.437500 2.421875 0.067838 0.015625
7 2.421875 2.437500 2.429688 0.006154 0.007813
8 2.429688 2.437500 2.433594 -0.024755 0.003906
9 2.429688 2.433594 2.431641 -0.009295 0.001953
10 2.429688 2.431641 2.430664 -0.001569 0.000977
4.2 线性插值法(Regula Falsi Method, 试位法)
将两点\((a,f(a)),(b,f(b))\)之间的连线与\(X\)轴的交点作为估计点:

给定区间\([a,b]\),\((a,f(a))\)与\((b,f(b))\)之间连线的方程为$$y=\frac{f(b)-f(a)}{b-a}(x-b)+f(b)$$ 令\(y=0\),得$$x_{NS} = \frac{af(b)-bf(a)}{f(b)-f(a)}$$ 后续的算法过程与二分法一致。
MATLAB中的fzero函数就是采用以上两种交叉法求解非线性方程的,而对于多项式方程$$a_nxn+a_{n-1}x+...+a_1x+a_0=0$$
MATLAB提供如下命令来进行求解:
root([a_n a_{n-1} ... a_1 a_0])
>> roots([1 2 -3])
ans =
-3.0000
1.0000
5. 开放法
5.1 牛顿法(Newton's method)
对连续可导函数\(f(x)\),假设知道\(f(x)=0\)在一个给定点附近有一个解,则可以使用牛顿法来估计解:

首先选取一个点\(x_1\)作为解的初始估计值,第二个估计点\(x_2\)通过取\(f(x)\)在点\((x_1,f(x_1))\)处的切线与\(X\)轴的交点得到,同理得到后续的估计点。注意,在第一次迭代过程中,斜率$$f'(x_1)=\frac{f(x_1)-0}{x_1-x_2}$$ 因此,$$x_2 = x_1-\frac{f(x_1)}{f'(x_1)}$$ 于是牛顿迭代法可以写出如下通解形式:$$x_{i+1}=x_i=\frac{f(x_i)}{f'(x_i)}$$
停机准则:牛顿法通常使用估计值的相对误差来作为停止条件 $$|\frac{x_{i+1}-x_i}{x_i}|\leq \epsilon$$
牛顿法的优缺点:
- 给定一个比较好的初始估计,算法收敛速度会很快
- 初始估计不够好,则无法保证算法会收敛

- 当函数的导数无法给出解析式时,需要设计求导算法
例:方程\(\frac{1}{x}-2=0\)的解为\(x=0.5\),使用牛顿法求解:
迭代公式为:$$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}=x_n-\frac{\frac{1}{x_n}-2}{\frac{1}{x_n2}}=x_n+x_n2(\frac{1}{x_n}-2)=x_n+x_n-2x_n^2=2x_n(1-x_n)$$
- \(x_1=1.4\), \(x_2 = 2*1.4*(-0.4)=-1.12\), \(x_3=2*x_2(1-x_2)=-4.7488\),不收敛
- \(x_1=1\), \(x_2 = 2*1*0=0\),\(x_3=2*0*1=0\),收敛到\(0\),\(0\)不是解
- \(x_1=0.4\), \(x_2=2*0.4*0.6=0.48\),\(x_3=2*0.48*(1-0.48)=0.4992\),收敛
MATLAB实现
function Xs = NewtonRoot(Fun,FunDer,Xest,Err,imax)
% NewtonRoot finds the root of Fun = 0 near the point Xest using Newton's method.
% Input variables:
% Fun Handle of a user-defined function that calculates Fun for a given x.
% FunDir Handle of a user-defined function that calculates the derivative
% of Fun for a given x.
% Xest Initial estimate of the solution.
% Err Maximum error.
% imax Maximum number of iterations
% Output variable:
% Xs Solution
for i = 1:imax
Xi = Xest - Fun(Xest)/FunDer(Xest);
if abs((Xi - Xest)/Xest) < Err
Xs = Xi;
break
end
Xest = Xi;
end
i
if i == imax
fprintf('Solution was not obtained in %i iterations.\n',imax)
Xs = ('No answer');
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
>> format long
>> f=@(x) 8-4.5*(x-sin(x))
f =
包含以下值的 function_handle:
@(x)8-4.5*(x-sin(x))
>> fder=@(x) -4.5*(1-cos(x))
fder =
包含以下值的 function_handle:
@(x)-4.5*(1-cos(x))
>> NewtonRoot(f,fder,2,1e-6,100)
i =
4
ans =
2.430465741723630
5.2 割线法(Secant method)
割线法使用两个与解临近的初始点来估计一个新的解。假设初始点为\(x_1\),\(x_2\),穿过这两个点的直线与\(X\)轴的交点就被作为新的估计值\(x_3\),这两个初始点的可以在解的同侧,也可以在不同侧:

穿过\((x_1,f(x_1))\)与\((x_2,f(x_2))\)的直线满足:$$\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{f(x_2)-0}{x_2-x_3}$$ 因此,$$x_3=x_2-\frac{f(x_2)(x_1-x_2)}{f(x_1)-f(x_2)}$$ 不断迭代下去,迭代公式为:$$x_{i+1}=x_i-\frac{f(x_i)(x_{i-1}-x_i)}{f(x_{i-1})-f(x_i)}$$ 
MATLAB实现:
function Xs = SecantRoot(Fun,Xa,Xb,Err,imax)
% SecantRoot finds the root of Fun = 0 using the Secant method.
% Input variables:
% Fun Name of a user-defined function that calculates Fun for a given x.
% a, b Two points in the neighborhood of the root (on either side, or the
% same side of the root).
% Err Maximum error.
% imax Maximum number of iterations
% Output variable:
% Xs Solution
for i = 1:imax
FunXb = Fun(Xb);
Xi = Xb - FunXb*(Xa-Xb)/(Fun(Xa)-FunXb);
if abs((Xi - Xb)/Xb) < Err
Xs = Xi;
break
end
Xa = Xb;
Xb = Xi;
end
if i == imax
fprintf('Solution was not obtained in %i iterations.\n',imax)
Xs = ('No answer');
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
>> format long
>> f=@(x) 8-4.5*(x-sin(x))
f =
包含以下值的 function_handle:
@(x)8-4.5*(x-sin(x))
>> SecantRoot(f,2,3,0.0001,10)
ans =
2.430465726588755
5.3 固定点迭代法(Fixed-point iteration method)
使用固定点迭代法求解方程的需要将方程改写为:$$x=g(x)$$ 最简单的改写方法是 \(f(x)=0 \rightarrow x = f(x)+x=g(x)\) ,显然若\(x\)是\(f(x)=0\)的解,则必有\(x=g(x)\),改写后得到的方程可以通过绘图来求解:

两条线的交点称作是固定点(Fixed point),初始估计点取在固定点附近,下一步则将\(g(x)\)的值作为新的估计值,一直迭代下去:$$x_{i+1}=g(x_i)$$

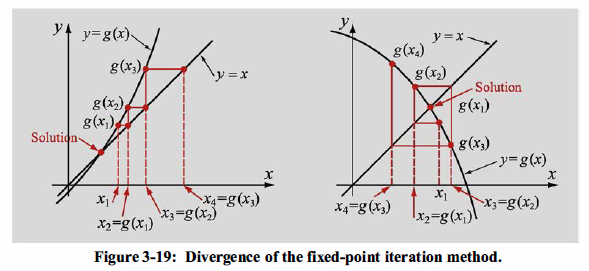
在固定点迭代法中,迭代函数不是唯一的,有的迭代函数可能导致方法不收敛,固定点收敛的条件为:\(|g'(x)|<1\text{(lipschitz 条件)}\)

例:\(xe^{0.5x}+1.2x-5=0\),使用固定点法求解(\(x=1,x=2\))
- \(1.2x=5-xe^{0.5x}\) $$x=\frac{5-xe^{0.5x}}{1.2}=g(x)$$ 此时\(g'(x)=-(e^{0.5x}+0.5xe^{0.5x})/1.2\),\(g'(1)=-2.0609,g'(2)=-4.5305\),算法不收敛 $$x_2 = \frac{5-1e{0.5}}{1.2}=2.7927,x_3=\frac{5-2.7927e{0.52.7927}}{1.2}=-5.2364$$ $$x_4=\frac{5-(-5.2364)e{0.5*(-5.2364)}}{1.2}=4.4849,x_5=\frac{5-4.4849e{0.54.4849}}{1.2}=-31.0262$$
- \(x(e^{0.5x}+1.2)=5\) $$x=\frac{5}{e^{0.5x}+1.2}=g(x)$$ \(g'(x)=\frac{-5e^{0.5x}}{2(e^{0.5x}+1.2)^2}\), \(g'(1)=-0.5079,g'(2)=-0.4426\),算法收敛 $$x_2=\frac{5}{e{0.5}+1.2}=1.7552,x_3=\frac{5}{e{0.51.7552}+1.2}=1.3869$$ $$x_4=\frac{5}{e{0.5*1.3869}+1.2}=1.5622,x_5=\frac{5}{e{0.51.5622}+1.2}=1.4776$$ $$x_6=\frac{5}{e{0.5*1.4776}+1.2}=1.5182,x_7=\frac{5}{e+1.2}=1.4986$$
- \(xe^{0.5x}=5-1.2x\) $$x=\frac{5-1.2x}{e^{0.5x}}$$ \(g'(x)=\frac{-3.7+0.6x}{e^{0.5x}}\),\(g'(1)=-1.8802,g'(2)=-0.9197\),算法不收敛
初始点可以通过画图进行估计:
>> f=@(x) x.*exp(0.5*x)+1.2*x-5
f =
包含以下值的 function_handle:
@(x)x.*exp(0.5*x)+1.2*x-5
>> x = linspace(0,3,100);
>> plot(x,f(x))
>> xlabel('x');
>> ylabel('f(x)');
>> title('f(x)=xe^{x/2}+1.2x-5');

6. 总结
本节课主要介绍了求解非线性方程的几种方法,主要分为两类,一类是交叉法,包括二分法、线性插值法,这类方法的停止条件通常采用解的差值准则;一类是开放法,包括牛顿法、割线法以及固定点法,这类方法的停止准则主要采用估计值的相对误差来规定。




