机器学习技法9-Decision Tree
注:
文章中所有的图片均来自台湾大学林轩田《机器学习技法》课程。
笔记原作者:红色石头
微信公众号:AI有道
上节课主要介绍了Adaptive Boosting。AdaBoost演算法通过调整每笔资料的权重,得到不同的hypotheses,然后将不同的hypothesis乘以不同的系数\(\alpha\)进行线性组合。这种演算法的优点是,即使底层的演算法\(g\)不是特别好(只要比乱选好点),经过多次迭代后算法模型会越来越好,起到了boost提升的效果。本节课将在此基础上介绍一种新的aggregation算法:决策树(Decision Tree)。
1. Decision Tree Hypothesis
从第7节课开始,我们就一直在介绍aggregation model。aggregation的核心就是将许多可供选择使用的比较好的hypothesis融合起来,利用集体的智慧组合成\(G\),使其得到更好的机器学习预测模型。下面,我们先来看看已经介绍过的aggregation type有哪些。
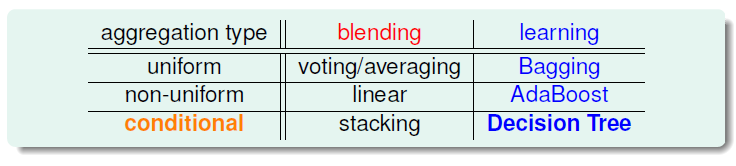
aggregation type有三种:uniform,non-uniform,conditional。它有两种情况,一种是所有的\(g\)是已知的,即blending。对应的三种类型分别是voting/averaging,linear和stacking。另外一种情况是所有\(g\)未知,只能通过手上的资料重构g,即learning。其中uniform和non-uniform分别对应的是Bagging和AdaBoost算法,而conditional对应的就是我们本节课将要介绍的Decision Tree算法。
决策树(Decision Tree)模型是一种传统的算法,它的处理方式与人类思维十分相似。例如下面这个例子,对下班时间、约会情况、提交截止时间这些条件进行判断,从而决定是否要进行在线课程测试。如下图所示,整个流程类似一个树状结构。
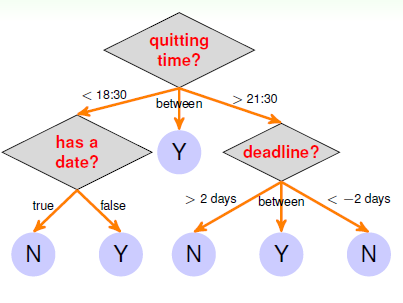
图中每个条件和选择都决定了最终的结果,Y or N。蓝色的圆圈表示树的叶子,即最终的决定。
把这种树状结构对应到一个hypothesis \(G(x)\)中,\(G(x)\)的表达式为:$$ G(x)=\sum_{t=1}^Tq_t(x)*g_t(x)$$ \(G(x)\)由许多\(g_t(x)\)组成,即aggregation的做法。每个\(g_t(x)\)就代表上图中的蓝色圆圈(树的叶子)。这里的\(g_t(x)\)是常数,因为是处理简单的classification问题。我们把这些\(g_t(x)\)称为base hypothesis。\(q_t(x)\)表示每个\(g_t(x)\)成立的条件,代表上图中橘色箭头的部分。不同的\(g_t(x)\)对应于不同的\(q_t(x)\),即从树的根部到顶端叶子的路径不同。图中的菱形代表每个简单的节点。所以,这些base hypothesis和conditions就构成了整个\(G(x)\)的形式,就像一棵树一样,从根部到顶端所有的叶子都安全映射到上述公式上去了。
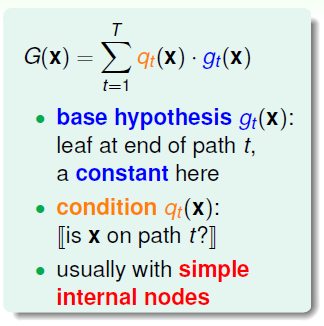
决策树实际上就是在模仿人类做决策的过程。一直以来,决策树的应用十分广泛而且分类预测效果都很不错,而它在数学上的理论完备性尚不充分,倒也不必在意。
如果从另外一个方面来看决策树的形式,不同于上述\(G(x)\)的公式,我们可以利用条件分支的思想,将整体\(G(x)\)分成若干个\(G_c(x)\),也就是把整个大树分成若干个小树,如下所示: $$G(x)=\sum^C_{c=1}[b(x)=c]*G_c(x)$$ 上式中,\(G(x)\)表示完整的大树,即full-tree hypothesis,\(b(x)\)表示每个分支条件,即branching criteria,\(G_c(x)\)表示第\(c\)个分支下的子树,即sub-tree。这种结构被称为递归型的数据结构,即将大树分割成不同的小树,再将小树继续分割成更小的子树。所以,决策树可以分为两部分:root和sub-trees。

在详细推导决策树算法之前,我们先来看一看它的优点和缺点。首先,decision tree的优点有:
- 模型直观,便于理解,应用广泛
- 算法简单,容易实现
- 训练和预测时,效率较高
然而,decision tree也有相应的缺点:
- 缺少足够的理论支持
- 如何选择合适的树结构对初学者来说比较困惑
- 决策树代表性的演算法比较少

2. Decision Tree Algorithm
我们可以用递归形式将decision tree表示出来,它的基本的算法可以写成:
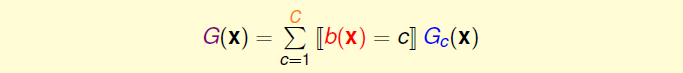
这个Basic Decision Tree Algorithm的流程可以分成四个部分,首先学习设定划分不同分支的标准和条件是什么;接着将整体数据集\(D\)根据分支个数\(C\)和条件,划为不同分支下的子集\(D_c\);然后对每个分支下的\(D_c\)进行训练,得到相应的机器学习模型\(G_c\);最后将所有分支下的\(G_c\)合并到一起,组成大矩\(G(x)\)。但值得注意的是,这种递归的形式需要终止条件,否则程序将一直进行下去。当满足递归的终止条件之后,将会返回基本的hypothesis \(g_t(x)\)。
所以,决策树的基本演算法包含了四个选择:
- 分支个数(number of branches)
- 分支条件(branching criteria)
- 终止条件(termination criteria)
- 基本算法(base hypothesis)
下面我们来介绍一种常用的决策树模型算法,叫做Classification and Regression Tree(C&RT)。C&RT算法有两个简单的设定,首先,分支的个数\(C=2\),即二叉树(binary tree)的数据结构;然后,每个分支最后的\(g_t(x)\)(数的叶子)是一个常数。按照最小化\(E_{in}\)的目标,对于binary/multiclass classification(0/1 error)问题,看正类和负类哪个更多,\(g_t(x)\)取所占比例最多的那一类\(y_n\);对于regression(squared error)问题,\(g_t(x)\)则取所有\(y_n\)的平均值。

对于决策树的基本演算法流程,C&RT还有一些简单的设定。首先,C&RT分支个数\(C=2\),一般采用上节课介绍过的decision stump的方法进行数据切割。也就是每次在一个维度上,只对一个特征feature将数据一分为二,左子树和右子树,分别代表不同的类别。然而,怎么切割才能让数据划分得最好呢(error最小)?C&RT中使用纯净度purifying这个概念来选择最好的decision stump。purifying的核心思想就是每次切割都尽可能让左子树和右子树中同类样本占得比例最大或者\(y_n\)都很接近(regression),即错误率最小。比如说classifiacation问题中,如果左子树全是正样本,右子树全是负样本,那么它的纯净度就很大,说明该分支效果很好。

根据C&RT中purifying的思想,我们得到选择合适的分支条件\(b(x)\)的表达式如上所示。最好的decision stump重点包含两个方面:一个是刚刚介绍的分支纯净度purifying,purifying越大越好,而这里使用purifying相反的概念impurity,则impurity越小越好;另外一个是左右分支纯净度所占的权重,权重大小由该分支的数据量决定,分支包含的样本个数越多,则所占权重越大,分支包含的样本个数越少,则所占权重越小。上式中的\(D_c\) with \(h\)代表了分支\(c\)所占的权重。这里\(b(x)\)类似于error function(这也是为什么使用impurity代替purifying的原因),选择最好的decision stump,让所有分支的不纯度最小化,使\(b(x)\)越小越好。
不纯度Impurity如何用函数的形式量化?一种简单的方法就是类比于\(E_{in}\),看预测值与真实值的误差是多少。对于regression问题,它的impurity可表示为:$$impurity(D)=\frac{1}{N}\sumN_{n=1}(y_n-\bar{y})2$$ 其中,\(\overline{y}\)表示对应分支下所有\(y_n\)的均值。对于Classification 问题,它的impurity可表示为:$$impurity(D)=\frac{1}{N}\sum^N_{n=1}[y_n \neq y^*]$$ 其中,\(y^*\)表示对应分支下所占比例最大的那一类。

以上这些impurity是基于原来的regression error和classification error直接推导的。进一步来看classification的impurity functions,如果某分支条件下,其中一个分支纯度最大,那么就选择对应的decision stump,即得到的classification error为:$$1-\max_{1\leq k \leq K}\frac{\sum_{n=1}^N[y_n=k]}{N}$$ 其中\(K\)为分支个数(类别个数,返回占比最大的类别?)。
上面这个式子只考虑纯度最大的那个分支,更好的做法是将所有分支的纯度都考虑并计算在内,用基尼指数(Gini index)表示:$$1-\sumK_{k=1}(\frac{\sumN_{n=1}[y_n=k]}{N})^2$$ Gini index的优点是将所有的class在数据集中的分布状况和所占比例全都考虑了,这样让decision stump的选择更加准确。

对于决策树C&RT算法,通常来说,上面介绍的各种impurity functions中,Gini index更适合求解classification问题,而regression error更适合求解regression问题。
C&RT算法迭代终止条件有两种情况,第一种情况是当前各个分支下包含的所有样本\(y_n\)都是同类的,即不纯度impurity为0,表示该分支已经达到了最佳分类程度。第二种情况是该特征下所有的\(x_n\)相同,无法对其进行区分,表示没有decision stumps。遇到这两种情况,C&RT算法就会停止迭代。

所以,C&RT算法遇到迭代终止条件后就成为完全长成树(fully-grown tree)。它每次分支为二,是二叉树结构,采用purify来选择最佳的decision stump来划分,最终得到的叶子(\(g_t(x)\))是常数。
3. Decision Tree Heuristics in C&RT
现在我们已经知道了C&RT算法的基本流程:

可以看到C&RT算法在处理binary classification和regression问题时非常简单实用,而且,处理muti-class classification问题也十分容易。
考虑这样一个问题,有\(N\)个样本,如果我们每次只取一个样本点作为分支,那么在经过\(N-1\)次分支之后,所有的样本点都能完全分类正确。最终每片叶子上只有一个样本,有\(N\)片叶子,即必然能保证\(E_{in}=0\)。这样看似是完美的分割,但是不可避免地造成VC Dimension无限大,造成模型复杂度增加,从而出现过拟合现象。为了避免overfit,我们需要在C&RT算法中引入正则化,来控制整个模型的复杂度。
考虑到避免模型过于复杂的方法是减少叶子(\(g_t(x)\))的数量,那么可以令regularizer就为决策树中叶子的总数,记为\(\Omega(G)\)。正则化的目的是尽可能减少\(\Omega(G)\)的值。这样,regularized decision tree的形式就可以表示成:$$argmin_{all possible G}E_{in}(G)+\lambda \Omega(G)$$ 我们把这种regularized decision tree称为pruned decision tree。pruned是修剪的意思,通过regularization来修剪决策树,去掉多余的叶子,更简洁化,从而达到避免过拟合的效果。
那么如何确定修剪多少叶子,修剪哪些叶子呢?假设由C&RT算法得到一棵完全长成树(fully-grown tree),总共\(10\)片叶子。首先分别减去其中一片叶子,剩下\(9\)片,将这\(10\)种情况比较,取\(E_{in}\)最小的那个模型;然后再从\(9\)片叶子的模型中分别减去一片,剩下\(8\)片,将这\(9\)种情况比较,取\(E_{in}\)最小的那个模型。以此类推,继续修建叶子。这样,最终得到包含不同叶子的几种模型,将这几个使用regularized decision tree的error function来进行选择,确定包含几片叶子的模型误差最小,就选择该模型。另外,参数\(\lambda\)可以通过validation来确定最佳值。

我们一直讨论决策树上的叶子(features)都是numerical features,而实际应用中,决策树的特征值可能不是数字量,而是类别(categorical features)。对于numerical features,我们直接使用decision stump进行数值切割;而对于categorical features,我们仍然可以使用decision subset,对不同类别进行“左”和“右”,即是与不是(0和1)的划分。numerical features和categorical features的具体区别如下图所示:

在决策树中预测中,还会遇到一种问题,就是当某些特征缺失的时候,没有办法进行切割和分支选择。一种常用的方法就是surrogate branch,即寻找与该特征相似的替代feature。如何确定是相似的feature呢?做法是在决策树训练的时候,找出与该特征相似的feature,如果替代的feature与原feature切割的方式和结果是类似的,那么就表明二者是相似的,就把该替代的feature也存储下来。当预测时遇到原feature缺失的情况,就用替代feature进行分支判断和选择。

4. Decision Tree in Action
最后我们来举个例子看看C&RT算法究竟是如何进行计算的。例如下图二维平面上分布着许多正负样本,我们使用C&RT算法来对其进行决策树的分类。
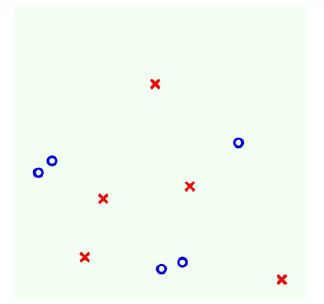
第一步:
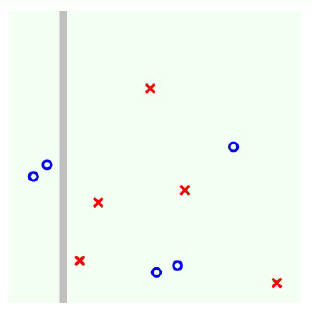
第二步:

第三步:
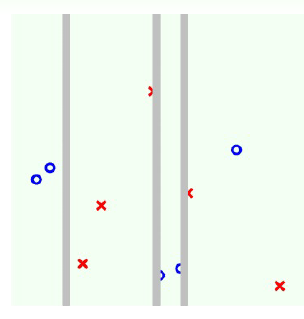
第四步:

在进行第四步切割之后,我们发现每个分支都已经非常纯净了,没有办法继续往下切割。此时表明已经满足了迭代终止条件,这时候就可以回传base hypothesis,构成sub tree,然后每个sub tree再往上整合形成tree,最后形成我们需要的完全决策树。如果将边界添加上去,可得到下图:
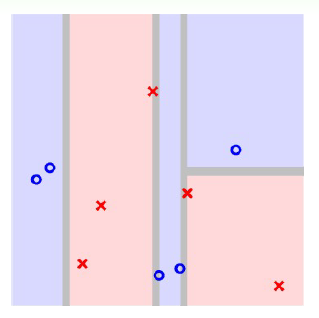
得到C&RT算法的切割方式之后,我们与AdaBoost-Stump算法进行比较:
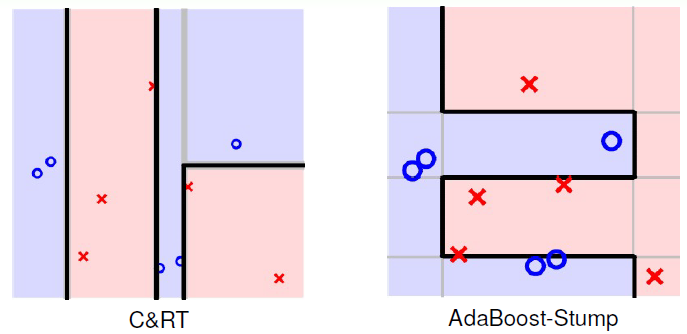
我们之前就介绍过,AdaBoost-Stump算法的切割线是横跨整个平面的;而C&RT算法的切割线是基于某个条件的,所以一般不会横跨整个平面。比较起来,虽然C&RT和AdaBoost-Stump都采用decision stump方式进行切割,但是二者在细节上还是有所区别。
再看一个数据集分布比较复杂的例子,C&RT和AdaBoost-Stump的切割方式对比效果如下图所示:
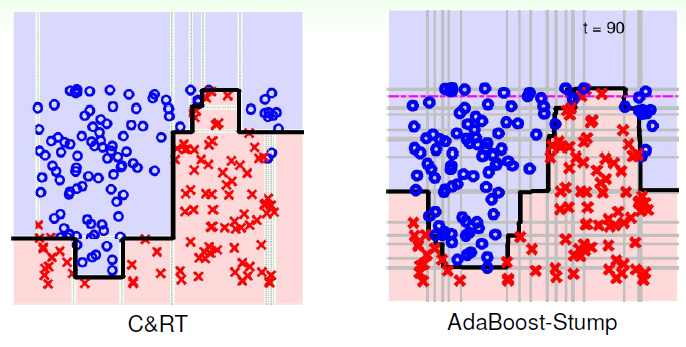
通常来说,由于C&RT是基于条件进行切割的,所以C&RT比AdaBoost-Stump分类切割更有效率。总结一下,C&RT决策树有以下特点:

5. 总结
本节课主要介绍了Decision Tree。首先将decision tree hypothesis对应到不同分支下的矩\(g_t(x)\)。然后再介绍决策树算法是如何通过递归的形式建立起来。接着详细研究了决策树C&RT算法对应的数学模型和算法架构流程。最后通过一个实际的例子来演示决策树C&RT算法是如何一步一步进行分类的。




