机器学习基石5-训练与测试
注:
文章中所有的图片均来自台湾大学林轩田《机器学习基石》课程。
笔记原作者:红色石头
微信公众号:AI有道
上节课主要介绍了机器学习的可行性。首先,由NFL定理可知,机器学习貌似是不可行的。但是,随后引入了统计学知识,如果样本数据足够大,且hypothesis个数有限,那么机器学习一般就是可行的。本节课将讨论机器学习的核心问题,严格证明为什么机器可以学习。从上节课最后的问题出发,即当hypothesis的个数是无限多的时候,机器学习的可行性是否仍然成立?
一、Recap and Preview
先来看一下基于统计学的机器学习流程图:
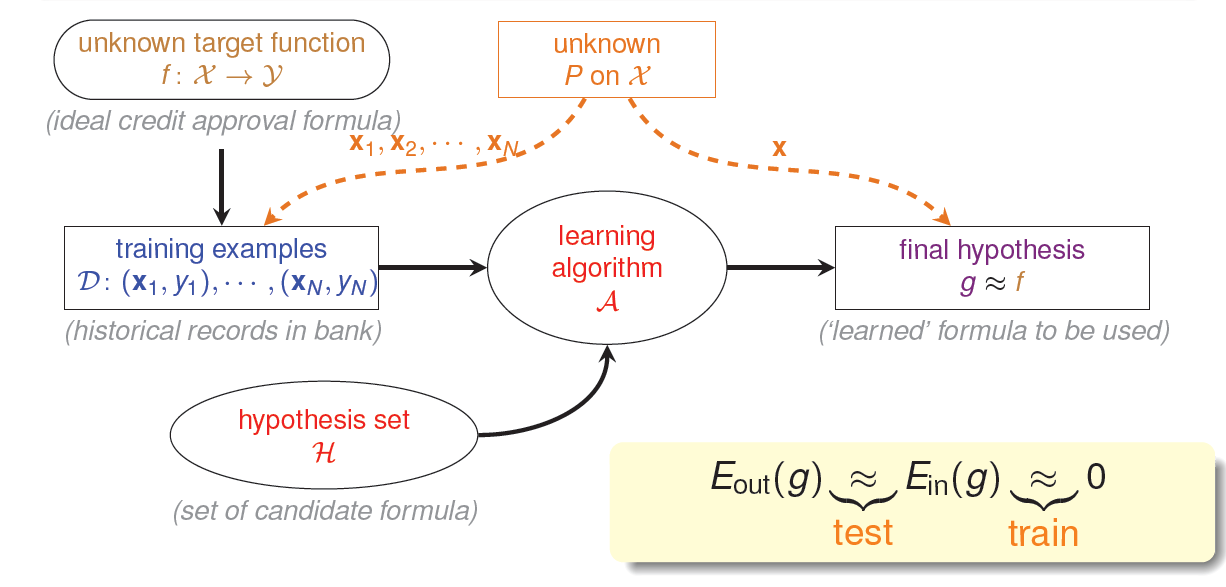
该流程图中,训练样本D和最终测试\(h\)的样本都是来自同一个数据分布,这是机器能够学习的前提。另外,训练样本D应该足够大,且hypothesis set的个数是有限的,这样根据霍夫丁不等式,才不会出现Bad Data,保证\(E_{in}\approx E_{out}\),即有很好的泛化能力。同时,通过训练,得到使\(E_{in}\)最小的\(h\),作为模型最终的\(g\),\(g\)接近于目标函数。
总结一下前四节课的内容:第一节课,介绍了机器学习的定义,目标是找出最好的\(g\),使\(g\approx f\),保证\(E_{out}\approx 0\) ; 第二节课,介绍了如何让\(E_{in}\approx 0\),可以使用PLA、pocket等演算法来实现;;第三节课,介绍了机器学习的分类,我们的训练样本是批量数据(batch),处理监督式(supervised)二元分类(binary classification)问题;第四节课,介绍了机器学习的可行性,通过统计学知识,把\(E_{in}\)与\(E_{out}\)联系起来,证明了在一些条件假设下,有\(E_{in}\approx E_{out}\)成立。

总结下来,机器学习的主要目标被分成了两个核心问题:
-
\(E_{in}(g)\approx E_{out}(g)\)
-
\(E_{in}(g)\) 足够小
上节课介绍的机器学习可行的一个条件是hypothesis set的个数\(M\)是有限的,那\(M\)跟上面这两个核心问题有什么联系呢?
先来看一下,当\(M\)很小的时候,由上节课介绍的霍夫丁不等式,得到\(E_{in}(g)\approx E_{out}(g)\),即能保证第一个核心问题成立。但\(M\)很小时,演算法A可以选择的hypothesis有限,不一定能找到使\(E_{in}(g)\)足够小的hypothesis,即不能保证第二个核心问题成立。当\(M\)很大的时候,同样由霍夫丁不等式, \(E_{in}(g)\)与\(E_{out}(g)\)的差距可能比较大,第一个核心问题可能不成立。而\(M\)很大,使的演算法A的可以选择的hypothesis就很多,很有可能找到一个hypothesis,使\(E_{in}(g)\)足够小,第二个核心问题可能成立。

从上面的分析来看,\(M\)的选择直接影响机器学习两个核心问题是否满足,\(M\)不能太大也不能太小。那么如果\(M\)无限大的时候,是否机器就不可以学习了呢?例如PLA算法中直线是无数条的,但是PLA能够很好地进行机器学习,这又是为什么呢?如果我们能将无限大的\(M\)限定在一个有限的\(m_{H}\)内,问题似乎就解决了。
二、Effective Number of Line
先看一下上节课推导的霍夫丁不等式:$$P[|E_{in}(g)-E_{out}(g)|>\epsilon]\leq 2Mexp(-2\epsilon^2 N)$$
其中,\(M\)表示hypothesis的个数。每个hypothesis下的BAD events 级联的形式满足下列不等式:
当\(M=\infty\)时,上面不等式式右边值将会很大,似乎说明BAD events很大, \(E_{in}(g)\)与\(E_{out}(g)\)也并不接近。但是BAD events 级联的形式实际上扩大了上界,union bound过大。这种做法假设各个hypothesis之间没有交集,这是最坏的情况,可是实际上往往不是如此,很多情况下都是有交集的,也就是说\(M\)实际上没那么大,如下图所示:
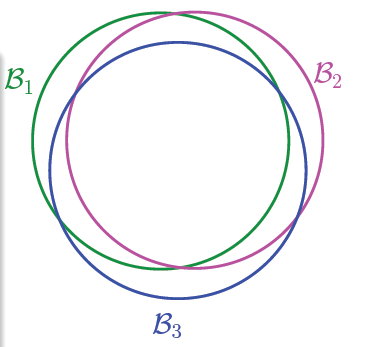
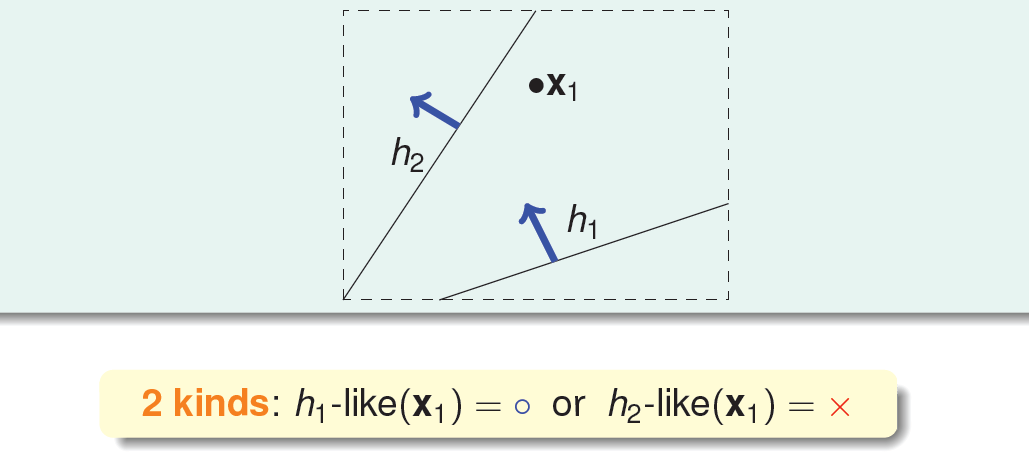
也就是说union bound被估计过高了(over estimating)。所以,我们的目的是找出不同BAD events之间的重叠部分,也就是将无数个hypothesis分成有限个类别。如何将无数个hypothesis分成有限类呢?先来看这样一个例子,假如平面上用直线将点分开,也就跟PLA一样。如果平面上只有一个点\(X_1\),那么直线的种类有两种:一种将\(X_1\)划为\(+1\),一种将\(X_1\)划为\(-1\):
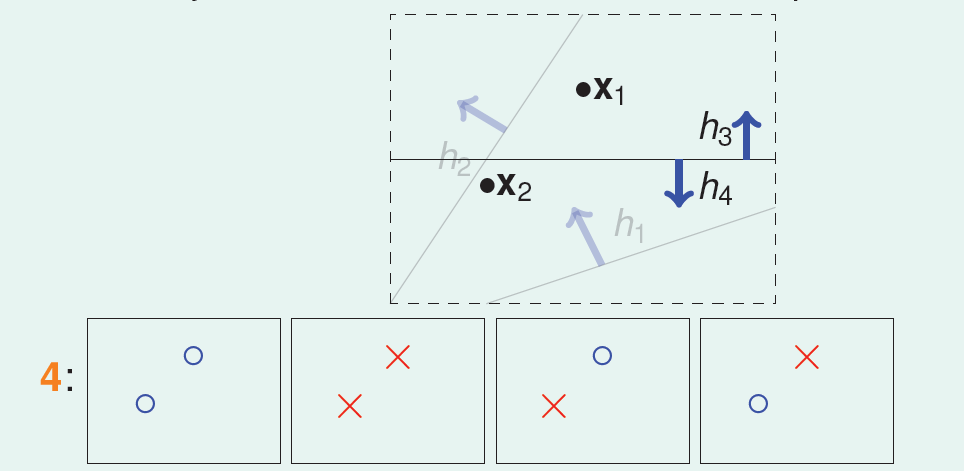
如果平面上有两个点\(X_1\)、\(X_2\),那么直线的种类共4种:\(X_1\)、\(X_2\)都为\(+1\),\(X_1\)、\(X_2\)都
为\(-1\),\(X_1\)为\(+1\)且\(X_2\)为\(-1\),\(X_1\)为\(-1\)且\(X_2\)为\(+1\):
如果平面上有三个点\(X_1\)、\(X_2\)、\(X_3\),那么直线的种类共8种:
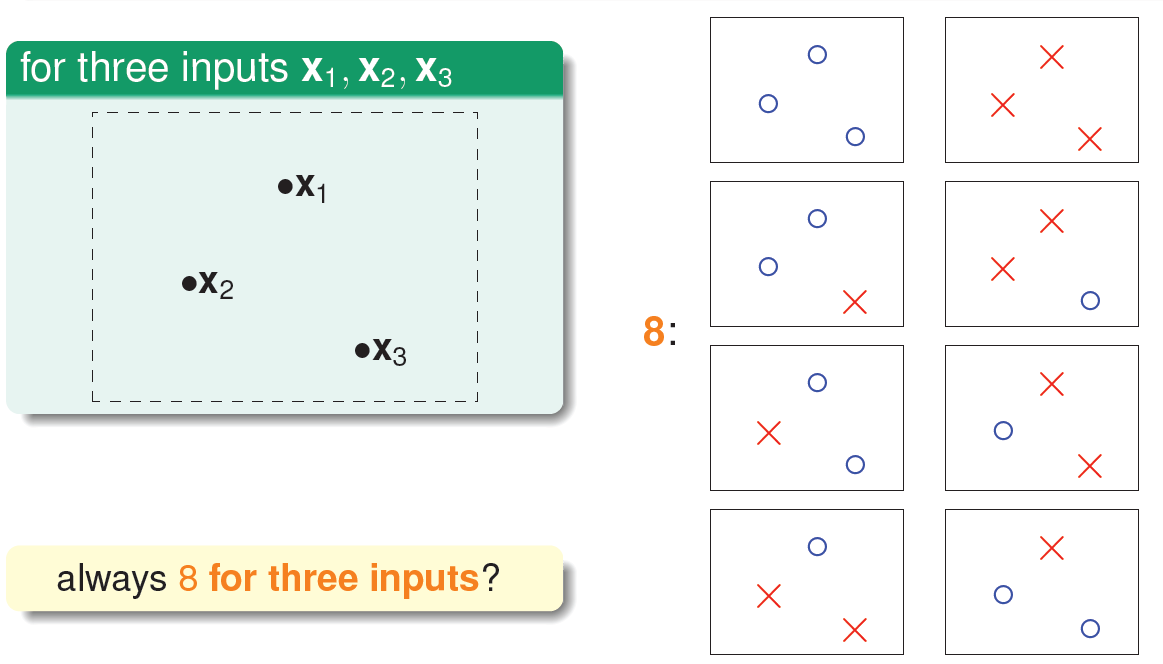
但是在三个点的情况下,也会出现不能用一条直线划分的情况:
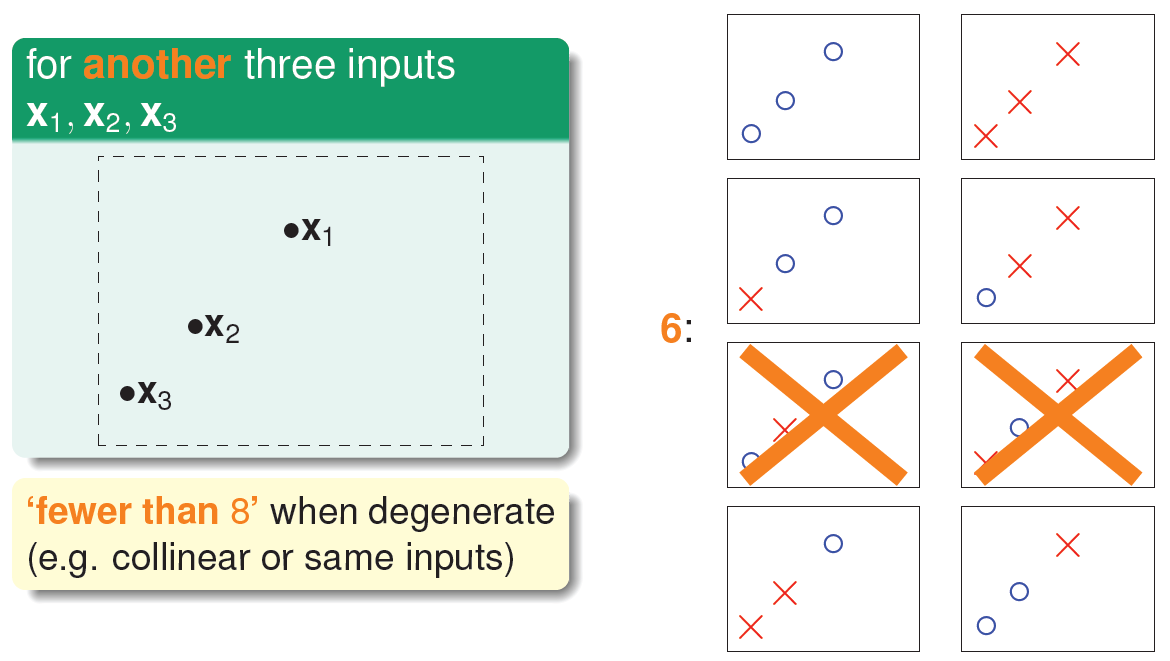
也就是说,对于平面上三个点,不能保证所有的8个类别都能被一条直线划分。那如果是四个点\(X_1\)、\(X_2\)、\(X_3\)、\(X_4\),我们发现,平面上找不到一条直线能将四个点组成的16个类别完全分开,最多只能分开其中的14类,即直线最多只有14种:
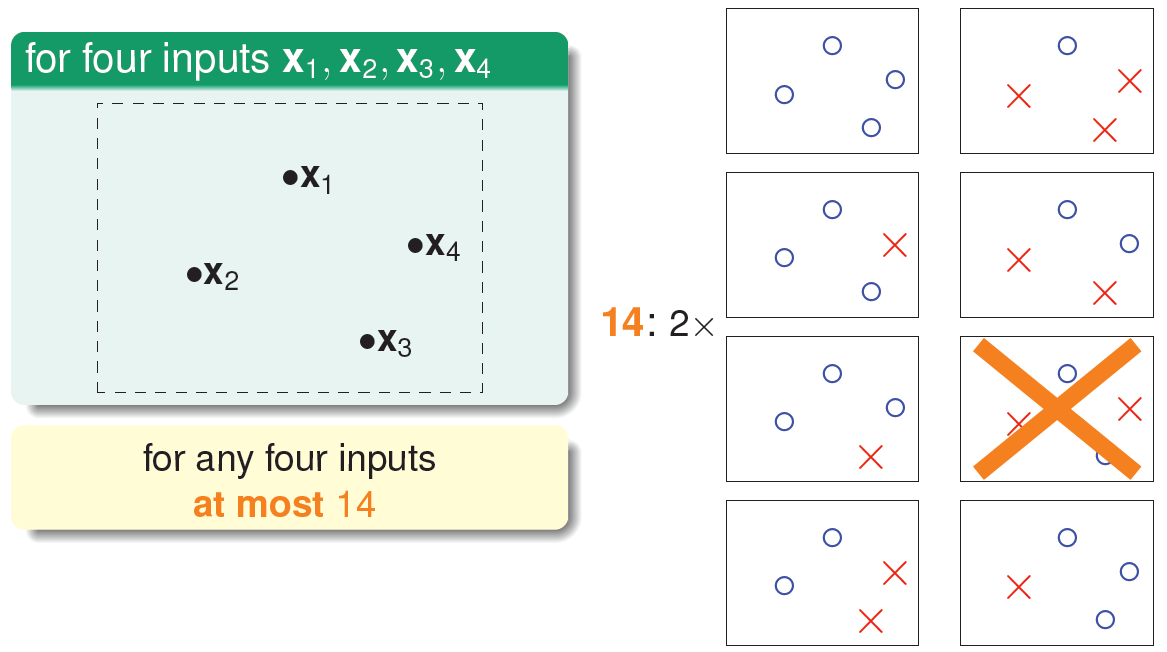
经过分析,我们得到平面上线的种类是有限的,1个点最多有2种线,2个点最多有4种线,3个点最多有8种线,4个点最多有14(\(<2^4\) )种线等等。我们发现,有效直线的数量总是满足\(\leq 2^N\),其中,\(N\)是点的个数。所以,如果我们可以用effective(\(N\))代替\(M\),霍夫丁不等式可以写成:
已知\(\text{effective}(N)<2^N\),如果能够保证\(\text{effective}(N)\ll 2^N\),即不等式右边接近于零,那么即使\(M\)无限大,直线的种类也很有限,机器学习也是可能的。

三、Effective Number of Hypotheses
接下来先介绍一个新名词:二分类(dichotomy)。dichotomy就是将空间中的点(例如二维平面)用一条直线分成正类(蓝色o)和负类(红色x)。令H是将平面上的点用直线分开的所有hypothesis h的集合,dichotomy H与hypotheses H的关系是:hypotheses H是平面上所有直线的集合,个数可能是无限个,而dichotomy H是平面上能将点完全用直线分开的直线种类,它的上界是\(2^N\)。接下来,我们要做的就是尝试用dichotomy代替\(M\)。

再介绍一个新的名词:成长函数(growth function),记为\(m_H(N)\)。成长函数的定义是:对于由\(N\)个点组成的不同集合中,某集合对应的dichotomy最大,那么这个dichotomy值就是\(m_H(N)\),它的上界是\(2^N\):
成长函数其实就是我们之前讲的effective lines的数量最大值。根据成长函数的定义,二维平面上, 随\(N\)的变化关系是:

接下来,我们讨论如何计算成长函数。先看一个简单情况,一维的Positive Rays:
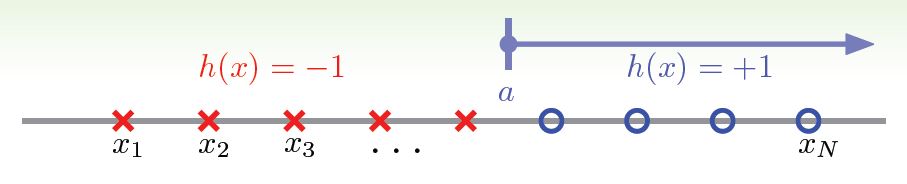
若有\(N\)个点,则整个区域可分为\(N+1\)段,很容易得到其成长函数\(m_H(N)=N+1\)。
注意当\(N\)很大时,\((N+1)\ll 2^N\) ,这是我们希望看到的。
另一种情况是一维的Positive Intervals:

它的成长函数可以由下面推导得出:

在这种情况下,当\(N\)很大的时候, \(m_H(N)=\frac{1}{2}N^2+\frac{1}{2}N+1 \ll 2^N\)。
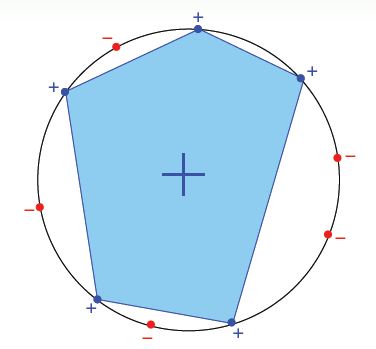
再来看这个例子,假设在二维空间里,如果hypothesis是凸多边形或类圆构成的封闭曲线,如下图所示,左边是convex的,右边不是convex的。那么,它的成长函数是多少呢?

当数据集D按照如下的凸分布时,我们很容易计算得到它的成长函数\(m_H=2^N\)。这种情况下,\(N\)个点所有可能的分类情况都能够被hypotheses set覆盖,我们把这种情形称为shattered。也就是说,如果能够找到一个数据分布集,hypotheses set对\(N\)个输入所有的分类情况都做得到,那么它的成长函数就是\(2^N\)。
四、Break Point
上一小节,我们介绍了四种不同的成长函数,分别是:

其中,positive rays和positive intervals的成长函数都是polynomial的,如果用代替\(M\)的话,这两种情况是比较好的。而convex sets的成长函数是exponential的,即等于\(M\),并不能保证机器学习的可行性。那么,对于2D perceptrons,它的成长函数究竟是polynomial的还是exponential的呢?
对于2D perceptrons,我们之前分析了3个点,可以做出8种所有的dichotomy,而4个点,就无法做出所有16种dichotomy了。所以,我们就把4称为2D perceptrons的break point(5、6、7等都是break point)。令有\(N\)个点,如果\(N\)大于等于break point时,它的成长函数一定小于2的\(N\)次方。
根据break point的定义,我们知道满足\(m_H(k)\leq 2^k\)的\(k\)的最小值就是break point。对于我们之前介绍的四种成长函数,他们的break point分别是:

通过观察,我们猜测成长函数可能与break point存在某种关系:对于convex sets,没有break point,它的成长函数是2的N次方;对于positive rays,break point \(k=2\),它的成长函数是\(O(N)\);对于positive intervals,break point \(k=3\),它的成长函数是\(O(N^2)\)。则根据这种推论,我们猜测2D perceptrons,它的成长函数是\(m_H(N)=O(N^{k-1})\)。如果成立,那么就可以用\(m_H\)代替\(M\),就满足了机器能够学习的条件。关于上述猜测的证明,下节课再详细介绍。
五、总结
本节课更深入地探讨了机器学习的可行性。我们把机器学习拆分为两个核心问题:\(E_{in}(g)\approx E_{out}(g)\) 和 \(E_{in}(g)\approx 0\)。对于第一个问题,我们探讨了\(N\)个点到底可以划分为多少种,也就是成长函数\(m_H(N)\)。并引入了break point的概念,给出了break point的计算方法。下节课,我们将详细论证对于2D perceptrons,它的成长函数与break point是否存在多项式的关系,如果是这样,那么机器学习就是可行的。




