机器学习基石2-Learning to Answer Yes-No
注:
文章中所有的图片均来自台湾大学林轩田《机器学习基石》课程。
笔记原作者:红色石头
微信公众号:AI有道
上节课,简述了机器学习的定义及其重要性,并用流程图的形式介绍了机器学习的整个过程:根据模型\(\mathcal{H}\),使用演算法\(\mathcal{A}\),在训练样本\(\mathcal{D}\)上进行训练,得到最好的\(h\),其对应的\(g\)就是我们最后需要的机器学习的模型函数,一般\(g\)接近于目标函数\(f\)。本节课将继续深入探讨机器学习问题,介绍感知机Perceptron模型,并推导课程的第一个机器学习算法:Perceptron Learning Algorithm(PLA)。
一、Perceptron Hypothesis Set
引入这样一个例子:某银行要根据用户的年龄、性别、年收入等情况来判断是否给该用户发信用卡。现在有训练样本\(\mathcal{D}\),即之前用户的信息和是否发了信用卡。这是一个典型的机器学习问题,我们要根据\(\mathcal{D}\),通过\(\mathcal{A}\),在\(\mathcal{H}\)中选择最好的\(h\),得到\(g\),接近目标函数\(f\),也就是根据先验知识建立是否给用户发信用卡的模型。银行用这个模型对以后用户进行判断:发信用卡(+1),不发信用卡(-1)。
在这个机器学习的整个流程中,有一个部分非常重要:就是模型选择,即Hypothesis Set。选择什么样的模型,很大程度上会影响机器学习的效果和表现。下面介绍一个简单常用的Hypothesis Set:感知机(Perceptron)。
还是刚才银行是否给用户发信用卡的例子,我们把用户的个人信息作为特征向量\(x\),令总共有\(d\)个特征,每个特征赋予不同的权重\(w\),表示该特征对输出(是否发信用卡)的影响有多大。拿所有特征的加权和的值与一个设定的阈值threshold进行比较:大于这个阈值,输出为\(+1\),即发信用卡;小于这个阈值,输出为\(-1\),即不发信用卡。感知机模型,就是当特征加权和与阈值的差大于或等于\(0\),则输出\(h(x)=1\);当特征加权和与阈值的差小于\(0\),则输出\(h(x)=1\),而我们的目的就是计算出所有权值\(w\)和阈值threshold。
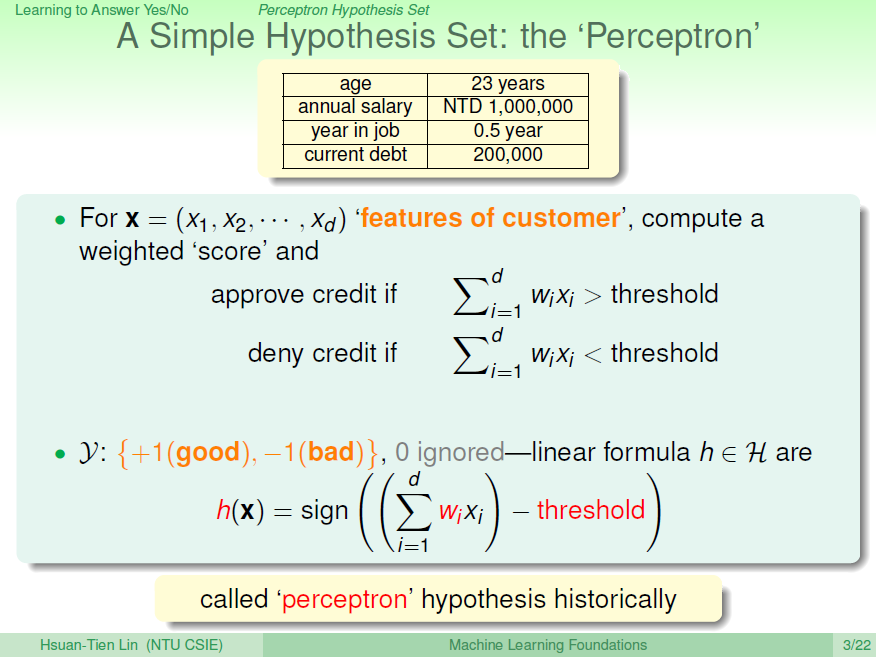
为了计算方便,通常我们将阈值threshold当做\(w_0\),引入一个\(x_0=1\)的量与\(w_0\)相乘,这样就把threshold也转变成了权值,简化了计算。\(h(x)\)的表达式做如下变换:

为了更清晰地说明感知机模型,我们假设Perceptrons在二维平面上,即\(h(x)=sign(w_0+w_1x_1+w_2x_2)\)。其中,\(w_0+w_1x_1+w_2x_2=0\) 是平面上一条分类直线,直线一侧是正类\((+1)\),直线另一侧是负类\((-1)\)。权重\(w\)不同,对
应于平面上不同的直线。
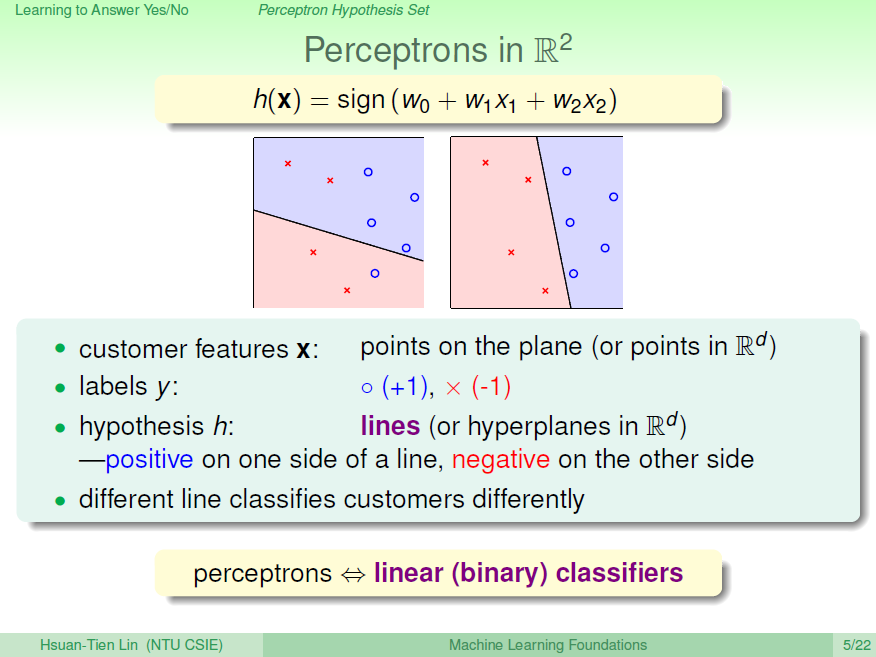
那么,我们所说的Perceptron,在这个模型上就是一条直线,称之为linear(binary) classifiers。注意一下,感知器线性分类不限定在二维空间中,在3D中,线性分类用平面表示,在更高维度中,线性分类用超平面表示,即只要是形如的线性模型就都属于linear(binary) classifiers。同时,需要注意的是,这里所说的linear(binary) classifiers是用简单的感知器模型建立的,线性分类问题还可以使用logistic regression来解决,后面将会介绍。
二、Perceptron Learning Algorithm (PLA)
根据上一部分的介绍,我们已经知道了hypothesis set由许多条直线构成。接下来,我们的目的就是如何设计一个演算法\(\mathcal{A}\),来选择一个最好的直线,能将平面上所有的正类和负类完全分开,也就是找到最好的\(g\),使\(g\approx f\)。
如何找到这样一条最好的直线呢?我们可以使用逐点修正的思想,首先在平面上随意取一条直线,看看哪些点分类错误。然后开始对第一个错误点就行修正,即变换直线的位置,使这个错误点变成分类正确的点。接着,再对第二个、第三个等所有的错误分类点就行直线纠正,直到所有的点都完全分类正确了,就得到了最好的直线。这种“逐步修正”,就是PLA思想所在。

下面介绍一下PLA是怎么做的。首先随机选择一条直线进行分类。然后找到第一个分类错误的点,如果这个点表示正类,被误分为负类,即\(w^T_tx_{n(t)}<0\),那表示\(w\)和\(x\)夹角大于90度,其中\(w\)是直线的法向量。所以,\(x\)被误分在直线的下侧(相对于法向量,法向量的方向即为正类所在的一侧),修正的方法就是使\(w\)和\(x\)夹角小于90度。通常做法是\(w\leftarrow w+yx\),\(y=1\), 如图右上角所示,一次或多次更新后的\(w+yx\)与\(x\)夹角小于90度,能保证\(x\)位于直线的上侧,则对误分为负类的错误点完成了直线修正。
同理,如果是误分为正类的点,即\(w^T_tx_{n(t)}>0\),那表示\(w\)和\(x\)夹角小于90度,其中\(w\)是直线的法向量。所以,\(x\)被误分在直线的上侧,修正的方法就是使\(w\)和\(x\)夹角大于90度。通常做法是\(w\leftarrow w+yx\),\(y=-1\),如图右下角所示,一次或多次更新后的\(w\)与\(x\)夹角大于90度,能保证\(x\)位于直线的下侧,则对误分为正类的错误点也完成了直线修正。
按照这种思想,遇到个错误点就进行修正,不断迭代。要注意一点:每次修正直线,可能使之前分类正确的点变成错误点,这是可能发生的。但是没关系,不断迭代,不断修正,最终会将所有点完全正确分类(PLA前提是线性可分的)。这种做法的思想是“知错能改”,有句话形容它:“A fault confessed is half redressed.”
实际操作中,可以一个点一个点地遍历,发现分类错误的点就进行修正,直到所有点全部分类正确。这种被称为Cyclic PLA。

下面用图解的形式来介绍PLA的修正过程:
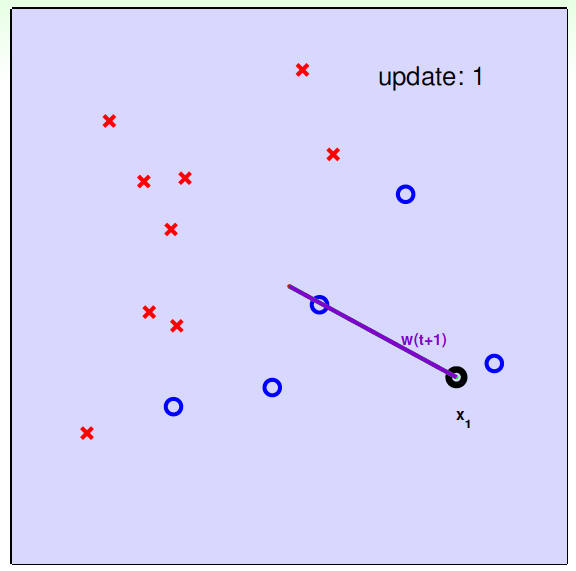
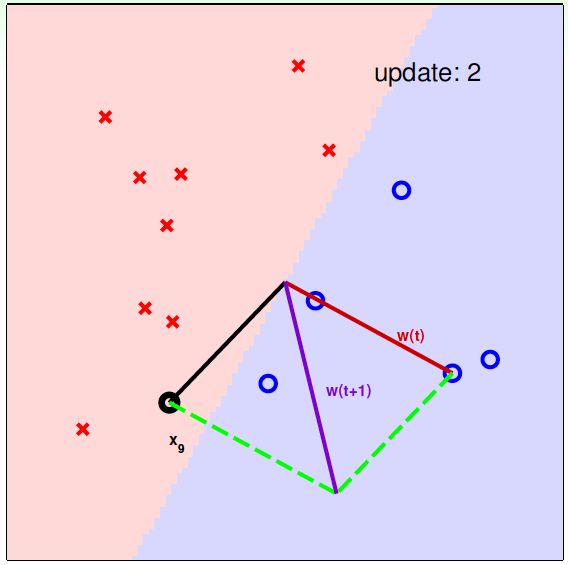
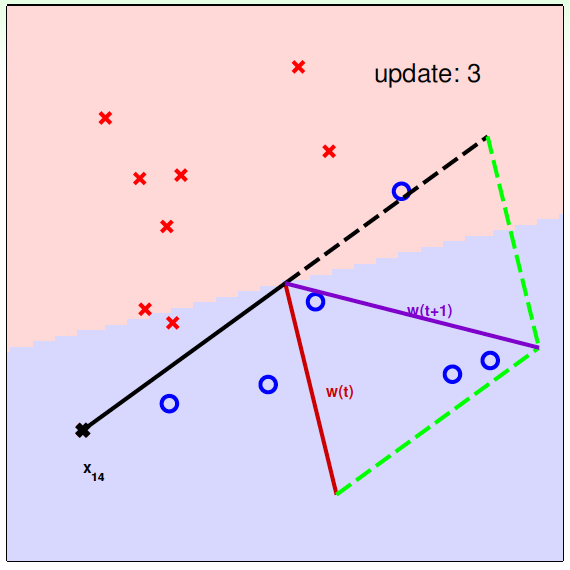
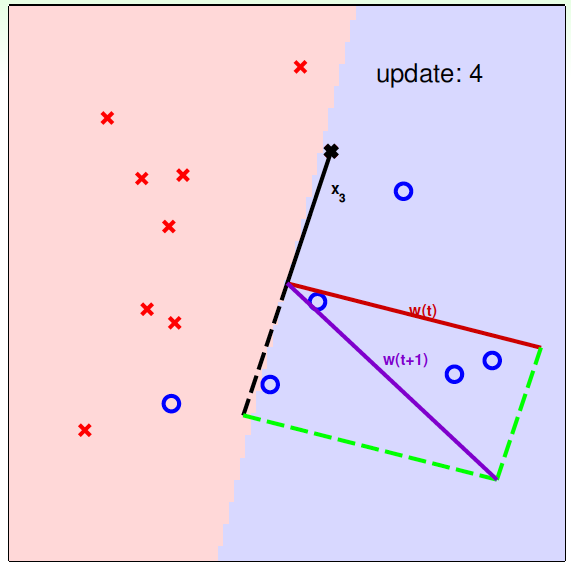
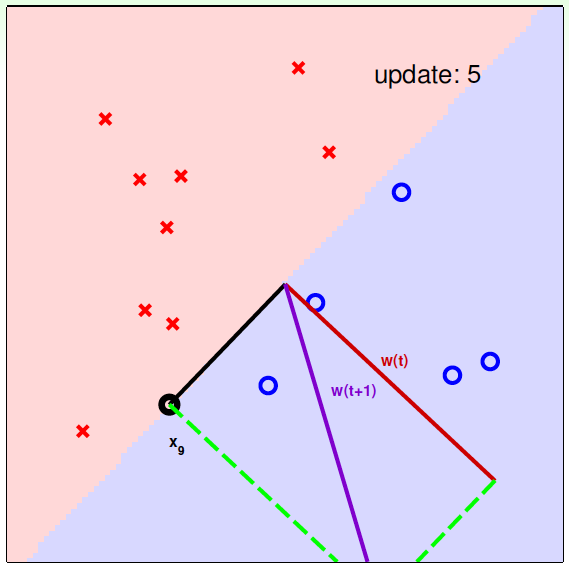
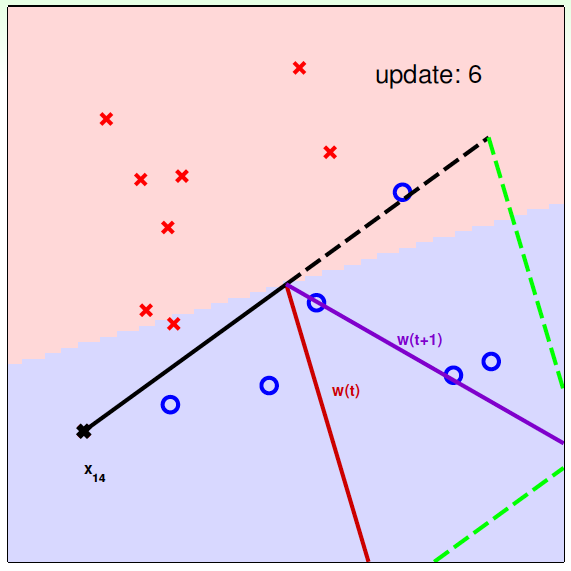
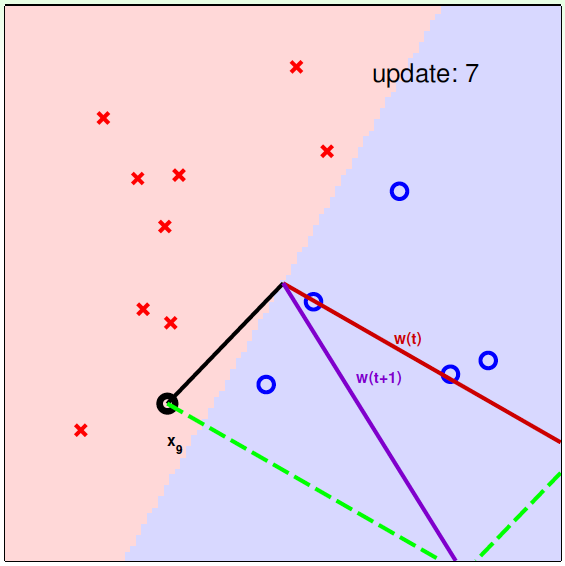
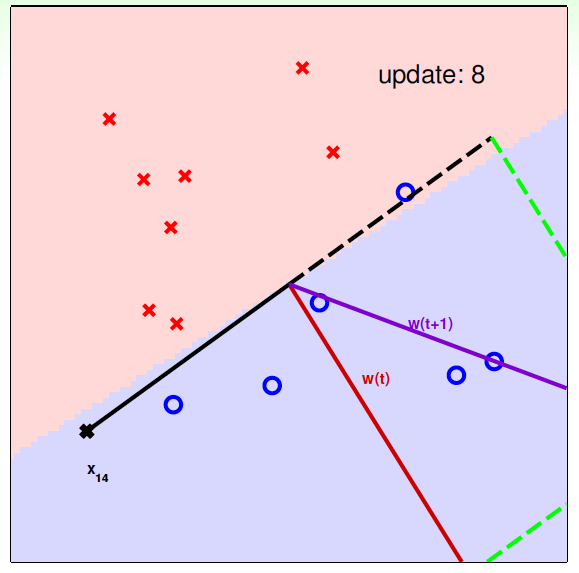
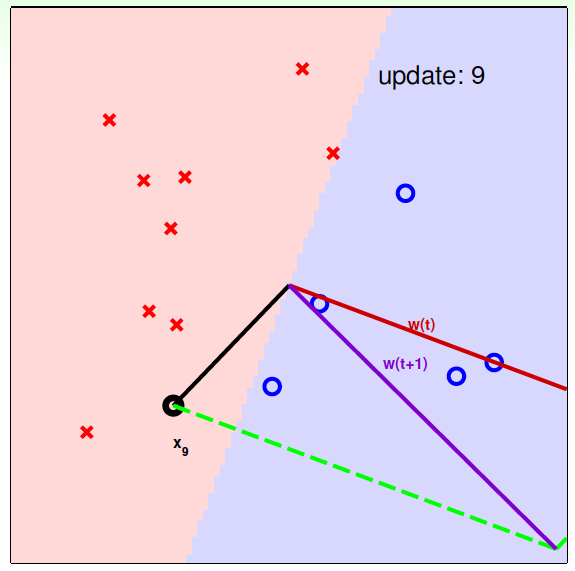
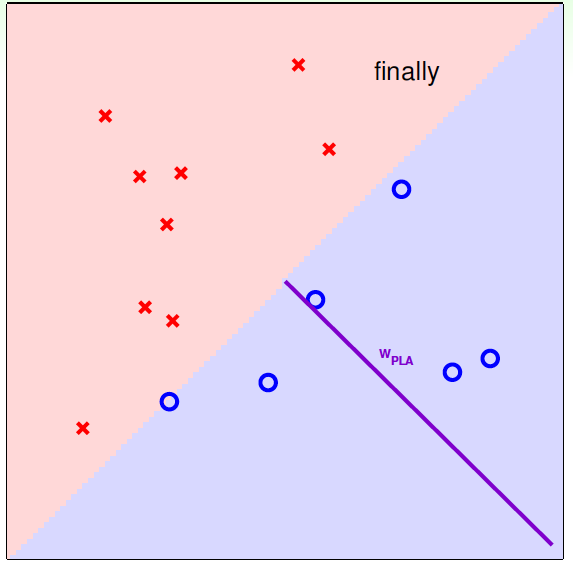
对PLA,我们需要考虑以下两个问题:
- PLA迭代一定会停下来吗?如果线性不可分怎么办?
- PLA停下来的时候,是否能保证\(f\approx g\)?如果没有停下来,是否有\(f\approx g\)?
三、Guarantee of PLA
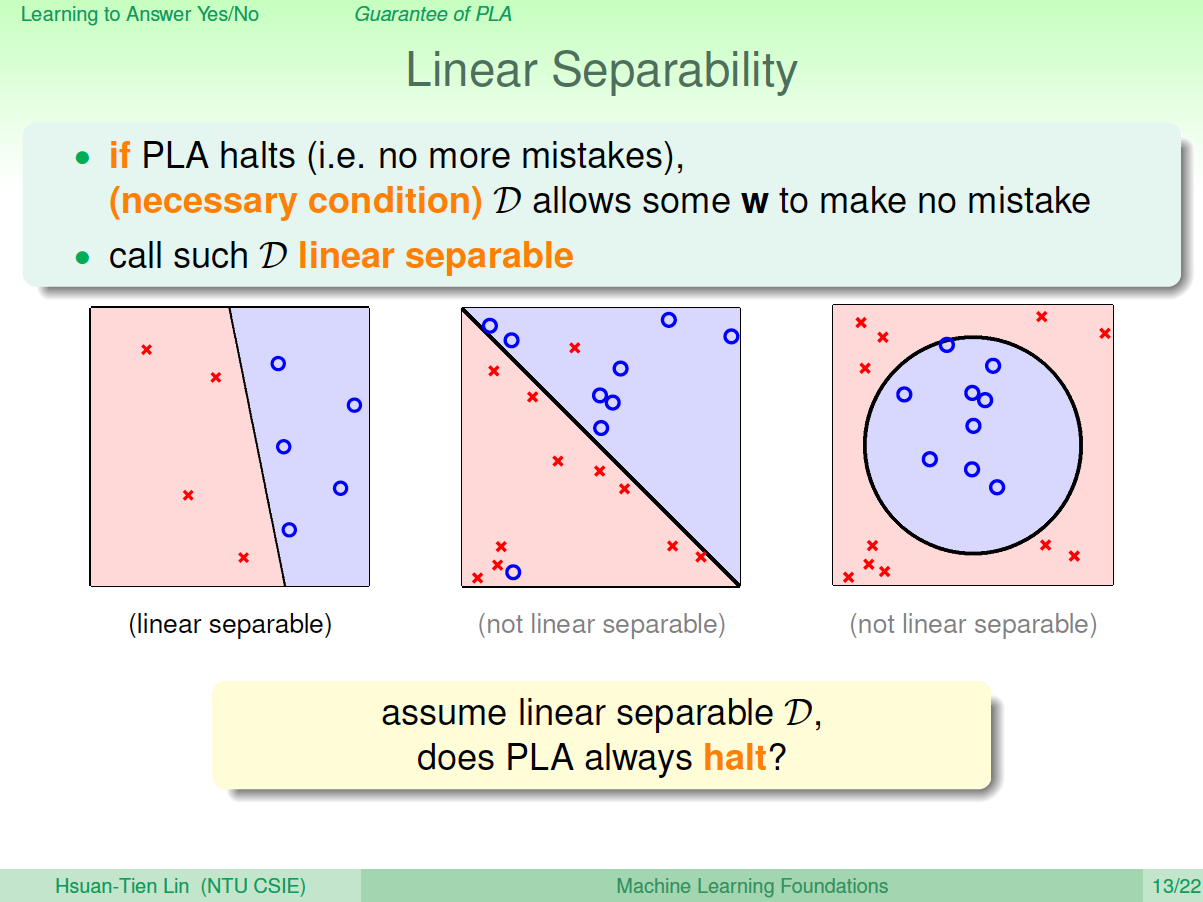
PLA什么时候会停下来呢?根据PLA的定义,当找到一条直线,能将所有平面上的点都分类正确,那么PLA就停止了。要达到这个终止条件,就必须保证D是线性可分(linear separable)。如果是非线性可分的,那么,PLA就不会停止。
对于线性可分的情况,如果有这样一条直线,能够将正类和负类完全分开,令这时候的目标权重为\(w_f\),则对每个点,必然满足\(y_n=sign(w^T_fx_n)\),即对任一点:$$y_{n(t)}w^T_fx_{n(t)}\geq min_{n}y_nw^T_fx_n>0$$ PLA会对每次错误的点进行修正,更新权重\(w_{t+1}\)的值,如果\(w_{t+1}\)与\(w_f\)越来越接近,数学运算上就是内积越大,那表示\(w_{t+1}\)是在接近目标权重\(w_f\),证明PLA是有学习效果的。所以,我们来计算\(w_{t+1}\)与\(w_f\)的内积:

从推导可以看出, \(w_{t+1}\)与\(w_f\)的内积跟\(w_t\)与\(w_f\)的内积相比更大了。似乎说明了\(w_{t+1}\)更接近\(w_f\),但是内积更大,可能是向量长度更大了,不一定是向量间角度更小。所以,下一步,我们还需要证明\(w_{t+1}\)与\(w_t\)向量长度的关系:

\(w_t\)只会在分类错误的情况下更新,最终得到的\(\|w_{t+1}\|^2\)相比\(\|w_{t}\|^2\)的增量值不超过\(max\|x_n\|^2\)。也就是说, \(w_t\)的增长被限制了, \(w_{t+1}\)与\(w_t\)向量长度不会差别太大!
如果令初始权值\(w_0=0\),那么经过T次错误修正后,有如下结论:




