傅里叶分析讲解三

引用：https://www.jianshu.com/p/f5a89d76eb28

上一篇中简单介绍了什么是傅里叶级数，最后得到了在周期为2\pi的傅里叶级数的系数解，那么如何得到任意周期的傅里叶级数呢？

我们先看在周期为2\pi的函数傅里叶级数表达:
f(x)= \frac{a_0}{2}+\sum_{n=1}^\infty (a_ncos(nx) +b_nsin(nx) )
其对应的解为：
a_0=\frac{1}{\pi }\int_{-\pi}^\pi f(x)dx
a_n=\frac{1}{\pi }\int_{-\pi}^\pi f(x)cos(nx)dx
b_n=\frac{1}{\pi }\int_{-\pi}^\pi f(x)fin(nx)dx
如何将其变为任意周期的函数呢？

其实这里只需要简单的换元操作即可。
举个栗子:
f(x)=\sin(x)其周期为2\pi,f(x)=f(x+2\pi)。我们令 x=2t,则f(x)=f(2t)=f(2t+2\pi)=f(2(t+\pi)),整理下:
f(2(t))=f(2(t+\pi))
所以在对于t来说就变换成了周期为\pi的函数。
so对于周期为2L（方便计算）的函数f(t) 只需令 x=\frac{\pi}{L}t带入原周期为2\pi的函数即可：
f(t)= \frac{a_0}{2}+\sum_{n=1}^\infty (a_ncos(\frac{\pi nt}{L}) +b_nsin(\frac{\pi nt}{L}) )
同样的可以得到：
\cos(x)=\cos(\frac{\pi t}{L})
\sin(x)=\sin(\frac{\pi t}{L}) )
\int_{-\pi}^\pi dx=\int_{-L}^L d\frac{\pi t}{L}
最后我们得到:
a_0=\frac{1}{L }\int_{-L}^L f(t)dt
a_n=\frac{1}{L }\int_{-L}^L f(t)cos(\frac{\pi nt}{L})dt
b_n=\frac{1}{L }\int_{-L}^L f(t)sin(\frac{\pi nt}{L})dt

过程很简单，我就省略了，毕竟人生苦短。

2 傅里叶级数的复数形式

我们在写一下傅里叶级数的公式：
f(t)= \frac{a_0}{2}+\sum_{n=1}^\infty (a_ncos(n \omega t) +b_nsin(n \omega t) ) \\ \omega=\frac{2\pi }{T}
其中T代表函数的周期，也就是上面的2L，对应的解就是:

a_0=\frac{2}{T }\int_{0}^T f(t)dt
a_n=\frac{2}{T }\int_{0}^T f(t)cos(n \omega t)dt
b_n=\frac{2}{T }\int_{0}^T f(t)sin(n \omega t)dt

想要得到傅里叶级数的复数形式，需要先了解下欧拉公式。
关于欧拉公式，网上有很多的博客，这里就不细说了，只是简单说下欧拉公式的本质。
我们先看下公式：
e^{i\theta}=cos(\theta)+isin(\theta)

e^{i\theta}可以看作是复平面上的一个向量，其到实轴的投影是cos(\theta)，到虚轴的投影是isin(\theta)，其中\theta便是向量与实轴的夹角。

 
image.png

 

而欧拉公式的直观理解就是在复平面上做圆周运动

 

 
欧拉公式.gif

随着\theta变化，e^{i\theta}就变成圆周运动了。而前面的系数a则是圆的半径，当a=1的时候就是在单位圆上做圆周运动。

而且通过欧拉公式，我们可以得到三角函数的复数形式：
\cos(\theta)=\frac{1}{2}(e^{i \theta}+e^{-i \theta}) \\ \sin(\theta)=-\frac{1}{2}i(e^{i \theta}-e^{-i \theta} )

将上面的复变三角函数替换傅里叶级数中的三角函数得到:
f(t)= \frac{a_0}{2}+\sum_{n=1}^\infty (a_n\frac{1}{2}(e^{i n \omega t}+e^{-i n \omega t}) -b_n\frac{i}{2}(e^{i n \omega t}-e^{-i n \omega t})) \\ =\frac{a_0}{2}+\sum_{n=1}^\infty ((a_n\frac{1}{2}e^{i n \omega t}+a_n\frac{1}{2}e^{-i n \omega t}) -(b_n\frac{i}{2}e^{i n \omega t}- b_n\frac{i}{2}e^{-i n \omega t})) \\ =\frac{a_0}{2}+\sum_{n=1}^\infty ((\frac{a_n-b_ni}{2}e^{i n \omega t}+\frac{a_n+b_ni}{2}e^{-i n \omega t}) ) \\ =\sum_{n=0}^0\frac{a_0}{2} e^{in\omega t}+\sum_{n=1}^\infty (\frac{a_n-b_ni}{2}e^{i n \omega t})+\sum_{n=1}^\infty(\frac{a_n+b_ni}{2}e^{-i n \omega t} )
我们令\sum_{n=1}^\infty(\frac{a_n+b_ni}{2}e^{-i n \omega t} )中的n为-n
则得到：
f(t)=\sum_{n=0}^0\frac{a_0}{2} e^{in\omega t}+\sum_{n=1}^\infty (\frac{a_n-b_n}{2}e^{i n \omega t})+\sum_{n=-\infty}^{-1}(\frac{a_{-n}+b_{-n}i}{2}e^{-i -n \omega t} )
所以可以看到n的范围变成了-\infty 到 \infty，并且每一项都有e^{i n \omega t}，于是我们可以得到一个漂亮的形式：
f(t)=\sum_{n=-\infty}^{\infty}C_n e^{in\omega t}

其中C_n分为3中情况：
n=0 \quad\quad C_n=\frac{a_0}{2} \\ n=1,2,3... \quad C_n=\frac{a_n-b_ni}{2}\\ n=-1,-2,-3... \quad C_n=\frac{a_{-n}+b_{-n}i}{2}

我们将傅里叶级数之前的解带入上边
a_0=\frac{2}{T }\int_{0}^T f(t)dt \\ a_n=\frac{2}{T }\int_{0}^T f(t)cos(n \omega t)dt \\ b_n=\frac{2}{T }\int_{0}^T f(t)sin(n \omega t)dt

当n=0的时候：

n=0 \quad\quad C_n=\frac{a_0}{2}=\frac{2}{T }\int_{0}^T f(t)dt = \frac{1}{T }\int_{0}^T f(t)e^{-n \omega t}dt\\

当 n=1,2,3...的时候

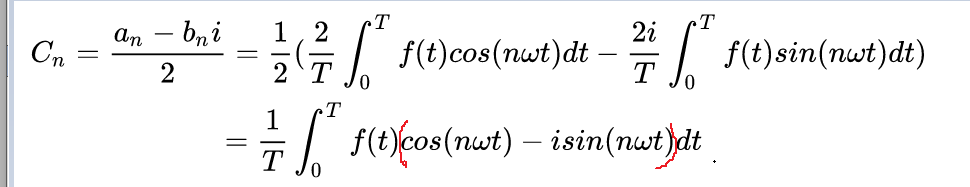
   这里因为cos是偶函数，sin是奇函数所以：

  当 n=-1,-2,-3...的时候

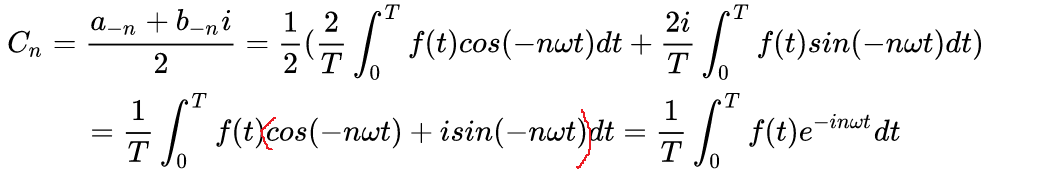
可以惊奇的发现，三种情况的解是一样的。所以对于任意周期函数，我们都可以写成:
f(t)=\sum_{n=-\infty}^{\infty}C_n e^{in\omega t} \\ C_n=\frac{1}{T }\int_{0}^T f(t)e^{-in \omega t}dt
但其中的每一项是什么意思呢？
还记得之前说的e^{i\theta}的本质吗？在圆上做圆周运动，那么e^{-in \omega t}也是在做周期运动了。那n\omega又是什么呢？
我们知道\omega=\frac{2\pi }{T}，所以我们可以把\omega 看成是以2\pi为单位的频率(正常来讲频率是\frac{1}{T})。而系数n是就可以看成是几倍的基频，正数是逆时针运动，负数就是顺时针运动。在图形上的反应就是，频率越高，转的越快了
，但其最小公共周期是一样的。
1倍基频

 
1倍频.gif

 

 

 

10倍基频

 
10倍频.gif

那么系数C_n怎么理解呢？前面说过ae^{i\theta}的系数a是代表e^{i\theta}运动的圆半径，这里C_n是复数是不是也能这样理解呢？其实粗糙来讲是可以这样理解的。
看个图，只管的理解下把

 
gif1.gif

 

上图中红色的向量相对于蓝色的向量只是多了系数C_n=\sqrt2+i\sqrt2,所以红色向量运动的半径就是2刚好是复数\sqrt2+i\sqrt2的模长乘以1，当然除此之外，红色向量的幅角也变大了些。这些都是因为复数的乘法性质---复数相乘表现为幅角相加，模长相乘。
这下，当有人和你说傅里叶变换是把时域变换到频域上，你应该就很容易理解是什么意思了。频域就是1倍，2倍，3倍.......的\omega,而每个 \omega都有自己的幅长C_n,当把这些所有的\omega相加，就得到时域中的图像。

更加生动有趣的介绍可以参见傅里叶分析之掐死教程，我这里是从数学的角度来介绍傅里叶变换。

3 推广到非周期函数上

目前该证明的都差不多了，还有最后一个任务，就是推广到非周期函数上。对于非周期函数，我们可以看成是周期无限远的函数，那也就是周期T变成\infty的时候傅里叶级数。随则T的变大w也就不断的减小，当T趋近于 \infty的时候，w也由1w,2w,3w......变成了\Delta w，那么很自然就需要对w 做积分。

我们先看下
\Delta w=(n+1)w-nw=w=\frac{2\pi}{T} \\ \frac{1}{T} =\frac{\Delta w}{2\pi}\\

当T趋近于 \infty的时候 我们可以得到：
\int_{0}^T f(t)dt \quad -> \quad \int_{-\infty}^\infty f(t)dt\\ \sum_{n=-\infty}^{\infty}\Delta w \quad -> \quad \int_{-\infty}^\infty dw
将这些带入 傅里叶级数,并且T趋近于\infty，就得到:
f(t)=\sum_{n=-\infty}^{\infty}\frac{1}{T }\int_{0}^T f(t)e^{-in \omega t}dt e^{in\omega t} \\ =\sum_{n=-\infty}^{\infty}\frac{\Delta w}{2\pi}\int_{0}^T f(t)e^{-in \omega t}dt e^{in\omega t}\\ =\frac{1}{2\pi} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty}f(t)e^{-i \omega t}dt e^{i\omega t}dw
其中画红圈的地方就是傅里叶变换

 
image.png


一般写成一个关于的函数，其实就相当于前面的:

 

而整个公式就是傅里叶逆变换，写成：
F^{-1}(t)=\frac{1}{2\pi} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty}f(t)e^{-i \omega t}dt e^{i\omega t}dw=\frac{1}{2\pi} \int_{-\infty}^{\infty} F(w) e^{i\omega t}dw

posted @ 2019-09-25 09:09  Hellozhu  阅读(1231)  评论(1)  编辑  收藏  举报