洛谷——P1495 【模板】中国剩余定理（CRT）/ 曹冲养猪

🌟 洛谷——P1495 【模板】中国剩余定理（CRT）/ 曹冲养猪

💡 在这个博客中，我将和大家分享我的思考和经验。
🎸🎸🎸

本栏将针对hdu题库的题目进行分析，由于网上已经有很多题解了，所以我也就针对做题过程进行一些分析，将一些有意思的地方分享出来

通过这个博客，我希望能够激发更多人对算法和Java的兴趣，也希望能够与更多有相同爱好的人交流和学习。

📖 内容

1. 题目介绍：

2. hdu--题目名字：

3. 题目介绍：

4. 有意思的知识：

---

🎈🎈🎈🎈🎈

题目介绍

洛谷--题目名字: P1495 【模板】中国剩余定理（CRT）/ 曹冲养猪

🎈🎈🎈🎈🎈

分析

典型的一道 中国剩余定理(孙子定理) 模板题
中国剩余定理（Chinese Remainder Theorem）是一种数论中的重要定理，它提供了一种解决模同余方程组的方法。模同余方程组是指一组形如：
x ≡ a₁ (mod m₁)
x ≡ a₂ (mod m₂)
...
x ≡ aₙ (mod mₙ)
其中，x是未知数，a₁、a₂、...、aₙ是给定的余数，m₁、m₂、...、mₙ是给定的不同模数。
中国剩余定理可以告诉我们，如果给定的模数两两互质（即它们没有公因数），那么存在一个解x，它在每个模数下都满足给定的余数。并且这个解在模数的乘积下也是唯一的。
解决模同余方程组的步骤如下：
使用欧几里得算法确保所有的模数两两互质。
计算模数的乘积N = m₁ * m₂ * ... * mₙ。
对于每个模数mᵢ，计算Nᵢ = N / mᵢ。
对于每个模数mᵢ，计算Nᵢ的逆元Nᵢ⁻¹，使得Nᵢ * Nᵢ⁻¹ ≡ 1 (mod mᵢ)。
计算解x = (a₁ * N₁ * N₁⁻¹ + a₂ * N₂ * N₂⁻¹ + ... + aₙ * Nₙ * Nₙ⁻¹) % N。
🎈🎈🎈🎈🎈

解题代码

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static long[] m = new long[100008]; // 用于存储输入的M值的数组
    static long mul = 1, X = 0; // mul用于存储所有M值的乘积，X用于存储最终的结果

    static long[] a = new long[100008]; // 用于存储输入的a值的数组
    static long[] Mi = new long[100008]; // 用于存储每个Mi值的数组

    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        long n = cin.nextInt(); // 输入n的值，代表有n个M和a值需要输入
        for (int t = 1; t <= n; ++t) {
            long M = cin.nextInt(); // 输入M的值
            m[t] = M; // 将M的值存储在m数组中
            mul *= M; // 计算所有M值的乘积
            a[t] = cin.nextInt(); // 输入a的值
        }
        for (int t = 1; t <= n; ++t) {
            Mi[t] = mul / m[t]; // 计算每个Mi值
            long[] x = new long[2]; // 创建一个长度为2的数组x，用于存储exgcd函数的结果
            Arrays.fill(x, 0); // 将数组x的所有元素初始化为0
            exgcd(Mi[t], m[t], x); // 调用exgcd函数计算x的值
            X += a[t] * Mi[t] * (x[0] < 0 ? x[0] + m[t] : x[0]); // 计算最终结果X
        }
        System.out.println(X % mul); // 输出结果X对mul取模的值
    }

    static void exgcd(long a, long b, long[] x) {
        if (b == 0) {
            x[0] = 1;
            x[1] = 0;
            return;
        }
        exgcd(b, a % b, x); // 递归调用exgcd函数
        long z = x[0];
        x[0] = x[1];
        x[1] = (z - x[1] * (a / b)); // 根据扩展欧几里得算法更新x的值
    }
}

🎈🎈🎈🎈🎈

有意思的知识

中国剩余定理（Chinese Remainder Theorem）是数论中的一个重要定理。它提供了一种有效的方法来解决一组同余方程的问题。

具体来说，中国剩余定理适用于一组模数两两互质的同余方程。假设有一组同余方程：
x ≡ a₁ (mod m₁)
x ≡ a₂ (mod m₂)
...
x ≡ aₙ (mod mₙ)

其中，a₁, a₂, ..., aₙ是给定的整数，m₁, m₂, ..., mₙ是给定的不同的正整数。根据中国剩余定理，如果这组同余方程满足两两互质的条件，那么存在唯一的解 x，且该解在模 m₁ × m₂ × ... × mₙ 的范围内。

中国剩余定理的应用非常广泛，特别是在密码学、编码理论和计算机科学中。它不仅可以用于解决同余方程的问题，还可以用于模数很大的情况下进行高效的计算。

附上潦草的草稿，忽略字迹

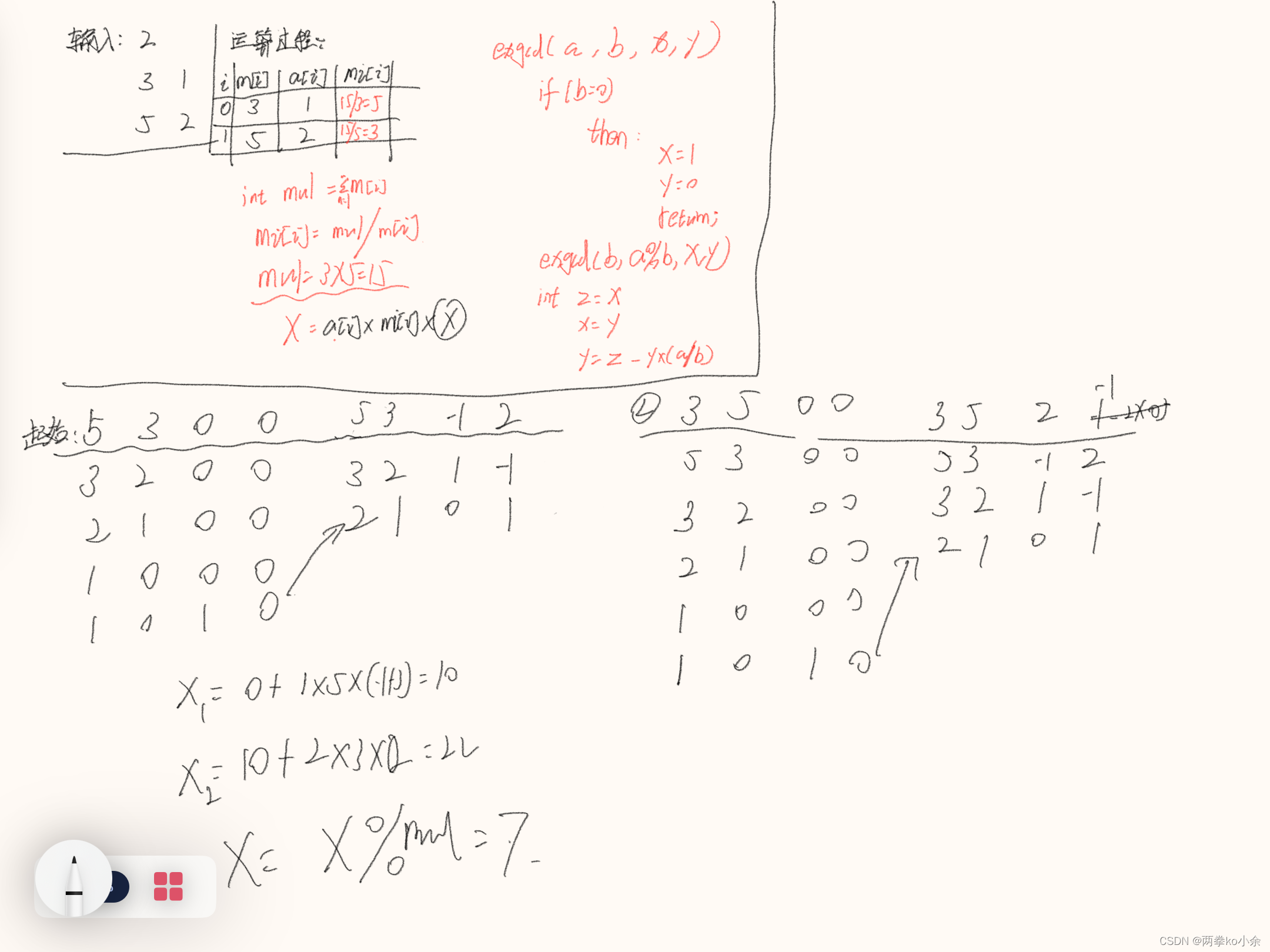
💭 结论

🎈🎈🎈🎈🎈
通过这个博客，我希望能够激发更多人对算法和Java的兴趣，也希望能够与更多有相同爱好的人交流和学习。

如果你对这题感兴趣，欢迎点击       P1495 【模板】中国剩余定理（CRT）/ 曹冲养猪。

感谢你的阅读！🙏

CSDN链接：洛谷——P1495 【模板】中国剩余定理（CRT）/ 曹冲养猪