本文讨论的是惠斯通电桥与热电阻的实际应用,不讨论理论知识,关于惠斯通电桥的理论知识请看这篇文章:https://zhuanlan.zhihu.com/p/267085334
1. 四分之一桥
使用Multisim仿真,搭建一个电桥,其中R2,R3,R4都为120Ω,R1是阻值随温度变化的电阻,假设R1的电阻为250Ω(因为温度变化导致电阻增加了130Ω),假设Vs为2.5V,此时根据公式Vo = Vs * (R2 / (R1 + R2) - R4 / (R3 + R4))计算得出,Vo ≈ -439mV,仿真结果如下:
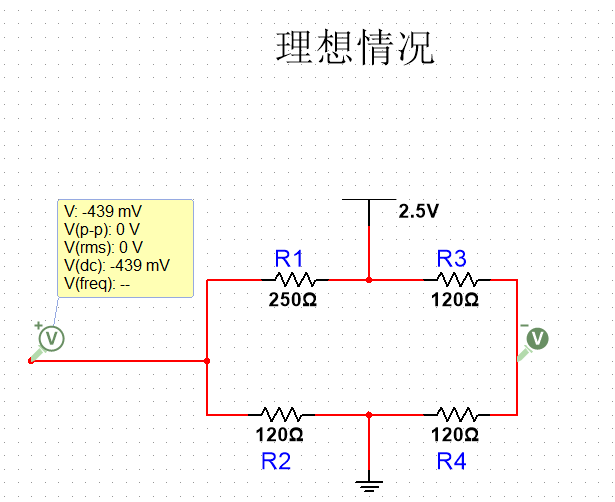
仿真结果与计算值相同。意思就是如果我们知道Vo的电压为-439mV,那么我们就知道R1增加了130Ω,进而可以算出温度变化。
但是实际情况往往是R1会拉很长的线连出去,线上也是有电阻的,并且线上的电阻也是随温度变化的(任何材料的电阻都会随温度变化而变化),那么实际的模型就会变成下面的模型:
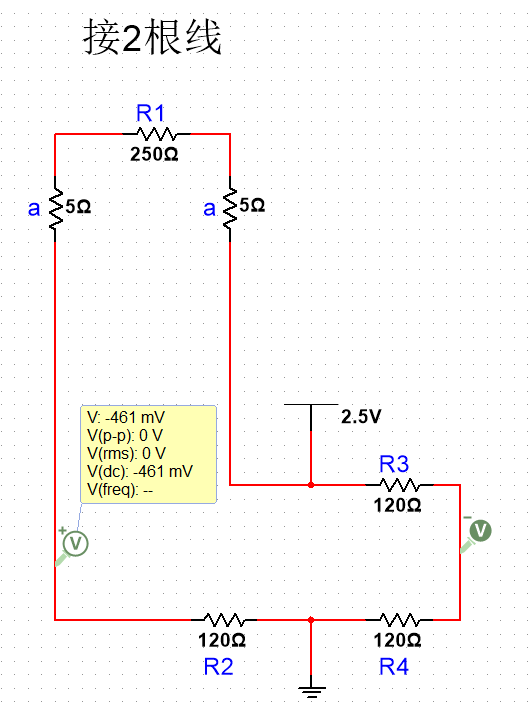
a等效线上的电阻,此时Vo为-461mV,我们认为R1的电阻增加了140Ω,而实际上只增加了130Ω,有10Ω是导线引入的,这样就带来了误差。
有一个方法可以减小这种误差,在R1的其中一端引出2根导线,按照下图的接法连接:
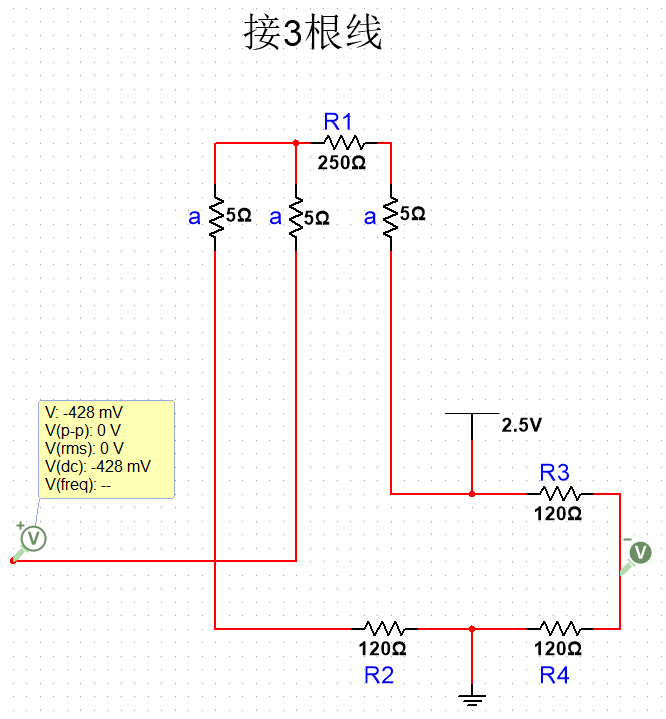
这样得到的Vo是-428mV,当R2=R3=R4时,这3种情况Vo的计算方法分别为:
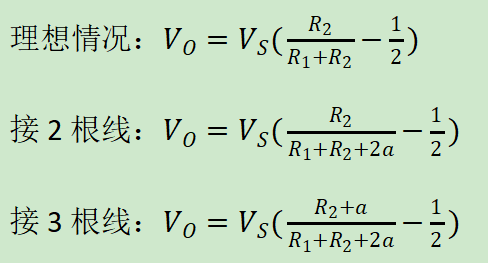
结果是:
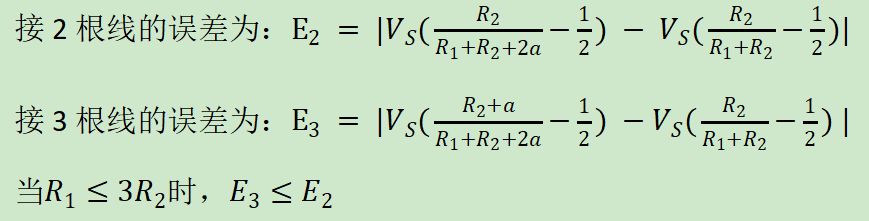
并且通过仿真也验证了,当R1=3R2时,2根线和3根线的误差相同,如下图:
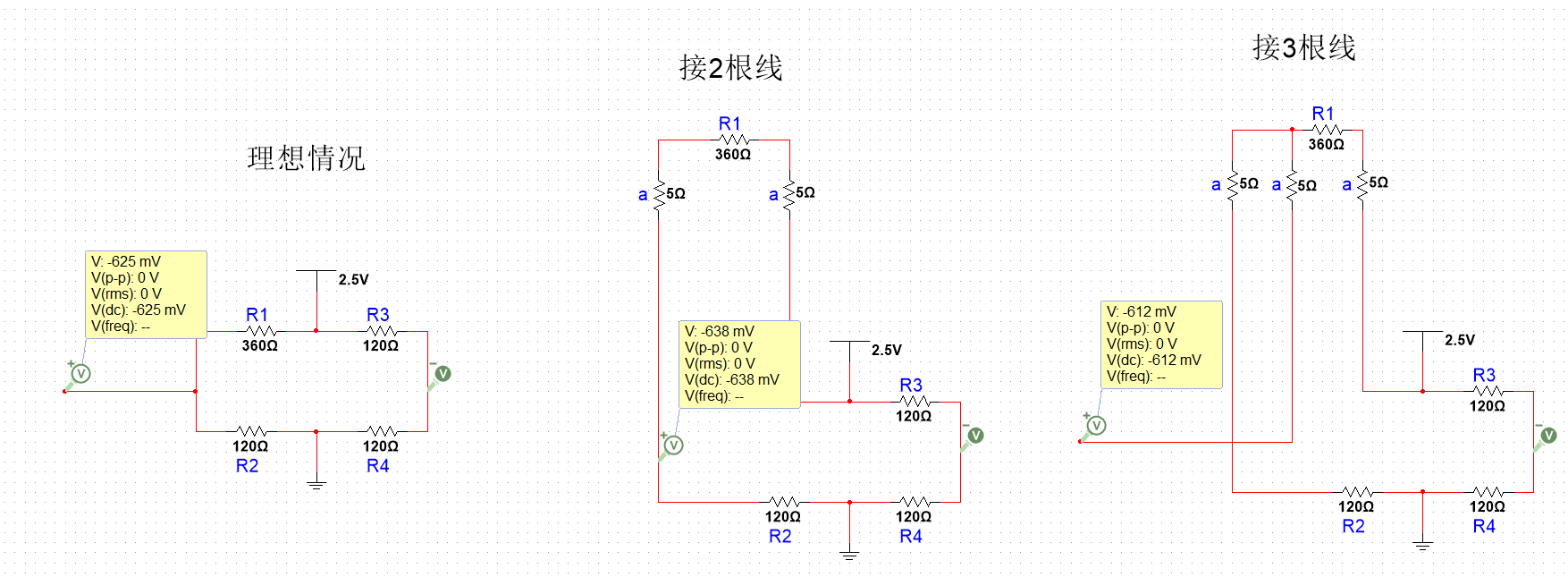
如果传感器接到R2的位置,用同样的方法计算得出,当R2≤3R1时,接3根线的误差才会比接2根线的误差更小,R3,R4同理。
也就是说,“使用四分之一桥,3根线的接法误差比2根线的接法误差更小”这句话是有前提条件的,前提条件就是变化的电阻不能比其他电阻的3倍要大,因此必须根据温度的变化范围去选择合适的阻值,否则效果会更差。
在实际使用时按照理想情况去计算,无论将变化的电阻接到R1还是R2的位置,Vo的值与可变电阻之间的关系都是反比例函数,并且接R1和接R2时他们的导数互为相反数,结论就是将任何一个电阻充当可变电阻,它们的精度都是相同的。因此不需要考虑到底将桥中哪个电阻充当可变电阻,因为它们都是一样的。
并且根据反比例函数的性质可以知道,当电阻的值越大时,导数的绝对值越小,意味着电桥(Vo)对电阻的变化越不敏感(电桥中任何一个电阻都是如此)。因此如果想要电桥的精度更高,那么电阻的选取要尽可能小,但同时要满足可变电阻最大值的3倍比其他固定电阻的值要大。
2. 热电阻温度与阻值计算
先说一下热电阻的型号定义,以PT100举例,PT指的是铂,100指的是该电阻在0℃时呈现的阻值为100Ω,那么CU50指的就是该电阻的材料是铜,在0℃时的阻值为50Ω。
铂热电阻(常见的如PT100,PT1000等)温度与阻值的关系为 RT = R0(1 + AT + BT² + C(T-100)T³) ,铜热电阻(常见的有CU50等)温度与阻值的关系为 RT = R0(1 + AT + BT(T-100) + C(T-100)T²),其中R0表示该电阻在0℃时的阻值,单位Ω,对于不同的电阻A,B,C的值会不同,如下:
| PT100 | PT1000 | CU50 | |
| R0 | 100 | 1000 | 50 |
| A | 0.0039083 | 0.0038623139728 | 0.00428 |
| B | -0.0000005775 | -0.00000065314932626 | -0.0000000931 |
| C |
当T≤0时 -0.000000000004183 当T>0时,0 |
0 | 0.00000000123 |
网上的那些分度表都是用这个公式生成的,下面的程序可以直接生成这3种型号的分度表:
1 #include <stdio.h> 2 #include <sys/types.h> 3 #include <fcntl.h> 4 #include <sys/stat.h> 5 #include <math.h> 6 #include <string.h> 7 8 /* 定义热电阻的型号 */ 9 //char RES_TYPE[16] = "PT100"; 10 //char RES_TYPE[16] = "PT1000"; 11 char RES_TYPE[16] = "CU50"; 12 13 /** 14 * \brief 铂热电阻温度与阻值的关系为 RT = R0(1 + AT + BT² + C(T-100)T³) 15 * 铜热电阻温度与阻值的关系为 RT = R0(1 + AT + BT(T-100) + C(T-100)T²) 16 * 其中R0表示该电阻在0℃时的阻值,单位Ω 17 * 对于不同的电阻A,B,C的值会不同 18 */ 19 20 int main(int argc, const char *argv[]) 21 { 22 double R0, A, B, C; 23 double min_t, max_t, step; /* min_t是最小测量温度,max_t是最大测量温度,step是温度步长 */ 24 double result = 0; 25 double i, j; 26 27 int k; 28 int fd; 29 char buff[256] = { 0 }; 30 char acc[16] = { 0 }; /* 打印精度 */ 31 32 if (argc == 2) { 33 strcpy(RES_TYPE, argv[1]); 34 } 35 36 if (!strcmp(RES_TYPE, "PT100")) { 37 R0 = 100; 38 A = 0.0039083; 39 B = -0.0000005775; 40 C = -0.000000000004183; 41 min_t = -200; 42 max_t = 660; 43 step = 1; 44 strcpy(acc, "%.02f,"); /* 保留2位小数 */ 45 } else if (!strcmp(RES_TYPE, "PT1000")) { 46 R0 = 1000; 47 A = 0.0038623139728; 48 B = -0.00000065314932626; 49 C = 0; 50 min_t = -50; 51 max_t = 300; 52 step = 0.1; 53 strcpy(acc, "%.03f,"); /* 保留3位小数 */ 54 } else if (!strcmp(RES_TYPE, "CU50")) { 55 R0 = 50; 56 A = 0.00428; 57 B = -0.0000000931; 58 C = 0.00000000123; 59 min_t = -50; 60 max_t = 150; 61 step = 1; 62 strcpy(acc, "%.03f,"); /* 保留3位小数 */ 63 } else { 64 printf("暂不支持该型号!\n"); 65 return 0; 66 } 67 68 //printf("A = %f\nB = %f\nC=%f\n", A, B, C); //可以看浮点数有截断误差 69 70 strcpy(buff, RES_TYPE); 71 strcat(buff, "热电阻常用阻值对应表.csv"); 72 fd = open(buff, O_CREAT | O_RDWR | O_TRUNC, 0666); 73 if (fd < 0) { 74 printf("open failed\n"); 75 return 0; 76 } 77 memset(buff, 0, sizeof(buff)); 78 79 /* 写入横轴 */ 80 strcpy(buff, "温度℃,"); 81 write(fd, buff, strlen(buff)); 82 for (k = 0; k < 10; k++) { 83 sprintf(buff, "%f,", k*step); 84 write(fd, buff, strlen(buff)); 85 } 86 write(fd, "\r\n", 2); 87 88 for (i = min_t; i <= 0; i += 10 * step) { 89 sprintf(buff, "%f,", i); 90 write(fd, buff, strlen(buff)); 91 for (j = 0; j < 10; j += step) { 92 if (!strcmp(RES_TYPE, "CU50")) { 93 result = R0 * (1 + A * (i - j) + B * (i - j) * (i - j - 100) + C * (i - j - 100) * (i - j) * (i - j)); 94 } else { 95 //result = R0 * (1 + A * (i - j) + B * pow((i - j), 2) + C * (i - j - 100) * pow((i - j), 3)); 96 result = R0 * (1 + A * (i - j) + B * (i - j) * (i - j) + C * (i - j - 100) * (i - j) * (i - j) * (i - j)); 97 } 98 sprintf(buff, acc, result); 99 write(fd, buff, strlen(buff)); 100 if (i == min_t) { 101 break; 102 } 103 } 104 write(fd, "\r\n", 2); 105 } 106 for (i = 0; i <= max_t; i += 10 * step) { 107 sprintf(buff, "%f,", i); 108 write(fd, buff, strlen(buff)); 109 for (j = 0; j < 10; j += step) { 110 if (!strcmp(RES_TYPE, "CU50")) { 111 result = R0 * (1 + A * (i + j) + B * (i + j) * (i + j - 100) + C * (i + j - 100) * (i + j) * (i + j)); 112 } else { 113 //result = R0 * (1 + A * (i + j) + B * pow((i + j), 2)); 114 result = R0 * (1 + A * (i + j) + B * (i + j) * (i + j)); 115 } 116 sprintf(buff, acc, result); 117 write(fd, buff, strlen(buff)); 118 if (i == max_t) { 119 break; 120 } 121 } 122 write(fd, "\r\n", 2); 123 } 124 125 close(fd); 126 127 return 0; 128 }
有几个需要注意的点:
1. 因为浮点数存在截断误差,所以通过这个程序计算出来的值,与真实值略有出入(可以忽略);
2. 通过这个方法计算出来的PT100和CU50的表与网上的其他表一致,但是PT1000不一致(差别很小),经过验证发现网上的PT1000的分度表实际上是用PT100的参数计算出来的,我简直呵呵了,公式都摆在那,那些人都不自己算一遍的吗。
3. PT100和PT1000精度比较
通过上一节算出来,当温度从0℃增加到1℃时,PT100的电阻增加0.39Ω,PT1000的电阻增加3.862Ω(网上的表是3.908Ω),可见PT1000增加的电阻是PT100的10倍,是不是意味着PT1000精度是PT100的10倍呢?从第1节的计算结果得出,当电阻值越大时,惠斯通电桥对电阻的变化越不敏感,它们是一个反比例函数的关系。
假设我们需要测量的温度不会大于150℃,此时PT100的阻值是157.33欧姆,PT1000的阻值是1564.651Ω,根据第1节算出来的电阻选取规则,使用PT100时,其他电阻选用56Ω比较合适,使用PT1000时其他电阻选用560Ω比较合适。
假设PT100的电阻是k,那么相同温度下PT1000的电阻就为10k,Vo的值用下面的公式计算:
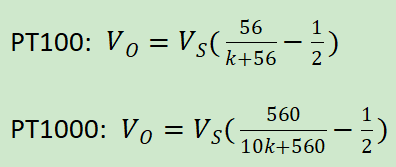
这时就发现一个问题,Vo的值是一模一样的。也就是说,如果使用惠斯通电桥测温度,PT100和PT1000在精度上没有任何差别。
4. 放大倍数及电路确定
以PT100为例,固定电阻为56Ω,假设使用温度范围为-20℃~150℃,PT100的阻值变化范围为92.16Ω~157.33Ω,Vo的值范围为305mV~594mV(取绝对值)。而一般的ADC能采集0~3.3V的电压(单端电压),因此为了提高精度,可以将电压放大5倍(需要选用差分放大器),这样电压范围会变为1.525V~2.97V,更好的利用的ADC的采集范围,以此提高精度。
可以使用INA128U对信号进行放大,INA128U的放大倍数为1+50K/RG,取RG为12.5k,那么放大倍数就是5,仿真如下图:
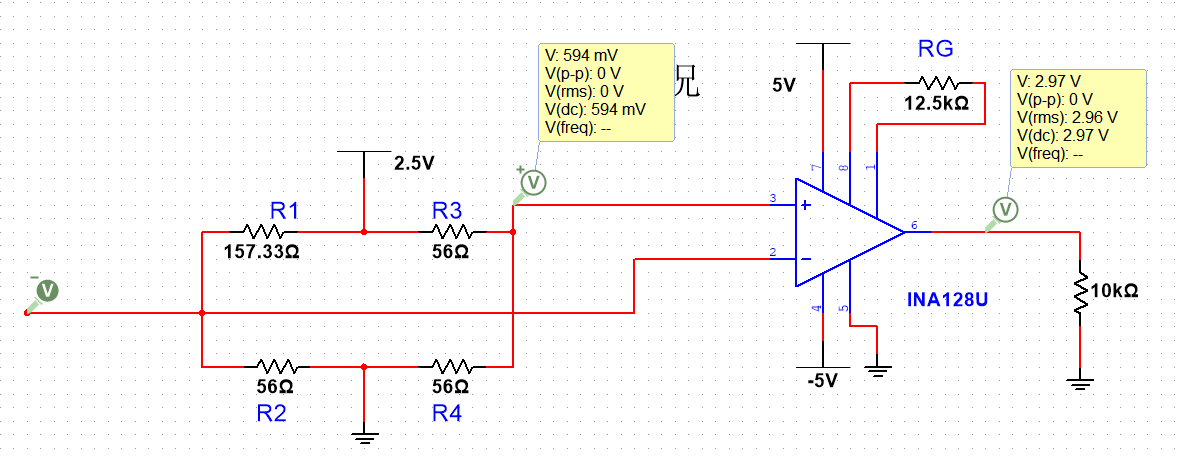
其中INA128U的6号引脚输出电压是经过放大后的电压值再加上5号引脚的电压,因此,如果想要继续提示精度,可以算出温度变化范围内电压的差值,为594-305=289mV,为了尽可能达到3.3V的满量程,可以将放大倍数调整到11倍,同时在5号引脚施加一个偏置电压,让INA128U的输出电压落在0~3.3V的区间内,按照下图所示方法连接,当温度达到最大值150℃时,放大器输出最小值(-0.594*11)+6.6=0.066V,当温度达到最小值-20℃时,放大器输出(-0.305*11)+6.6=3.245V
仿真结果与计算结果基本一致:
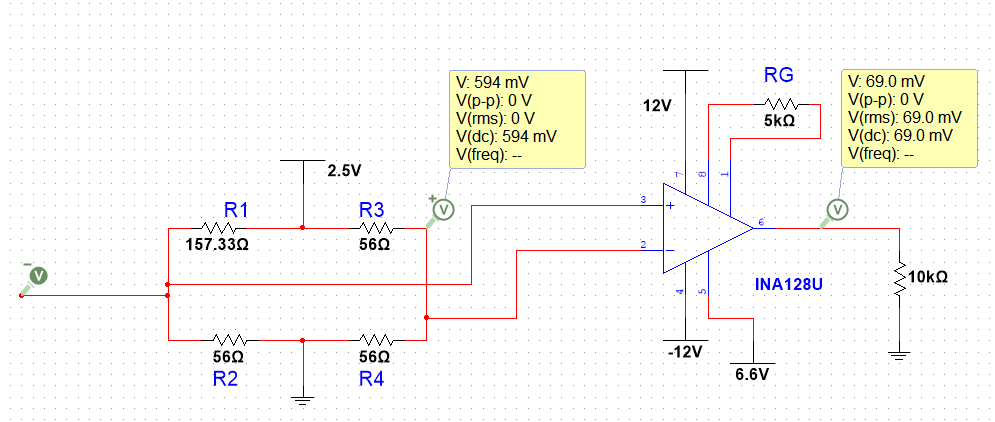

5. 使用惠斯通电桥与电阻分压测电阻的优点分析
5.1 从计算方法考虑
热敏电阻使用3线制接法,先看直接分压的情况,如下图:
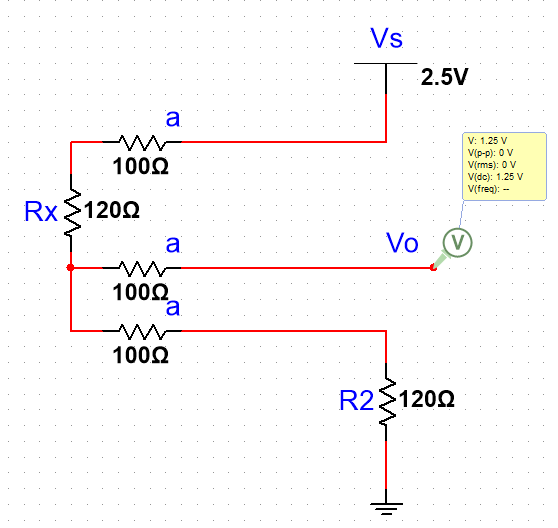
Vo的计算公式为:
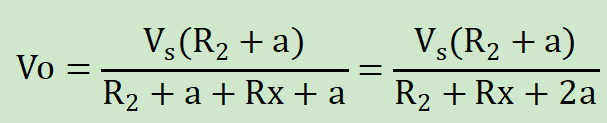
可见Vo是Rx的反比例函数。随着Rx的增加,Vo的变化会越来越不明显。
再看惠斯通电桥的情况:
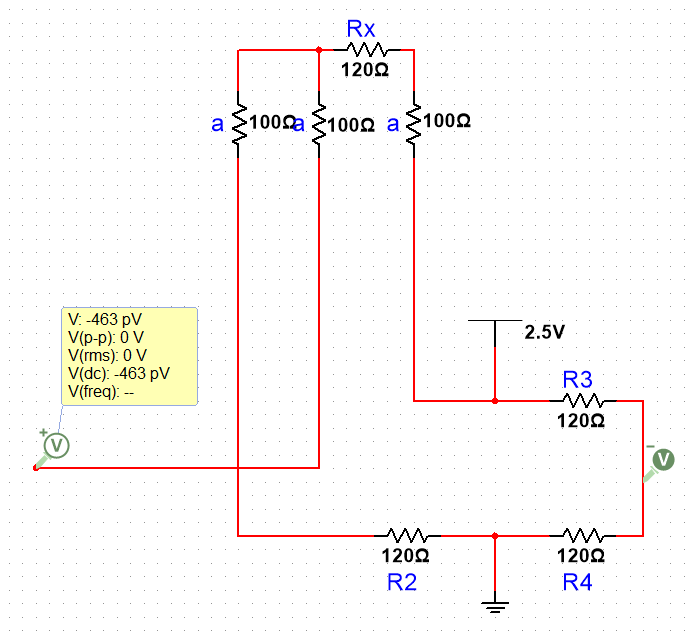
Vo的计算公式为:
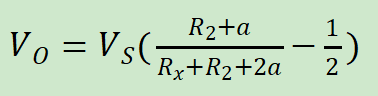
这与电阻直接分压的算法差不多,只不过是括号里多减了个1/2,而且它们的导数是相同的,并且它们受到线上电阻a的影响是一样的,这意味着从计算方法上看,惠斯通电桥法与电阻分压法是完全一样的。
5.2 从特殊情况考虑
我们知道惠斯通电桥有一种平衡状态,就是Vo为0的情况,此时有一个特性,就是:
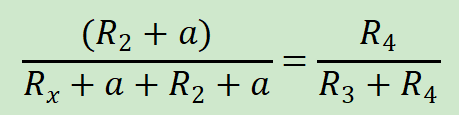
一般让R2,R3,R4都相等,记作R,此时
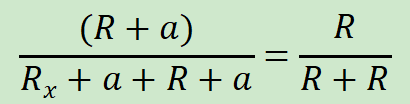
化简之后得到Rx=R,此时式子里没有a,也就是说当电桥平衡时,即Vo=0时,惠斯通电桥可以完全消除线上电阻的影响,得到的结果是最精确的。
但是电阻分压法就不能有这个优点吗?
电阻分压法的特殊情况是Vo=1/2Vs,此时Rx+a=R2+a,Rx=R2,同样消除了线上电阻的影响。
但是!当惠斯通电桥达到平衡状态时,不需要考虑参考电压Vs,无论Vs的值为多少,Vo的值都是0,而电阻分压法的平衡状态是Vo=1/2Vs,Vo的值会受Vs的影响。所以惠斯通电桥真正的优点是:在平衡状态时消除了参考电源的影响
不过话又说回来,因为被测电阻是变化的,要使惠斯通电桥达到平衡状态,需要改变其他3个电阻的值,在实际情况下这是不现实的。
6. 推荐使用方法(使用运算放大器)
既然惠斯通电桥的优点那么不明显,那就直接用简单的电阻分压法吧。
将PT100串联一个56Ω的电阻测量2个电阻之间的电压,当温度变化范围为-20℃~150℃时,PT100的阻值变化范围为92.16Ω~157.33Ω,Vo的值范围为656mV~945mV,假设ADC的采样范围为0~3.3V,那么可以将电压放大3倍,得到的电压范围为1.968V~2.835V,这样虽然将采样精度提高了3倍,但是0~1.968V这个区域浪费了。最好的情况就是656mV~945mV这个范围刚好能对应上0~3.3V的范围,这时就要用运算放大器了,将其作为一个减法器放大。具体接法如下图:
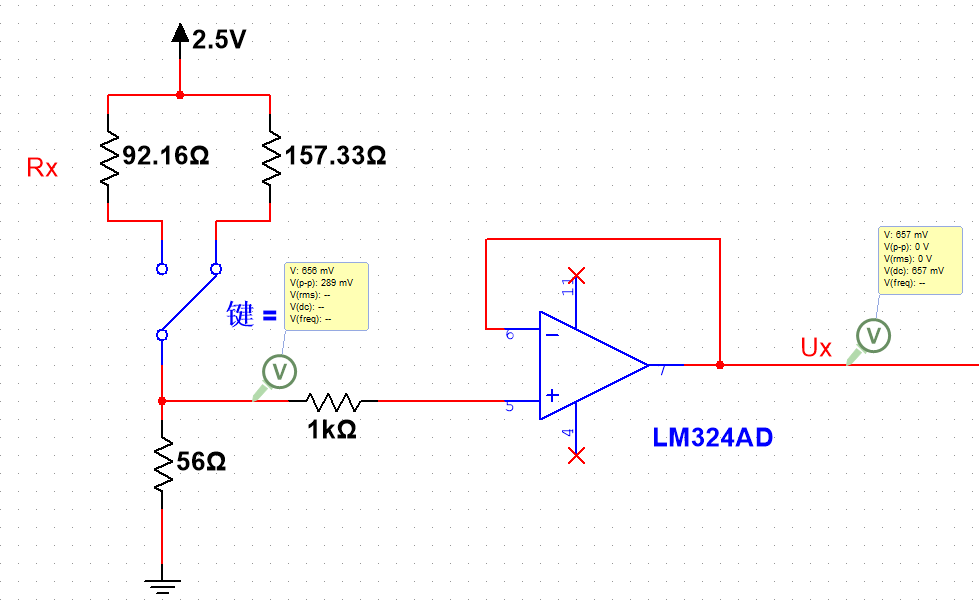
必须用电压跟随,否则Ux的值会随着放大倍数的改变而改变。
Ux的值最小为657mV,那么就在另一端造一个657mV出来,如下图:

为了留点余量,这里造出来的电压是639mV。然后将这两个电压接到减法器里,如下图:
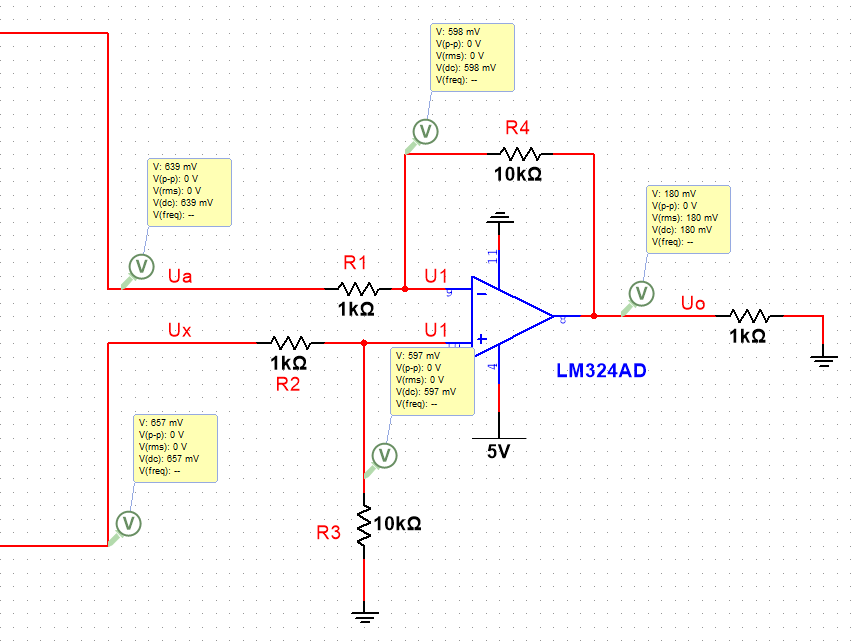
根据运放的特性,得到以下2个式子:

联立化简得到如下式子:

现在认为制造一种特殊情况,就是R1=R2,R3=R4,那么上面的式子就可以化简为:
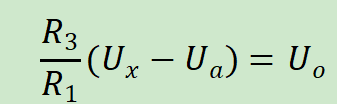
如果再让R3=R1,那么此时Uo=Ux-Ua,这就是减法器。
但是我们还是要利用一个R3/R1这个数,因为Ua是我们造出来的电压,它等于Ux的最小值,此时Uo的值为0,而当,Ux变化到945mV时,我们希望Uo的值尽可能接近3.3V,那么就可以取R3=11R1,此时放大倍数为11倍,最大输出电压为3.179V,尽可能的利用了ADC的采样范围。
而实际情况需要留一些余量,按照上面的接法,让Ua的值为639mV,比Ux的最小值再小一点,放大倍数设为10倍,理论上输出电压值范围在180mV~3.06V之间,尽可能的利用了ADC的采样范围。
补充:
虽然理想运放最大输出电压接近电源电压,但是要根据实际情况而定,比如我使用的LM324,手册上说的是:Large Output Voltage Swing: 0V to VCC-1.5V,因此他的输入电源要大于3.3+1.5=4.8V,取5V比较合适。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号