题解 UVA12459 Bees' ancestors

题解 UVA12459 Bees' ancestors

这里提供一份良（mei）心（yong）的：

题目翻译

题目描述

玛雅是一只乐于助人的蜜蜂。威利是一只雄蜂兼玛雅的好朋友。他发现他没有父亲，而且他对此非常忧虑。玛雅知道雌蜂有两个父母（一个父亲一个母亲），但是雄蜂有母亲但没有父亲。这是因为若一个卵是被没有受精的雌蜂产下的话，它会产出雄蜂，但是如果，一个卵是被雄蜂受精了的话，它会产出雌蜂。在玛雅和威利谈话之后，他开始思考他的祖先的数量。他有一个母亲。他同样有两个祖父母（一个祖母和一个祖父）。并且他有三个曾祖父母。因为威利很懒，他不想再算数了而且他想让你写出一个程序能计算出一代人的数量，计算出威利有多少祖先在那一代，假定祖先在每一层次都不相关联。

输入格式

输入一个正整数序列，每行一个数字代表第几代，'0'结束。输入数据的最大值为80。

输出格式

对于每个输入，程序必须输出威利在这一代所有的祖先的数量。

题目思路

分析题意，我们可以得出如下图解：

（左列代表第几代，右列代表某代祖先数）

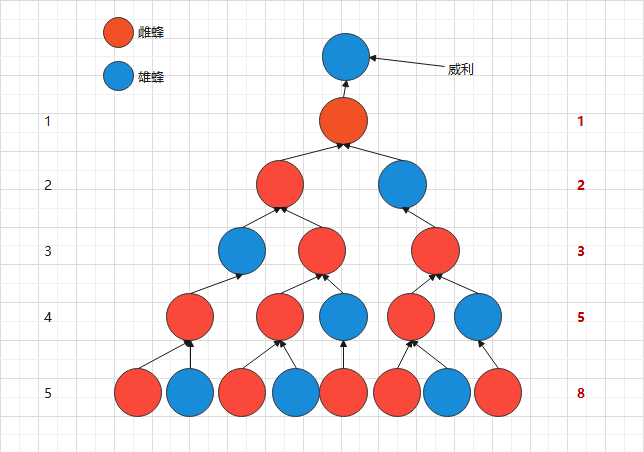
发现右列是裸的斐波那契数列第 \(n\) 项啊。

但为什么会是这样呢？这里给出最简单直（wu）观（nao）的代数证明方法：

---

设在任意一代，雌蜂的数量为 \(x\) ，雄蜂的数量为 \(y\) ，这一代用 \(P\) 表示，他的上一代用 \(F_1\) 表示，上上一代用 \(F_2\) 表示，因雌、雄蜂都需要由一个雌蜂产出，故 \(F_1\) 雌蜂数量为 \(x+y\) ，只有雌蜂需要由雄蜂和雌蜂一同产出，故 \(F_1\) 雄蜂数量为 \(x\) ，可得 \(F_1\) 蜜蜂总数为 \(2x+y\) 。

至此，我们好像已经得出一个直观的规律，若记录每一代雌蜂雄蜂数量，也可通过递推得出答案。

a[i]=a[i-1]+b[i-1];
b[i]=a[i-1];

cout<<a[n]+b[n];

「这就是你不能像我一样AKIOI的原因所在啊！」 ——zyz

我们来继续推一下，同理可得 \(F_2\) 的雌蜂数量为 \(2x+y\) 雄蜂数量为 \(x+y\) ，蜜蜂总数为 \(3x+2y\) ；

\[3x+2y=(x+y)+(2x+y) \]

发现 \(F_2\) 代蜜蜂总数等于 \(F_1\) 总数加上 \(P\) 总数，即斐波那契数列。

---

\(max_n=80\) ，暴力即可解决一切问题。

记得开 \(\textit{long long}\) 喔！

\(Code\)

#include<bits/stdc++.h>
using namespace std;
long long a[100]={0,1,2},n;
int main()
{
	for(int i=3;i<=88;i++)
		a[i]=a[i-1]+a[i-2];
	while(cin>>n)
	{
		if(!n) break;
		cout<<a[n]<<endl;
	}
	return 0;
}