学习笔记②
阶段一:基础算法和数据结构
二.DP:动态规划
- DP简介
- 记忆化搜索、LIS、LCS
- 线性dp、区间dp、背包dp、状压dp、概率dp等
参考链接:
算法-动态规划 Dynamic Programming--从菜鸟到老鸟
DP简介
动态规划( Dongtai Planning Dynamic Programming,简称DP)
是解决 “多阶段决策问题”的一种高效算法。
基本思路:
动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
分治思想
分治思想是一种解决复杂问题的策略,它包括以下四个主要步骤:
分解:将原始问题分解成若干个子问题,这些子问题通常是相同规模的,并且彼此独立。
解决:对每个子问题进行直接或递归的处理,直到子问题变得足够小以至于可以直接解决。
合并:将所有子问题的解组合起来,形成原问题的解。
停止条件:如果子问题的规模已经足够小,或者达到了设定的最大问题规模限制(如n),则返回子问题的解作为原问题的解。
分治思想适用于那些具有最优子结构性质的原问题,这意味着随着问题的分解,我们可以不断地减少问题的规模,最终使得问题变得足够小以便直接解决。如果子问题的规模仍然较大,我们继续对其进行进一步的分治。
经典例子:二分查找
分治算法的适用性取决于原问题的特点。如果原问题满足以下条件:
问题规模在一定条件下可以缩小到足够小;
可以被分解为若干个规模较小的相同子问题;
子问题的解可以合并为原问题的解;
子问题之间相互独立,没有公共子问题。
与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。
动态规划核心思想:
A : "1+1+1+1+1+1+1+1 =?"
A : "上面等式的值是多少"
B : 计算 "8"
A : 在上面等式的左边写上 "1+" 呢?
A : "此时等式的值为多少"
B : 很快得出答案 "9"
A : "你怎么这么快就知道答案了"
A : "只要在8的基础上加1就行了"
A : "所以你不用重新计算,因为你记住了第一个等式的值为8!动态规划算法也可以说是 '记住求过的解来节省时间'"
动态规划最核心的思想,就在于拆分子问题,记住过往,减少重复计算。

如何拆分问题,才是动态规划的核心。
而拆分问题,靠的就是状态的定义和状态转移方程的定义。这也是动态规划的本质所在。
例题解析:洛谷 P1255 数楼梯
题目描述
楼梯有 \(N\) 阶,上楼可以一步上一阶,也可以一步上二阶。
编一个程序,计算共有多少种不同的走法。
输入格式
一个数字,楼梯数。
输出格式
输出走的方式总数。
输入输出样例
输入 #1
4
输出 #1
5
说明/提示
对于 \(60%\) 的数据,\(N≤50\) ,
对于 \(100%\) 的数据,\(1≤N≤5000\) 。
- 要想跳到第10级台阶,要么是先跳到第9级,然后再跳1级台阶上去;要么是先跳到第8级,然后一次迈2级台阶上去。
- 同理,要想跳到第9级台阶,要么是先跳到第8级,然后再跳1级台阶上去;要么是先跳到第7级,然后一次迈2级台阶上去。
- 要想跳到第8级台阶,要么是先跳到第7级,然后再跳1级台阶上去;要么是先跳到第6级,然后一次迈2级台阶上去。
- ......
假设跳到第n级台阶的跳数我们定义为f(n),很显然就可以得出以下公式:
其中,我们从第10层台阶的计算公式推算到第9阶,再往前推到第8阶的过程,就是状态之间的转移,依照此规律,我们可以得到一个通用的状态转移方程:
那 \(f(2)\) 或者 \(f(1)\) 等于多少呢?
当只有2级台阶时,有两种跳法,第一种是直接跳两级,第二种是先跳一级,然后再跳一级。即 \(f(2) = 2\) ;当只有1级台阶时,只有一种跳法,即 \(f(1) = 1\) ;
因此可以用递归去解决这个问题:
int dfs(int n)
{
if(n==1)
return 1;
if(n==2)
return 2;
return dfs(n-1)+dfs(n-2);
}
然而我们在洛谷提交代码,只拿到了50tps,TLE(时间超限)了五个点。
为什么超时了呢?递归耗时在哪里呢?先画出递归树看看:
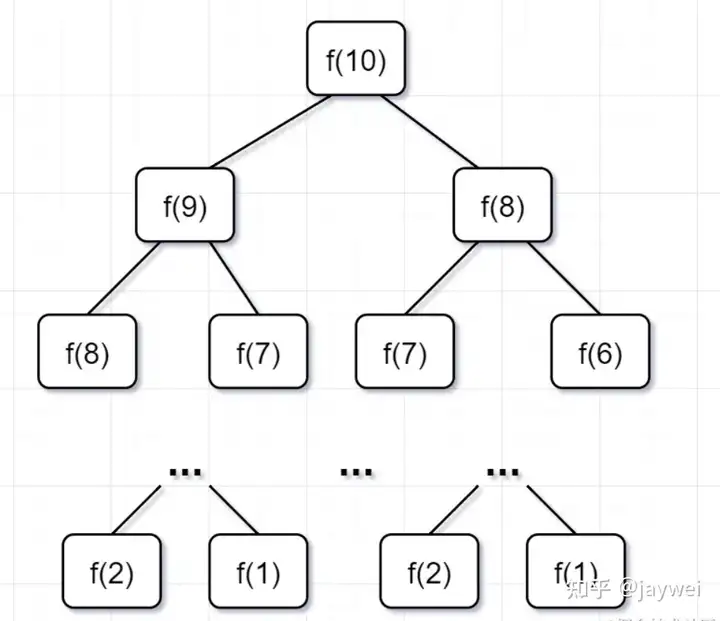
- 要计算原问题 f(10),就需要先计算出子问题 f(9) 和 f(8)
- 然后要计算 f(9),又要先算出子问题 f(8) 和 f(7),以此类推。
- 一直到 f(2) 和 f(1),递归树才终止。
我们先来看看这个递归的时间复杂度吧:
递归时间复杂度 = 解决一个子问题时间*子问题个数
- 一个子问题时间 = \(f(n-1)+f(n-2)\) ,也就是一个加法的操作,所以复杂度是 O(1);
- 问题个数 = 递归树节点的总数,递归树的总节点 = \(2^n-1\) ,所以是复杂度 \(O(2^n)\)
因此,爬台阶,递归解法的时间复杂度 \(= O(1) \times O(2^n) = O(2^n)\) ,就是指数级别的,爆炸增长的,如果n比较大的话,超时很正常的了。
回过头来,你仔细观察这颗递归树,你会发现存在大量重复计算,比如 \(f(8)\) 被计算了两次,\(f(7)\) 被重复计算了3次...所以这个递归算法低效的原因,就是存在大量的重复计算!
既然存在大量重复计算,那么我们可以先把计算好的答案存下来,即造一个备忘录,等到下次需要的话,先去备忘录查一下,如果有,就直接取就好了,备忘录没有才开始计算,那就可以省去重新重复计算的耗时啦!这就是带备忘录的解法。
带备忘录的递归解法(自顶向下)
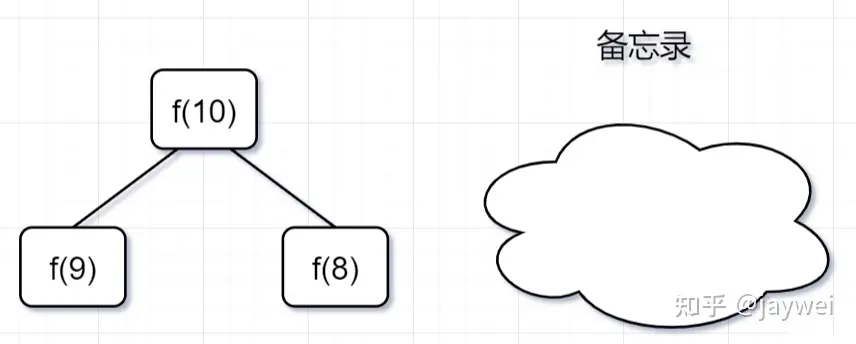
一般的题目中,常使用数组作为备忘录储存信息。
- 第一步,f(10)= f(9) + f(8),f(9) 和f(8)都需要计算出来,然后再加到备忘录中,如下:
- 第二步, f(9) = f(8)+ f(7),f(8)= f(7)+ f(6), 因为 f(8) 已经在备忘录中啦,所以可以省掉,f(7),f(6)都需要计算出来,加到备忘录中~
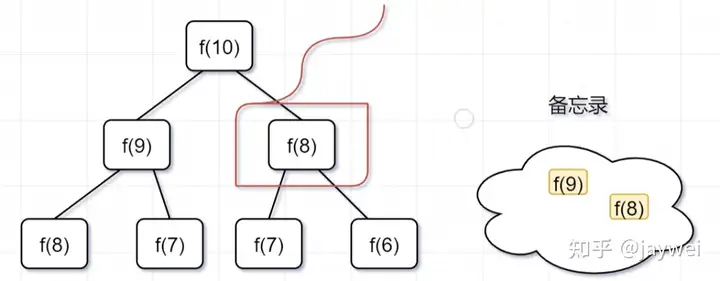
- 第三步, f(8) = f(7)+ f(6),发现f(8),f(7),f(6)全部都在备忘录上了,所以都可以剪掉。
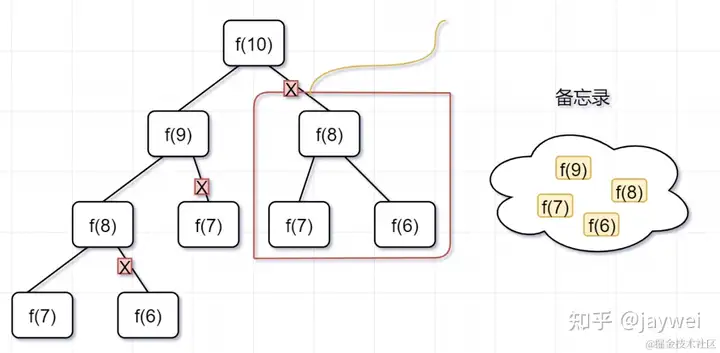
- 所以呢,用了备忘录递归算法,递归树变成光秃秃的树干咯,如下:
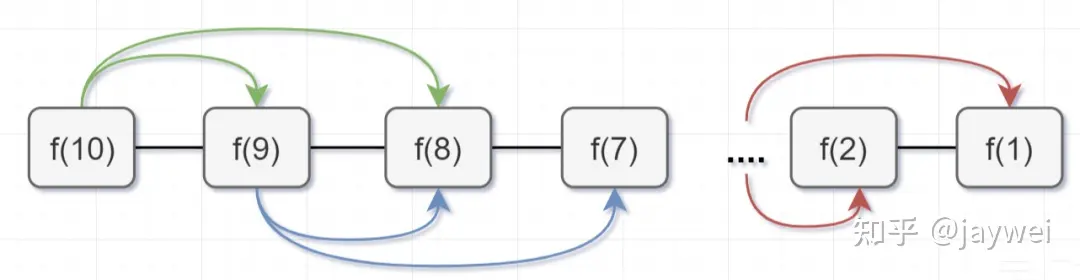
带备忘录的递归算法,子问题个数=树节点数= \(n\) ,解决一个子问题还是 \(O(1)\) ,所以带备忘录的递归算法的时间复杂度是 \(O(n)\) 。接下来呢,我们用带备忘录的递归算法去撸代码,解决这个数楼梯阶问题的超时问题咯~,代码如下:
long long dfs(int n)
{
if(n==0) return 0;
if(n<=2) return n;
if(a[n]>0) return a[n];
else
{
a[n]=dfs(n-1)+dfs(n-2);
return a[n];
}
}
此时,在时间复杂度上我们就过关了。其实这种算法也是记忆化搜索,顾名思义,为每一次搜索注入记忆,记录以前得到的值在后面的搜索中直接利用,从而避免了重复的步骤。
自底向上的动态规划
动态规划跟带备忘录的递归(记忆化搜索)解法基本思想是一致的,都是减少重复计算,时间复杂度也都是差不多。但是呢:
- 带备忘录的递归,是从f(10)往f(1)方向延伸求解的,所以也称为自顶向下的解法。
- 动态规划从较小问题的解,由交叠性质,逐步决策出较大问题的解,它是从f(1)往f(10)方向,往上推求解,所以称为自底向上的解法。
动态规划有几个典型特征,最优子结构、状态转移方程、边界、重叠子问题。在数楼梯问题中:
- f(n-1)和f(n-2) 称为 f(n) 的最优子结构
- f(n)= f(n-1)+f(n-2)就称为状态转移方程
- f(1) = 1, f(2) = 2 就是边界啦
- 比如f(10)= f(9)+f(8),f(9) = f(8) + f(7) ,f(8)就是重叠子问题。
我们来看下自底向上的解法,从f(1)往f(10)方向,想想是不是直接一个for循环就可以解决啦,如下:
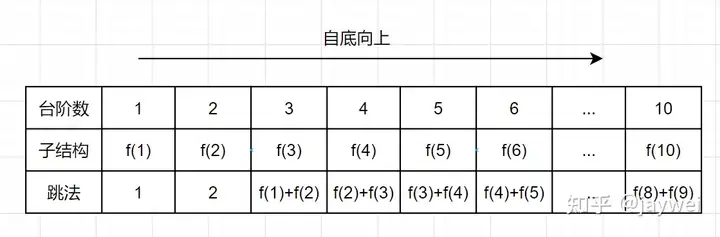
带备忘录的递归解法,空间复杂度是O(n),但是仔细观察上图,可以发现,f(n)只依赖前面两个数,所以只需要两个变量a和b来存储,就可以满足需求了,因此空间复杂度是O(1)。这样一来既节省了时间又节省了空间。
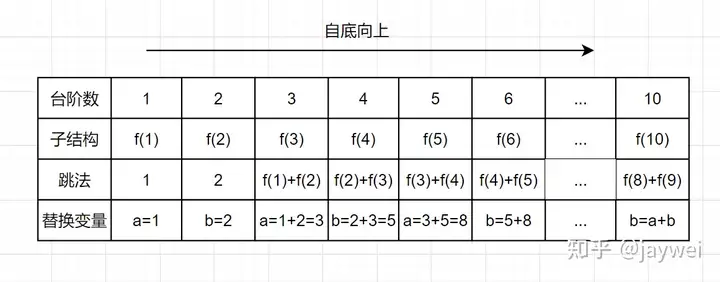
代码如下:
for(int i=3;i<=n;i++)
{
ans=a+b;
a=b,b=ans;
}
cout<<ans;
动态规划的解题套路
我们前面提到了分治法和dp的区别,那么什么时候可以使用dp呢?
这就不得不提到dp的两个条件了。
-
最优子结构性质。一个最优化策略的子策略总是最优的。
-
无后效性。某阶段的状态一旦确定,则此后过程的演变不再受此前各状态及决策的影响。即每个当前状态会且仅会决策出下一状态,而不直接对未来的所有状态负责。
也就是说,“未来与过去无关”,当前的状态是此前历史的一个完整的总结,此后的历史只能通过当前的状态去影响过程未来的演变。
可以浅显地理解为:
\[Future\ never\ has\ to\ do\ with\ past\ time\ , \]\[but\ present\ does. \]现在决定未来,未来与过去无关。
而对于子问题的重叠性,动态规划实质上是一种以空间换时间的技术,它在实现的过程中,不得不存储产生过程中的各种状态,所以它的空间复杂度要大于其他的算法。选择动态规划算法是因为动态规划算法在空间上可以承受,而搜索算法在时间上却无法承受,所以我们舍空间而取时间。
动态规划的解题思路
方式:
正推(自底向上):
从初始状态开始,通过对中间阶段的决策的选择,达到结束状态。我们也称之为递推。
倒推(自顶向下):
从结束状态开始,通过对中间阶段的决策的选择,达到初始状态。我们可以称之为记忆化搜索。
步骤
1. 确定状态和状态变量
除了“问题的规模”这一直接的状态,还应考虑一些附加的,用来满足“最优子结构”性质。
2. 确定决策并写出状态转移方程
根据状态的实际意义去转移,一般有两种考虑方式:“如何分解”和“如何合并”,根据实际选择。状态值转移方式有时并不容易直接看出,当前状态也许和多个子结构有关,其中的系数也不确定,一般先采用穷举法在演草纸上一步一步推导去找到规律。
3. 寻找边界条件
这一步不容小觑。边界的数量和数值都是随题目变化的,需要依题意而定。
4. 分析复杂度
时间复杂度=状态总数x单次转移复杂度
5. 编程实现程序(正推或倒推)
注意各类边界,注意数据类型(爆int?double精度?)
例如上文讲到的例题,当把“正解”提交后,我得到了一个暖暖的60分。原因无他,这题的输出值太大,无符号long long也容不下,需要用到人人见了都要唇角含笑的高精度。