红黑树的删除操作---以JDK源码为例
删除操作需要处理的情况:
1.删除的是红色节点,则删除节点并不影响红黑树的树高,无需处理。
2.删除的是黑色节点,则删除后,删除节点所在子树的黑高BH将减少1,需要进行调整。
节点标记:
- 正在处理的节点x
- 父节点p
- 兄弟节点s(sibling)
- 左侄子LN(Left Nephew)
- 右侄子RN(Right Nephew)
无需调整的情况(向上回溯时)
- 当前x为根节点,无论root为什么颜色,都将root染黑,rootOver。
- 当前x为红色,将其染黑,redOver。(增加所在子树黑高度,从而满足红黑树条件)。
删除左孩子情况:
- s为红; s染红,p染黑,左旋p。
- s为黑,LN与RN为黑; s染红,x回溯至p。
- s为黑,LN为红,RN为黑; LN染黑,s染红,右旋p。
- s为黑,LN随意,RN为红; s变为p的颜色,p和RN染黑,左旋p。
删除右孩子的情况和删除左孩子的情况相对称。
所有的情况为:

以删除左孩子为例,如下图,x为删除节点的后继节点。则p的左子树黑高度比右子树少1。若经过调整后,左右子树黑高恢复相等,则完成修复,否则,会转换为另一种情况,并按次方法继续进行修正。
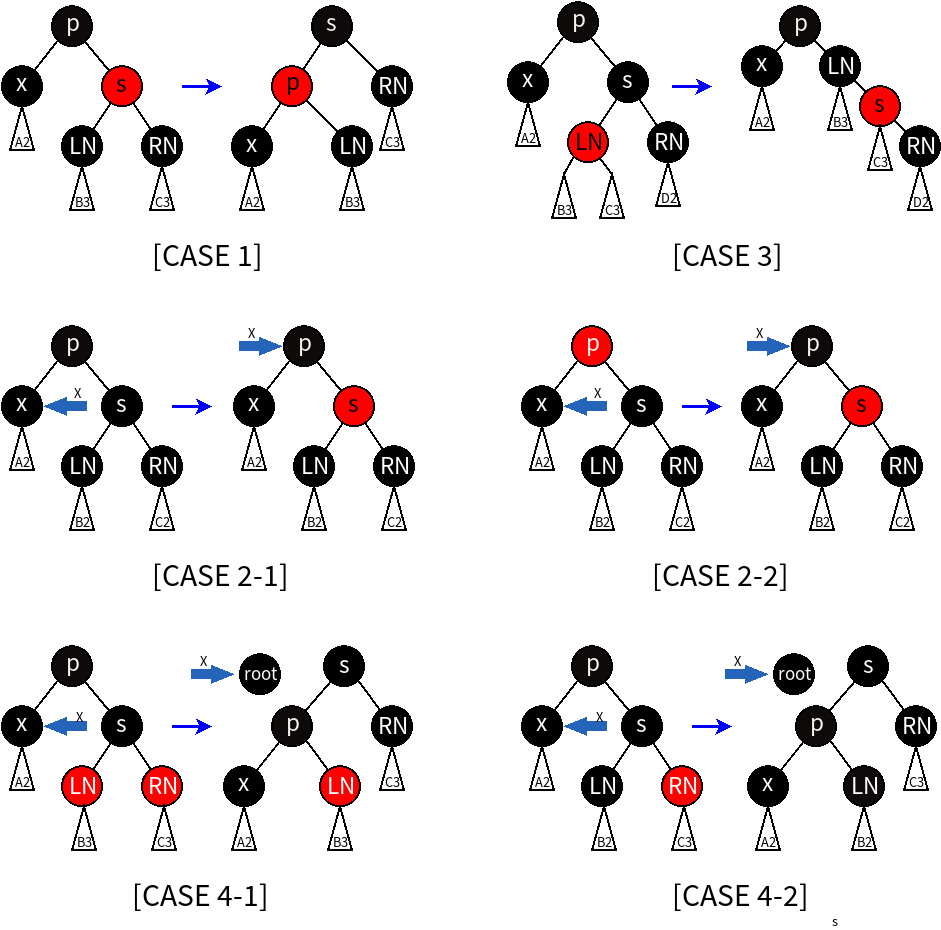
修正后情况的转换
情况转换的的原因:经调整后,左右子树的黑高度仍不相等,需要针对新的情况继续进行调整。
若修正后的左右子树黑高相同,则修正结束,无需情况转换。
转换如下:
Case 1 ==>> Case 2-2,Case 3,Case 4-1或 Case 4-2 不会引起黑高变化
Case 2-1 ==>> all Cases 当p为root节点时,会使整个树的黑高度减少1(唯一减少树黑高的情况)。
Case 2-2 ==>> redOver 并结束调整。
Case 3 ==>> Case 4-1或 Case 4-2;
Case 4 ==>> rootOver;
根据JDK源代码,分析函数对各种情况的处理方法。
private void fixAfterDeletion(TreeMap.Entry<K, V> var1) {
while(var1 != this.root && colorOf(var1)) {
//若当前节点为红色或者到达根节点,则修正结束。
TreeMap.Entry var2;
if (var1 == leftOf(parentOf(var1))) { //当前节点为左孩子
var2 = rightOf(parentOf(var1)); //兄弟节点s
if (!colorOf(var2)) { //s为红 [Case 1]
setColor(var2, true); //s染黑
setColor(parentOf(var1), false); //p染红
this.rotateLeft(parentOf(var1)); //左旋p
var2 = rightOf(parentOf(var1)); //更新兄弟s
}
if (colorOf(leftOf(var2)) && colorOf(rightOf(var2))) {
//LN 和 RN都为黑[Case 2]
//若从[Case 1]转换而来,则p为红[Case 2-2]
//但[Case 2]两种情况的处理策略相同
setColor(var2, false); //s染红
var1 = parentOf(var1); //x向上回溯
} else { //LN 和 RN不全黑 [Case 3,4]
if (colorOf(rightOf(var2))) { //RN黑[Case 3]
setColor(leftOf(var2), true);//LN染黑
setColor(var2, false); //s染红
this.rotateRight(var2); //右旋s
var2 = rightOf(parentOf(var1));//更新s为LN
}
//经[Case 3]修正后转换为[Case 4]
//[Case 4]分为两种情况,但修正方法相同
setColor(var2, colorOf(parentOf(var1)));//将s染成p的颜色
setColor(parentOf(var1), true); //p染黑
setColor(rightOf(var2), true); //RN染黑
this.rotateLeft(parentOf(var1)); //左旋p
var1 = this.root; //x回溯至根节点
//至此修正已基本完成(还有可能对根节点染黑)
}
} else {
//当前节点为左孩子,对称情况
var2 = leftOf(parentOf(var1)); //兄弟节点s
if (!colorOf(var2)) { //兄弟节点为红[Case 1]
setColor(var2, true); //s染黑
setColor(parentOf(var1), false); //p染红
this.rotateRight(parentOf(var1)); //p右旋
var2 = leftOf(parentOf(var1)); //更新s为LN
}
if (colorOf(rightOf(var2)) && colorOf(leftOf(var2))) {
//LN 和 RN都为黑[Case 2]
//若从[Case 1]转换而来,则p为红[Case 2-2]
//但[Case 2]两种情况的处理策略相同
setColor(var2, false); //s染红
var1 = parentOf(var1); //向上回溯
} else { //LN 和 RN不全黑 [Case 3,4]
if (colorOf(leftOf(var2))) { //LN黑,RN红[Case 3]
setColor(rightOf(var2), true);//RN染黑
setColor(var2, false); //s染红
this.rotateLeft(var2); //左旋s
var2 = leftOf(parentOf(var1));//更新s为LN
}
//经[Case 3]修正后转换为[Case 4]
//[Case 4]分为两种情况,但修正方法相同
setColor(var2, colorOf(parentOf(var1)));//s染成p的颜色
setColor(parentOf(var1), true); //p染黑
setColor(leftOf(var2), true); //LN染黑
this.rotateRight(parentOf(var1)); //右旋p
var1 = this.root; //x直接回溯到root
//至此修正已基本完成(还有可能对根节点染黑)
}
}
}
//根红色节点染黑,或者将根节点染黑
setColor(var1, true);
}
总结:
红黑树节点删除后的“双黑”现象修正,虽然情况复杂,情况间转换也复杂,但这些转换都是为了修正节点删除产生的叶节点黑深度不相等。而黑深度相等是红黑树的规定之一,红黑树的规定可以确保树中节点的高效插入,搜索和删除操作。这些努力都是为了实现数据结构的良好性能。
后记
学习红黑树的知识,始于阅读《STL源码剖析》中的第五章:关联式容器。关联式容器的底层数据结构是二叉搜索树,红黑树作为一种高效且通用的平衡二叉搜索树,被作为STL关联数据类的底层数据结构。在继续阅读关联是容器的源代码前,需要对红黑树有一个初步的认识。而且数据结构是高效算法的基石,也是STL的基础。
在学习红黑树的过程中,我看了网上的视频,作者是以JDK源代码进行讲解的。在阅读相关JDK源代码时,发现JDK源代码也很清晰明了,而且JDK里提供了丰富的容器类。相比之下,STL中提供的容器类就略显单一和老旧。但是阅读STL源码依然是学习程序语言,类层次结构设计,设计模式,数据结构和算法等知识的良好方法。而瞻仰JDK代码是今后的努力方向。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号