红黑树插入操作---以JDK 源码为例
红黑树遵循的条件:
1.根节点为黑色。
2.外部节点(叶子节点)为黑色。
3.红色节点的孩子节点为黑色。(由此,红色节点的父节点也必为黑色)
4.从根节点到任一外部节点的路径上,黑节点的数量相同。
节点插入过程
在红黑树中插入节点,首先调用查找接口,并在查找终止位置创建节点,并将节点染成红色。
当新插入节点的父节点为红色时,不满足红黑树的条件,产生‘双红’现象。此时,需要对树的拓扑结构和节点颜色进行调节。
双黑修正过程
以JDK TreeMap.class 中定义的红黑树类中插入修正函数为例,函数定义如下:
在这里约定插入节点为x,插入节点的父节点为p,祖父节点为g,曾祖父节点为gg,叔叔节点为u。双红修正根据插入节点周围的相关节点的不同情况,进行相应调整,分为以下几种情况:
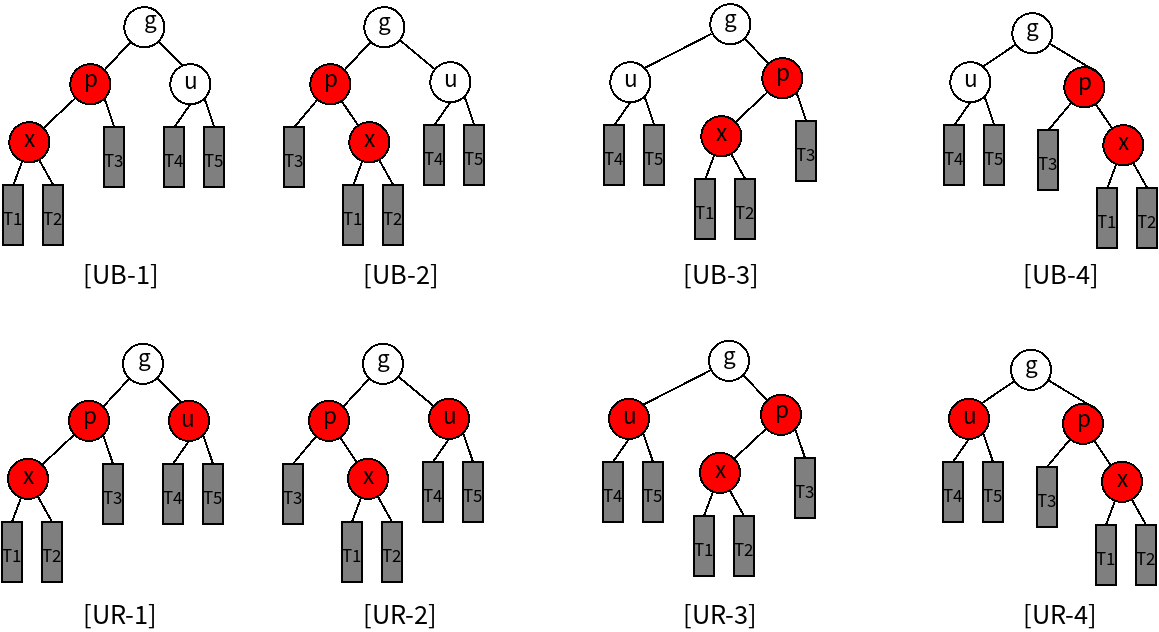
修正方法:
1.对于叔叔节点为黑色的情况[UB 1-4]
需要进行1至2次旋转(相当于进行3-4重构)。并对节点进行重新染色,使之满足红黑树约束条件,如下图所示。修正后该局部的最高节点为黑色,所以双红现象不会向上传播,因此,经过本步骤修正后即可使红黑树合法。
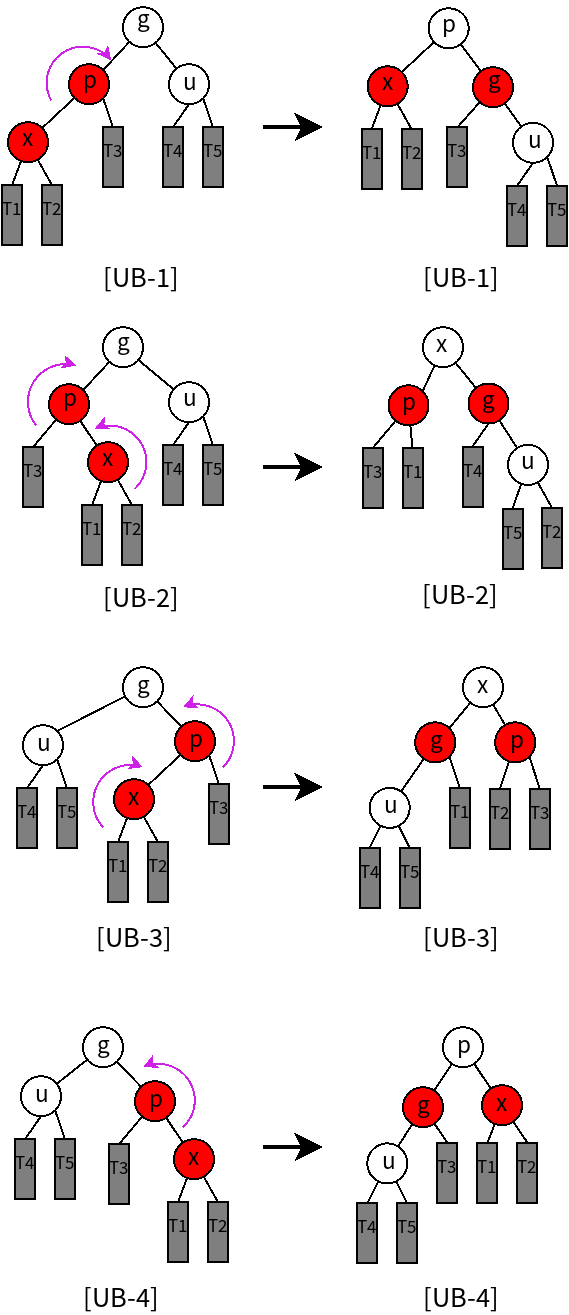
2.对于叔叔节点为红色的情况[UR 1-4]
无需要旋转,而仅需对插入节点及相关节点进行重新染色,使之满足红黑树约束条件,如下图所示。修正后该局部的最高节点变为红色,若曾祖父节点gg为红,则会产生新的双红现象,并可能依次向上传播,因此,需递归调用修正函数,继续向上修正,直到整个树合法。
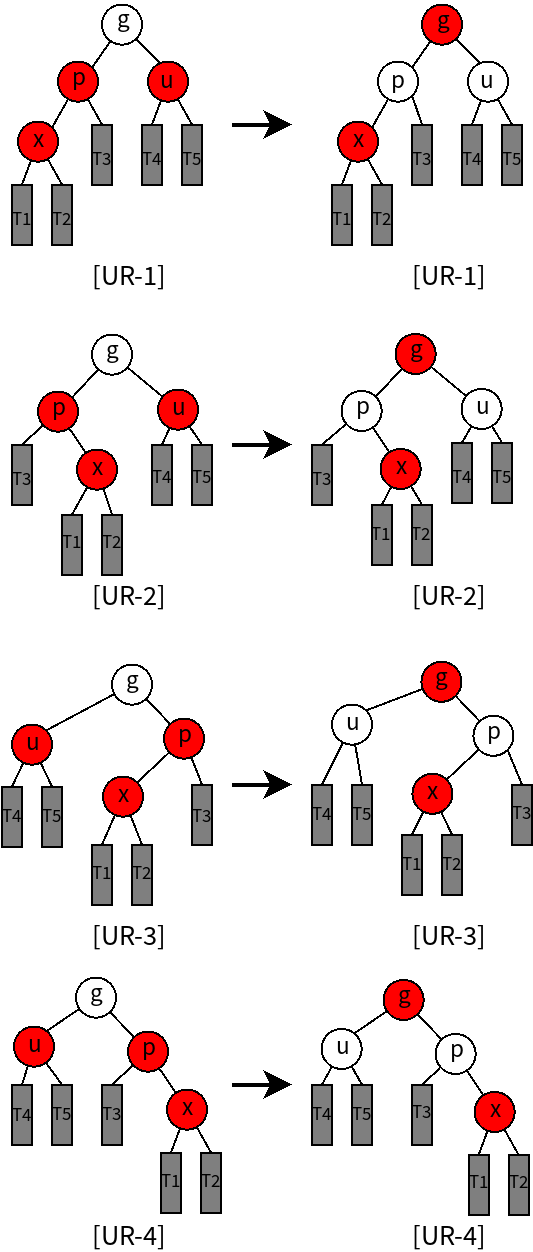
源码剖析
源代码路径/usr/lib/jvm/java-8-openjdk-amd64/jre/lib/rt.jar!/java/util/TreeMap.class (笔者使用的linux上的路径,具体路径根据安装位置会有所不同);
private void fixAfterInsertion(TreeMap.Entry<K, V> var1) {
var1.color = false; //节点颜色,true:黑色 false:红色
while(var1 != null && var1 != this.root && !var1.parent.color) {
//节点非空,非根节点,且父节点为红色 ==>>需要继续向上进行双红修正
TreeMap.Entry var2;
if (parentOf(var1) == leftOf(parentOf(parentOf(var1)))) {
//若插入节点的父节点p为祖父节点g的左孩子[UB-1,2][UR-1,2]
var2 = rightOf(parentOf(parentOf(var1))); //插入节点的叔叔节点U
if (!colorOf(var2)) { //叔叔节点为红色[UR-1,2]
setColor(parentOf(var1), true); //----重新染色----//
setColor(var2, true); //----重新染色----//
setColor(parentOf(parentOf(var1)), false); //----重新染色----//
var1 = parentOf(parentOf(var1)); //节点上升,准备向上修正
} else { //叔叔节点为黑色[UB-1,2]
if (var1 == rightOf(parentOf(var1))) { //插入节点x为右孩子 [UB-2]
var1 = parentOf(var1);
this.rotateLeft(var1); //先左旋
}
//插入节点x为右孩子 [UB-1]
setColor(parentOf(var1), true); //----重新染色----//
setColor(parentOf(parentOf(var1)), false); //----重新染色----//
this.rotateRight(parentOf(parentOf(var1))); //后右旋
}
} else {
//若插入节点的父节点p为祖父节点g的右孩子[UB-3,4][UR-3,4]
var2 = leftOf(parentOf(parentOf(var1))); //取得叔叔节点
if (!colorOf(var2)) { //叔叔节点为红色[UR-3,4]
setColor(parentOf(var1), true); //----重新染色----//
setColor(var2, true); //----重新染色----//
setColor(parentOf(parentOf(var1)), false); //----重新染色----//
var1 = parentOf(parentOf(var1)); //节点上升,准备向上修正
} else { //叔叔节点为黑色[UB-3,4]
if (var1 == leftOf(parentOf(var1))) { //插入节点x为左孩子[UB-3]
var1 = parentOf(var1); //
this.rotateRight(var1); //先右旋
}
//插入节点x为右孩子[UB-4]
setColor(parentOf(var1), true); //----重新染色----//
setColor(parentOf(parentOf(var1)), false); //----重新染色----//
this.rotateLeft(parentOf(parentOf(var1))); //左旋
}
}
}
this.root.color = true; //为避免将根节点染红,总是进行修正
}
当插入节点的叔叔节点为红色时[UR],需要将祖父节点g染红,从而可能导致双红现象向上传播(当gg为红时)。此时,需要递归调用双红修正函数,继续向上修正,直至消除树中双红现象。
在以上JDK代码中,并为出现函数递归调用,而是将递归调用更改为等价的迭代(while循环内)。在处理完叔叔节点为红的情况时,先进行染色,然后将当前节点x更新为其祖父节点g。在while循环内,持续进行修正。每循环一次,当将节点都会上升两层,直到到达根节点,或者gg为黑,修正即完成。
当x节点的祖父节点g为根节点时,而叔叔节点为红色时,修正函数会将根节点g染红,而违反红黑树规则1,此时,只需将根节点g染黑即可使红黑树恢复合法(函数最后一行),这也是唯一增加树的黑高度的情况。
笔者在阅读代码时,还产生一些疑惑:在[UB-2,3]两种情况的处理过程中,会更新当前节点x,如下所示。
[UB-2]
if (var1 == rightOf(parentOf(var1))) { //插入节点x为右孩子 [UB-2]
var1 = parentOf(var1);
this.rotateLeft(var1); //先左旋
}
[UB-3]
if (var1 == leftOf(parentOf(var1))) { //插入节点x为左孩子[UB-3]
var1 = parentOf(var1); //
this.rotateRight(var1); //先右旋
}
可以看到在旋转前,当前节点x会被替换为其父节点p,然后在对其进行旋转。来看一下旋转函数的定义:
private void rotateLeft(TreeMap.Entry<K, V> var1) {
if (var1 != null) {
TreeMap.Entry var2 = var1.right; //[1]
var1.right = var2.left; //[2]
if (var2.left != null) {
var2.left.parent = var1; //[3]
}
var2.parent = var1.parent; //[4]
if (var1.parent == null) {
this.root = var2; //[5]
} else if (var1.parent.left == var1) {
var1.parent.left = var2; //[6]
} else {
var1.parent.right = var2; //[6']
}
var2.left = var1; //[7]
var1.parent = var2; //[8]
}
}
函数中各步骤用图表达为:
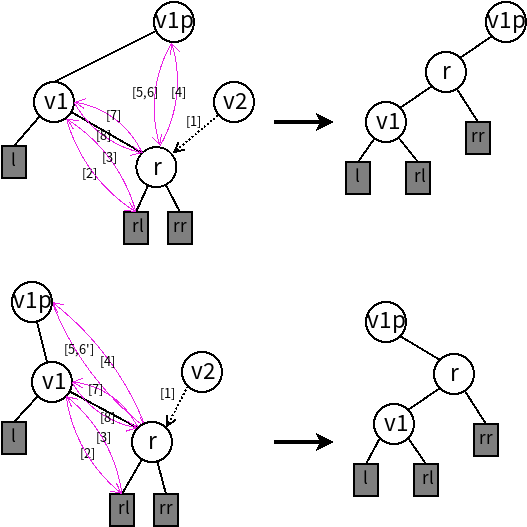
设x为当前节点x_old,其在fixAfterInsertion中被上升到父节点x=p,对x调用rotateLeft后,x的高度将降低一层,与原来的旧值x_old处于同一层次。这样在后续进行右旋或左旋时,即可对不同层次进行正确的染色。
以上图为例,若节点v1p为根节点,则节点r的原深度为3,在fixAfterInsertion中被上升到父节点r=p后,r的深度为2,在对r调用rotateLeft后,r的深度恢复为3,此后再对r调用parentOf后,即可得到深度为2的父节点,对r调用parentOf-parentOf后,得到深度为1的祖父节点,从而确保不同层次的节点被正确染色。右旋的情况左旋相类似。
由此可以得出结论:在对节点x进行旋转前,先将其指向父节点p,然后实施旋转,此后进行的染色即可和只需要一次旋转的操作保持一致性,使代码更加紧凑。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号