np.sum()函数详解

首先：sum()如果不传参就是对所有元素求和。

1、sum函数可以传入一个axis的参数，这个参数怎么理解呢？这样理解：

　　假设我生成一个numpy数组a，如下

>>> import numpy as np
>>> a = np.array([[[1,2,3,2],[1,2,3,1],[2,3,4,1]],[[1,0,2,0],[2,1,2,0],[2,1,1,1]]])
>>> a
array([[[1, 2, 3, 2],
        [1, 2, 3, 1],
        [2, 3, 4, 1]],
 
       [[1, 0, 2, 0],
        [2, 1, 2, 0],
        [2, 1, 1, 1]]])
>>> 

　　这是一个拥有两维的数组，每一维又拥有三个数组，这个数组里面拥有四个元素。如果我们要将这个a数组中的第一个元素1定位出来，则我们会输入a[0][0][0]。好，这个axis的取值就是这个精确定位某个元素需要经过多少数组的长度，在这里是3，所以axis的取值有0，1，2。如果一个数组精确到某个元素需要a[n0][n1][n2][...][n]，则axis的取值就是n。定位 到这里，axis的参数的取值就解释完成了。

2 、理解参数axis取值对sum结果的影响：

　　前面说了axis的取值（以数组a为例），axis=0，1，2。在这里，精确定位到某个元素可以用a[n0][n1][n2]表示。n0的取值是0，1（数组两维），代表第一个索引；n1的取值是0，1，2（每一维数组拥有3个子数组），代表第二个索引；n2的取值是0，1，2，3（每个子数组有4个元素），代表第三个索引，这几个取值在后面会用到。

2.1、axis = 0的时候：

　　axis=0，对应n0已经确定下来，即n0取值定为0，1。所以sum每个元素的求和公式是sum = a[0][n1][n2]+a[1][n1][n2]。接下来确定sum的行数和列数，n1的取值是0，1，2，为3个数，代表行数，n2的取值是0，1，2，3，为4个数，代表列数，所以sum为3*4的数组。

      如何求sum的各个元素呢，sum = a[0][n1][n2]+a[1][n1][n2]这个公式又如何理解呢？如下。我们可以做一个表格：注意颜色

 

 

 　　所以sum(axis=0)的值是 [ [2, 2, 5, 2], [3, 3, 5, 1], [4, 4, 5, 2]]。

　　验证一下, 正确！

>>> a.sum(axis=0)
array([[2, 2, 5, 2],
       [3, 3, 5, 1],
       [4, 4, 5, 2]])

 2.2、axis = 1的时候：

　　axis=1，对应n1已经确定下来，即n1取值定为0，1，2。所以sum每个元素的求和公式是sum =a[n0][0][n2]+a[n0][1][n2]+a[n0][2][n2]。接下来确定sum的行数和列数，n0的取值是0，1，为2个数，代表行数，n2的取值是0，1，2，3，为4个数，代表列数，所以sum为2*4的数组。

　　如何求sum的各个元素呢，sum = a[n0][0][n2]+a[n0][1][n2]+a[n0][2][n2]这个公式又如何理解呢？我们又做一个表格，颜色不标注了

 

 

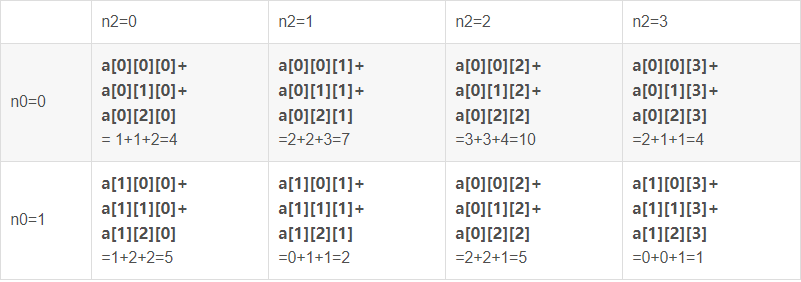
 所以sum(axis=1)的值是 [ [4, 7, 10, 4], [5, 2, 5, 1]]。验证如下，正确。

>>> a.sum(axis=1)
array([[ 4,  7, 10,  4],
       [ 5,  2,  5,  1]])

2.3 axis = 2的时候：     

　　axis=2，对应n2已经确定下来，即n2取值定为0，1，2, 3。所以sum每个元素的求和公式是sum =a[n0][n1][0]+a[n0][n1][1]+a[n0][n1][2]+a[n0][n1][3]。接下来确定sum的行数和列数，n0的取值是0，1，为2个数，代表行数，n1的取值是0，1，2，为3个数，代表列数，所以sum为2*3的数组。

　　如何求sum的各个元素呢，sum = a[n0][n1][0]+a[n0][n1][1]+a[n0][n1][2]+a[n0][n1][3]这个公式又如何理解呢？我们又做一个表格，颜色不标注了

　　所以sum(axis=2)的值是 [ [8, 7, 10], [3, 5, 5]]. 验证如下，正确。

>>> a.sum(axis=2)
array([[ 8,  7, 10],
       [ 3,  5,  5]])

————————————————
版权声明：本文为CSDN博主「rifengxxc」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/rifengxxc/article/details/75008427